Population genetics of rapid adaptation and the predictability of evolution


Richard Neher
MPI for Developmental Biology


slides at neherlab.org/201701_vienna.html

Evolution of HIV


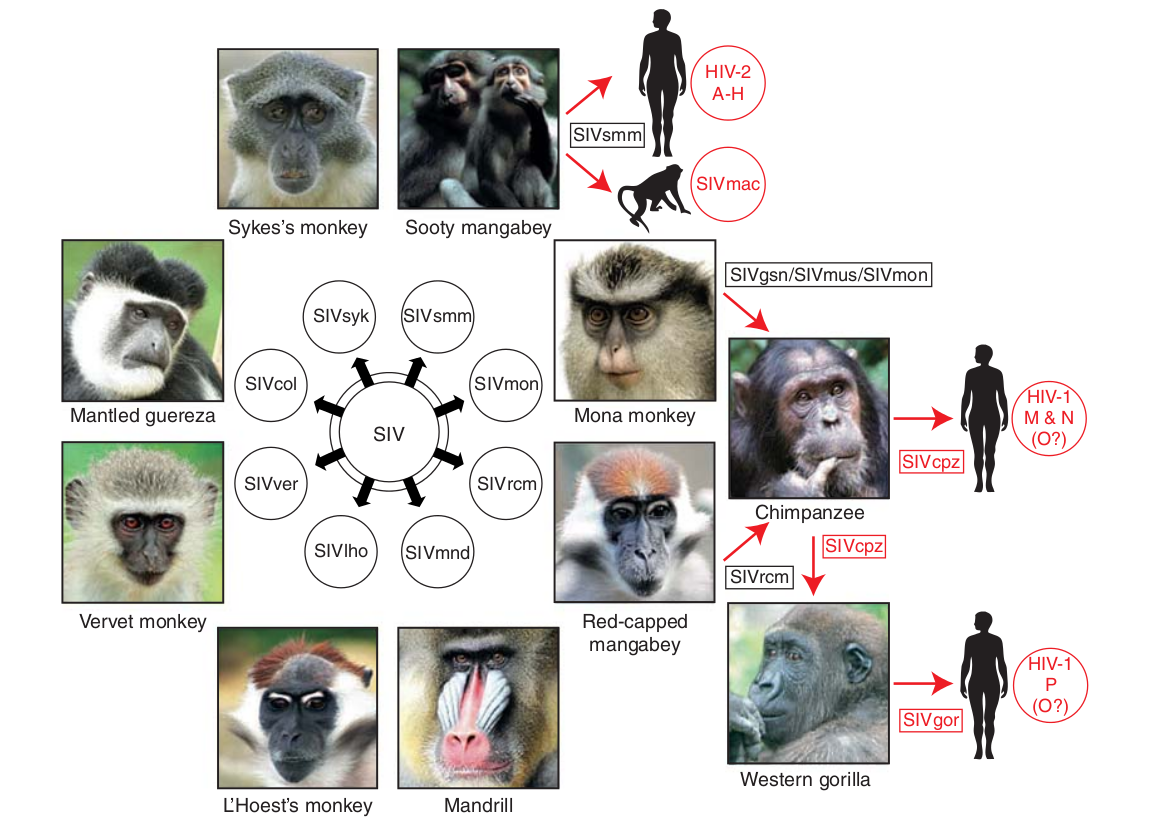
  • Chimp → human transmission ~1900 gave rise to HIV-1 group M
  • Diversified into subtypes that are ~20% different
  • evolves at a rate of about 0.1% per year
image: Sharp and Hahn, CSH Persp. Med.


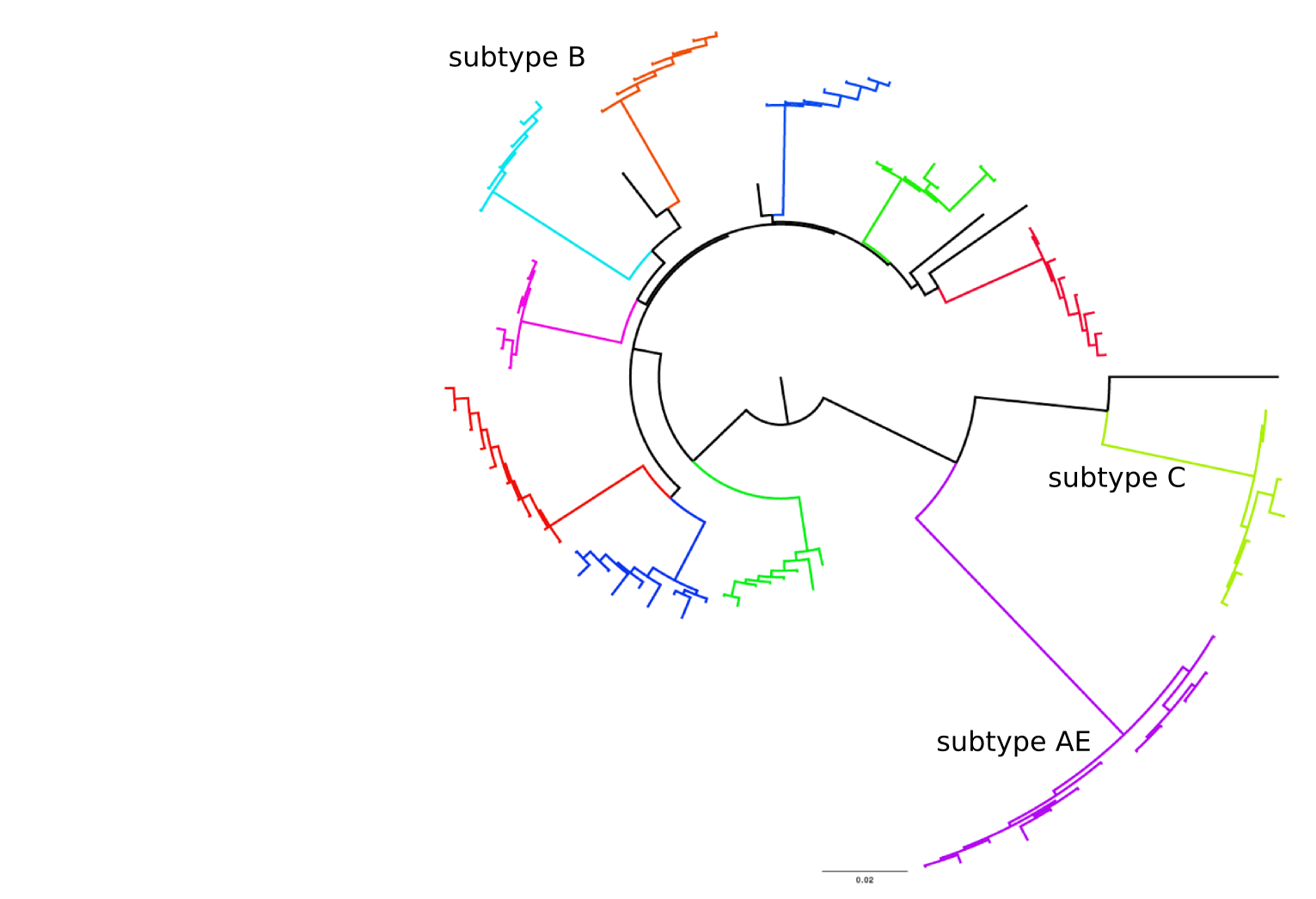
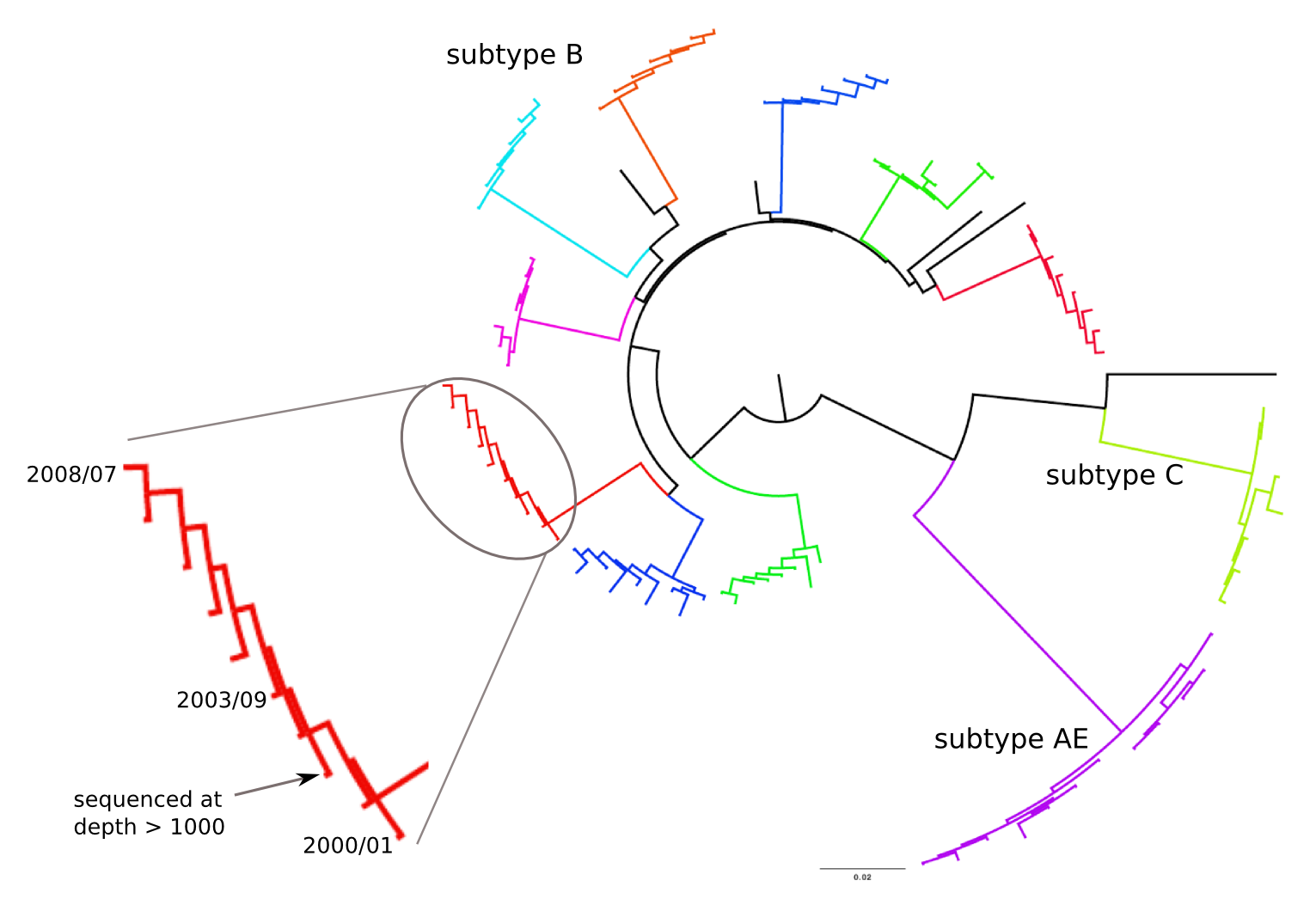
Population sequencing to track all mutations above 1%

  • diverge at 0.1-1% per year
  • almost full genomes coverage in 10 patients
  • full data set at hiv.tuebingen.mpg.de
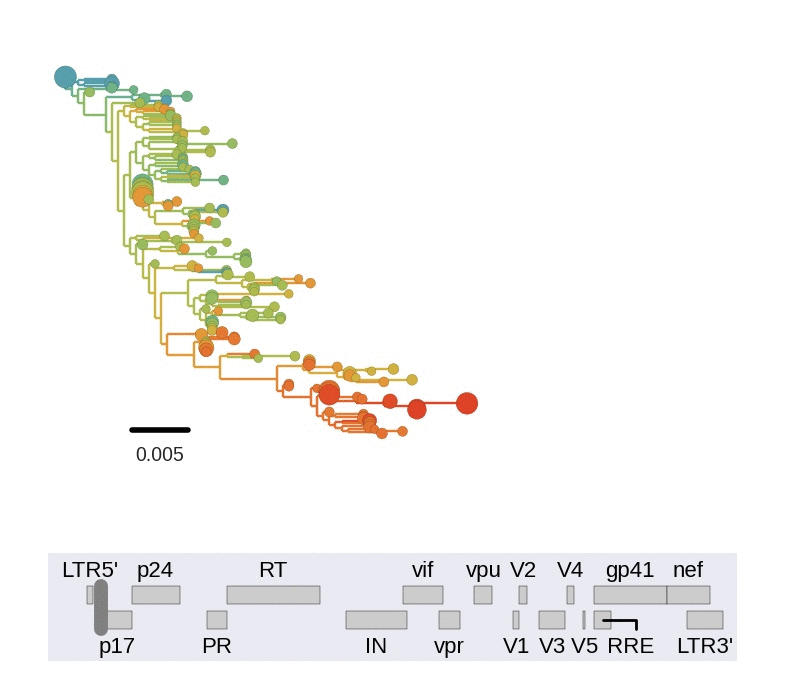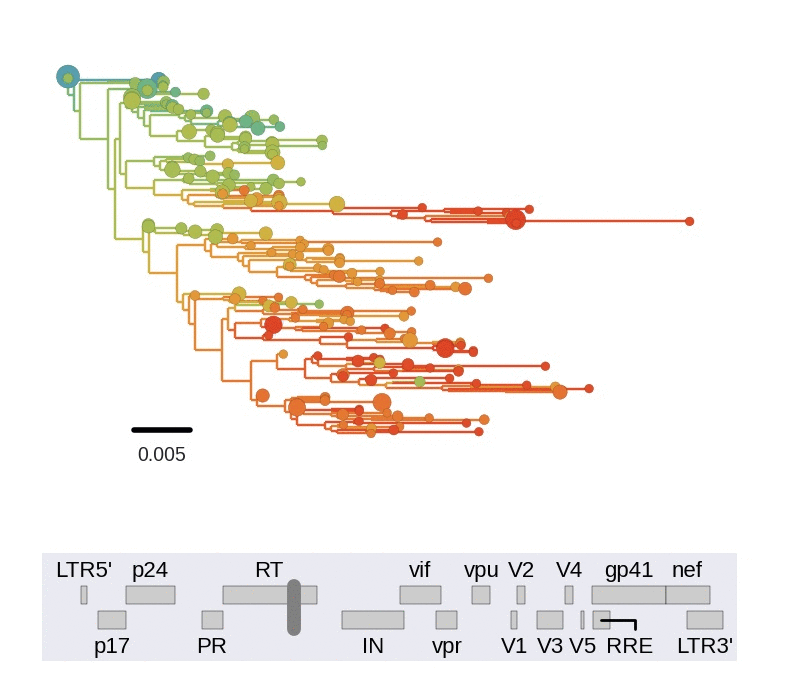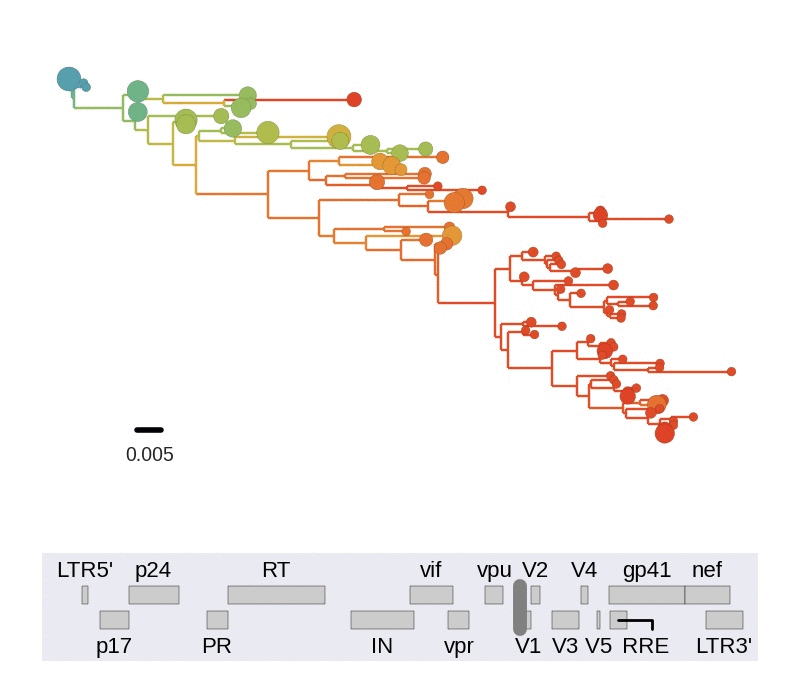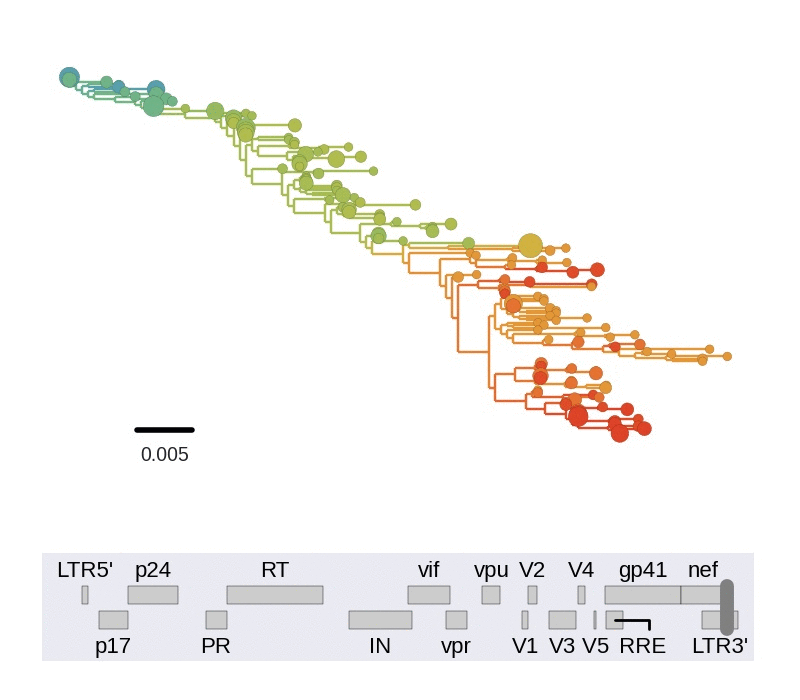
Zanini et al, eLife, 2015; antibody data from Richman et al, 2003

Diversity and hitchhiking

  • envelope changes fastest, enzymes lowest
  • identical rate of synonymous evolution
  • diversity saturates where evolution is fast
  • synonymous mutations stay at low frequency
Zanini et al, eLife, 2015

Frequent version of previously beneficial mutations

  • HIV escapes immune systems
  • most mutations are costly
  • humans selects for different mutations
  • are there costs compensated or reverted
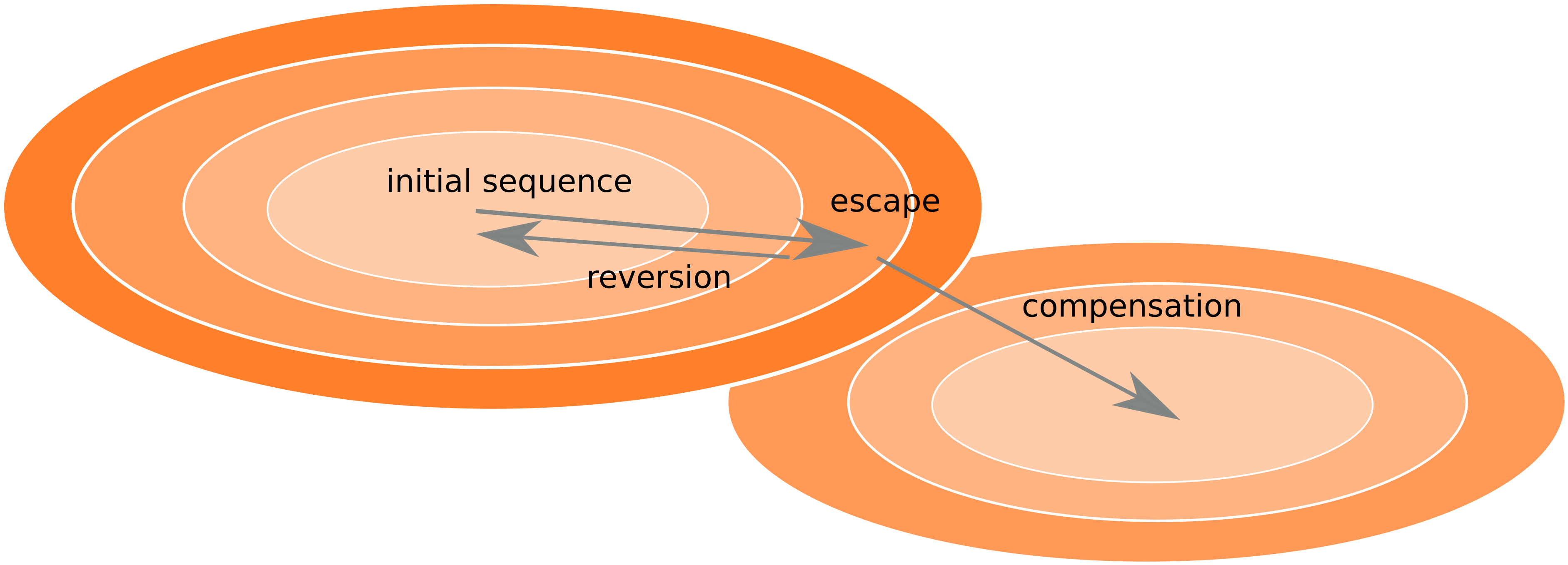
  • Almost one third of all mutations are reversions vs expected: 5%
  • Strong evolutionary attractor
Zanini et al, eLife, 2015

Fitness landscape of HIV-1

Zanini et al, biorxiv, 2017

Selection on RNA structures and regulatory sites

Zanini et al, biorxiv, 2017

The distribution of fitness effects

Zanini et al, biorxiv, 2017

Population genetics models

evolutionary processes ↔ trees ↔ genetic diversity

Neutral models and beyond

Neutral models
  • all individuals are identical → same offspring distribution
  • Kingman coalesence and diffusion theory are dual descriptions
  • everything is easy to calculate
  • perturbations like background selection can be included

What if selection is everywhere?

Clonal interference and traveling waves

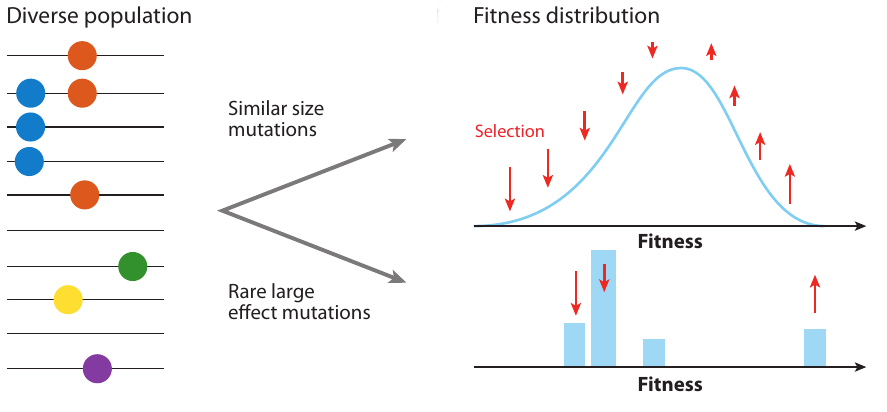
  • extensive work on speed of adaptation, but this speed is not observable
  • genetic diversity is what we observe
  • depends on the properties of trees

What if selection is everywhere?
RN, Annual Reviews, 2013

Kingman coalescent

strong selection

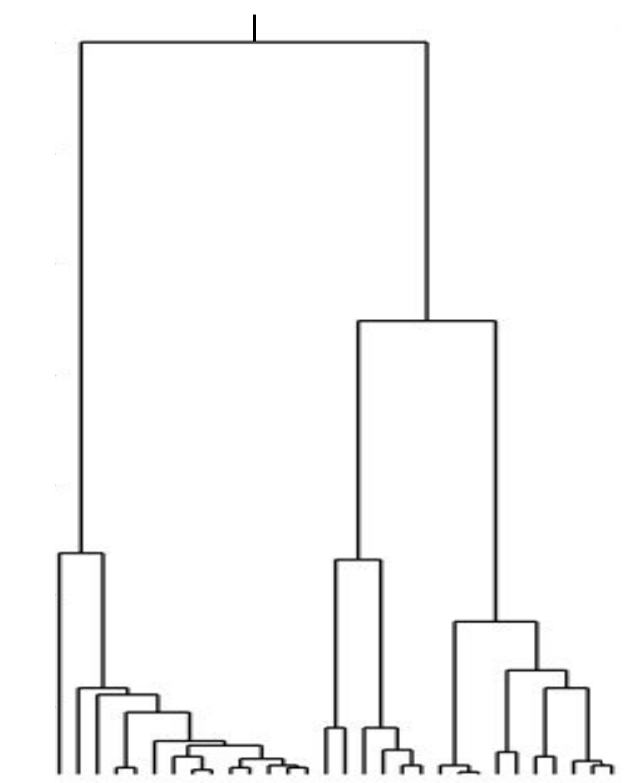
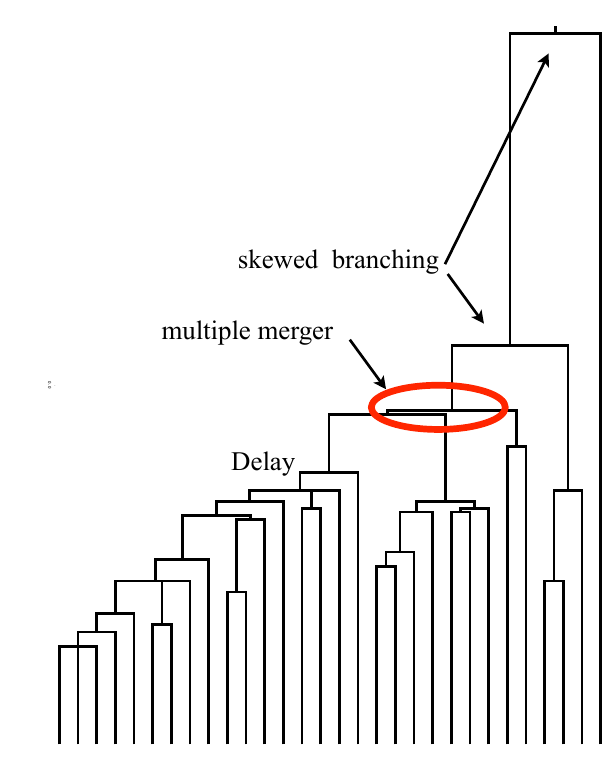
Bolthausen-Sznitman Coalescent

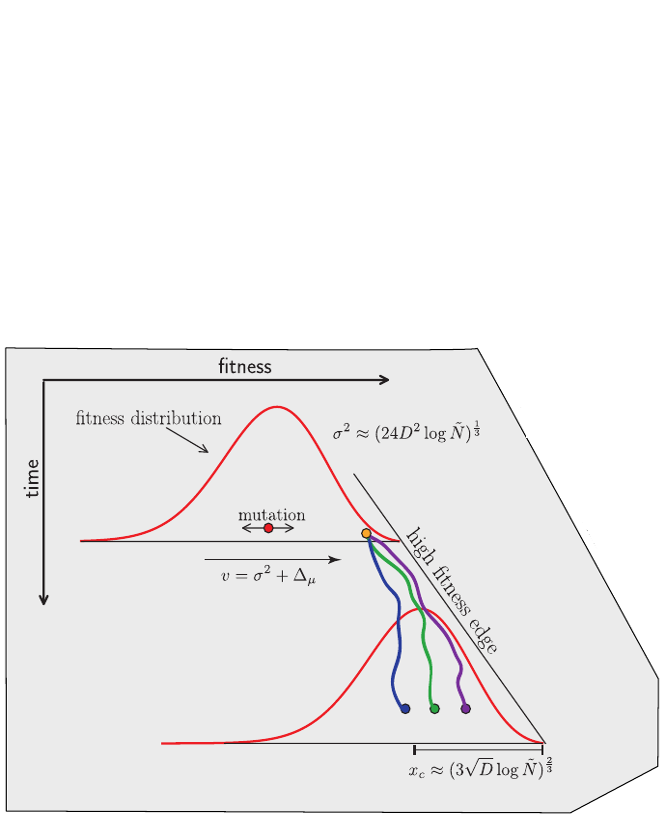
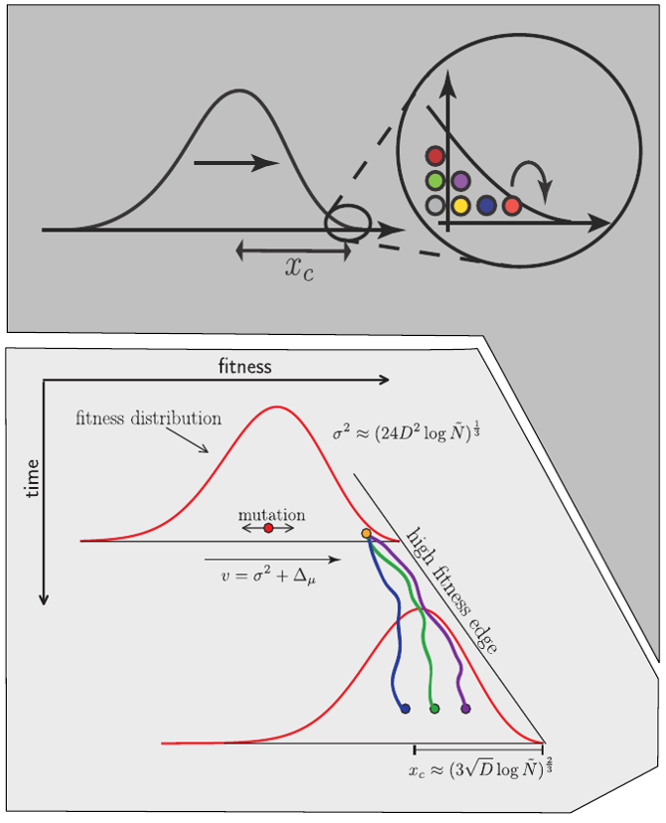
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007

Universality of the Bolthausen-Sznitman Coalescent (BSC)


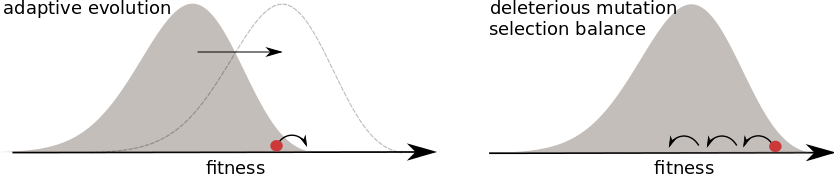
  • many small effect mutations → coalescence is BSC like
  • fitness diversity $\sigma$, not population size determines $T_{MRCA}$
  • the time scale of coalescence is always $T_c \sim \sigma^{-1}\sqrt{\log N}$
  • frequency dynamics is not diffusive, but has Levy-flight properties
  • Can be extended to sexual populations
Kosheleva, Desai; Desai, Walczak, Fisher, Genetics, 2013; RN, Hallatschek, PNAS, 2013, RN, Kessinger, Shraiman PNAS, 2013

U-shaped polarized site frequency spectra



RN, Hallatschek, PNAS, 2013
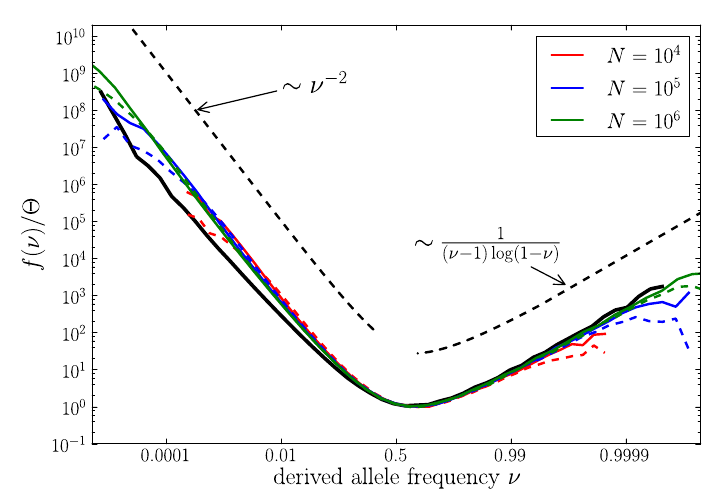
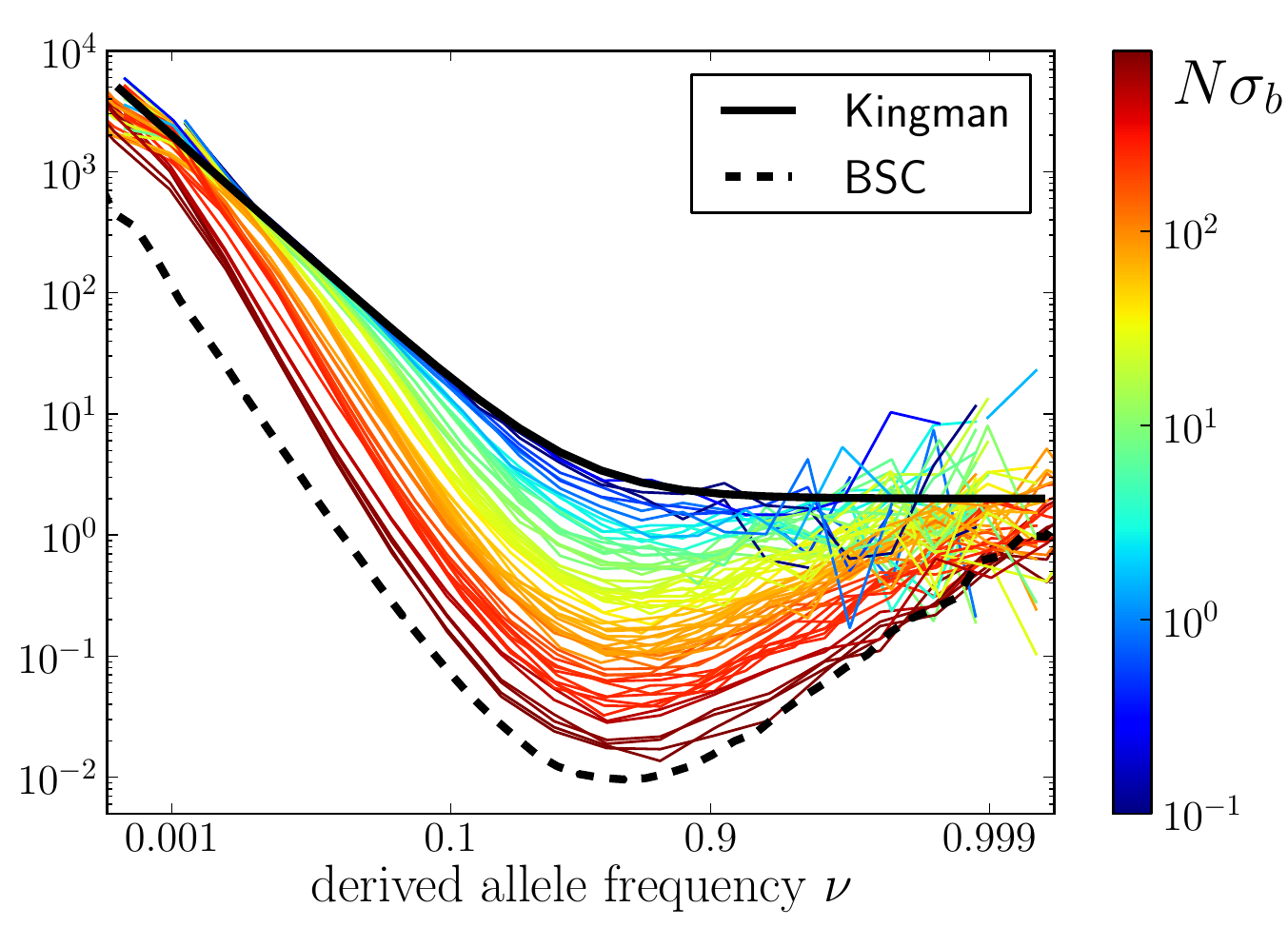RN, Kessinger, Shraiman, PNAS, 2013
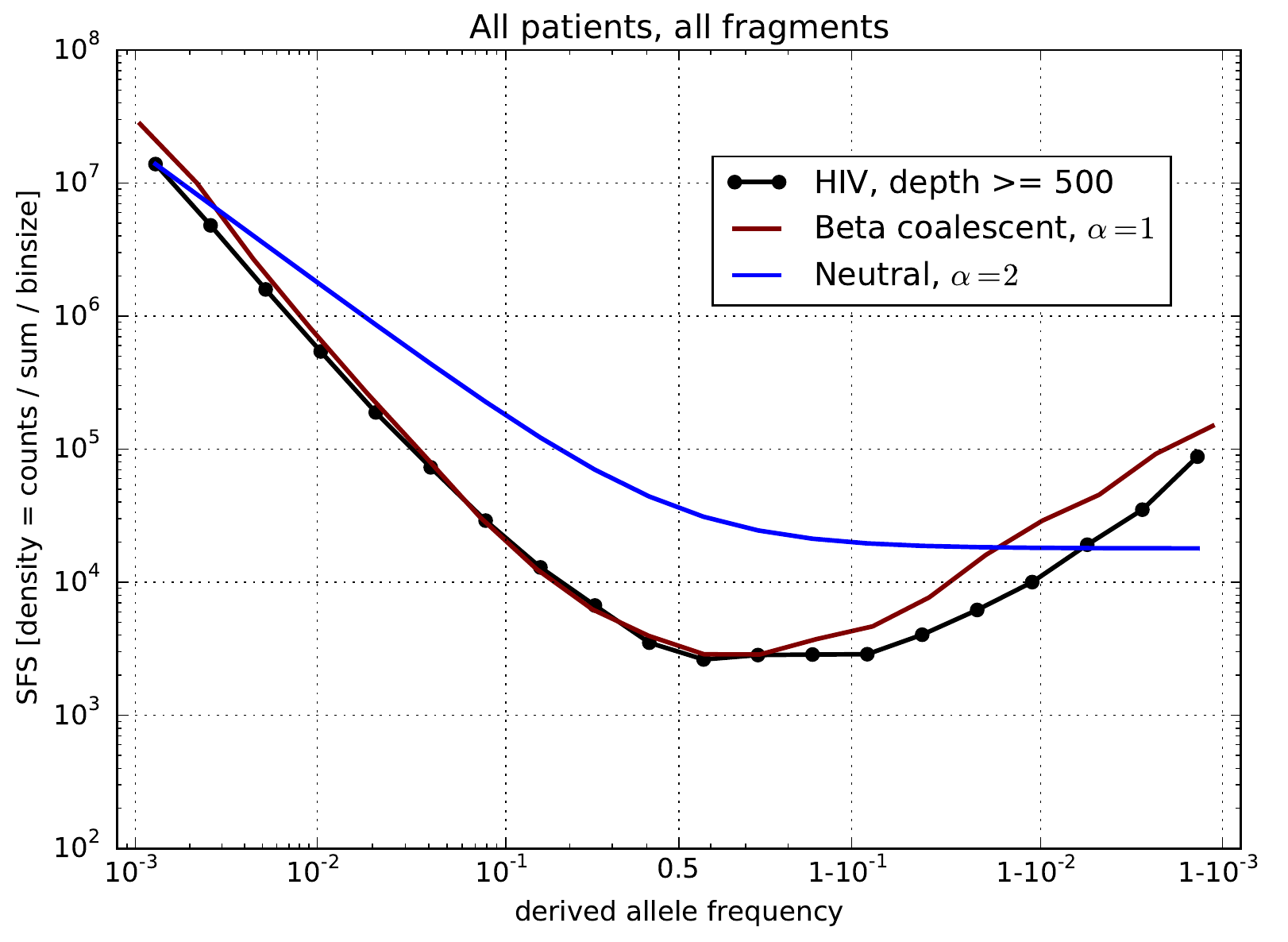Zanini et al, eLife, 2015

Bursts in a tree ↔ high fitness genotypes

Can we read fitness of a tree?




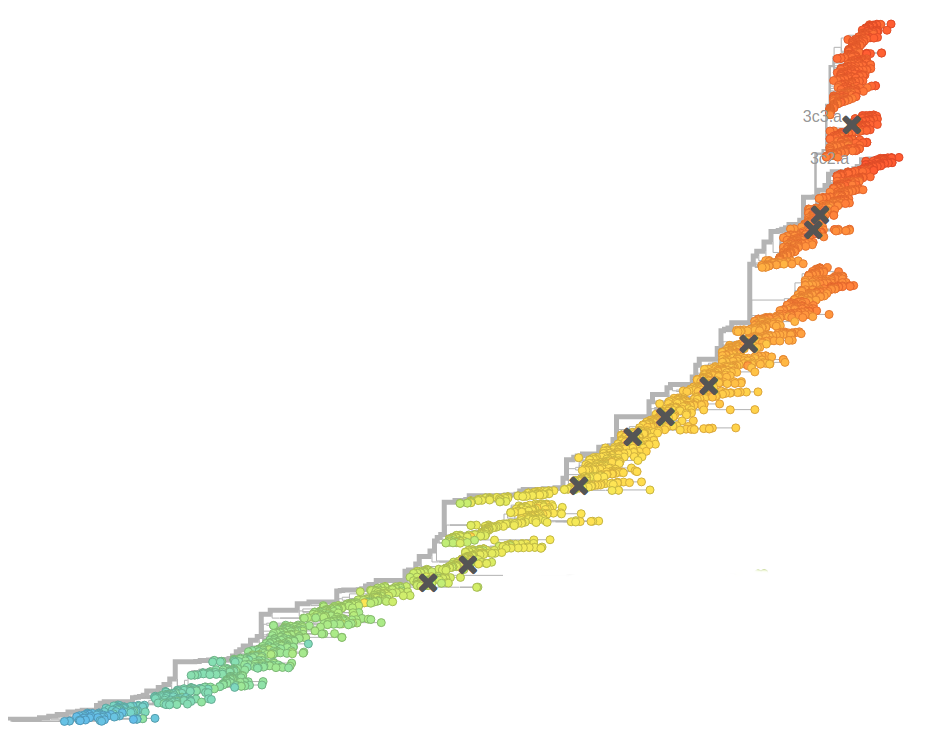
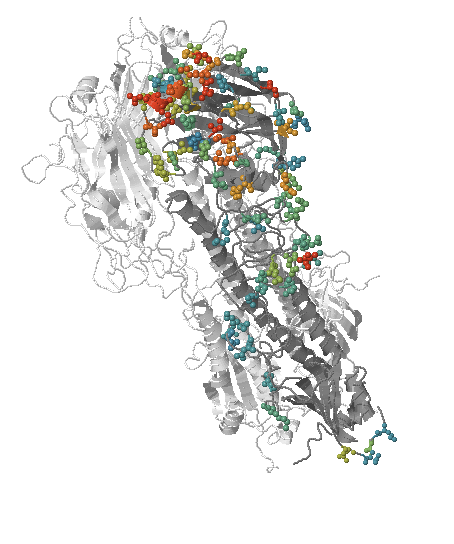
  • Influenza virus evolves to avoid human immunity
  • Vaccines need frequent updates

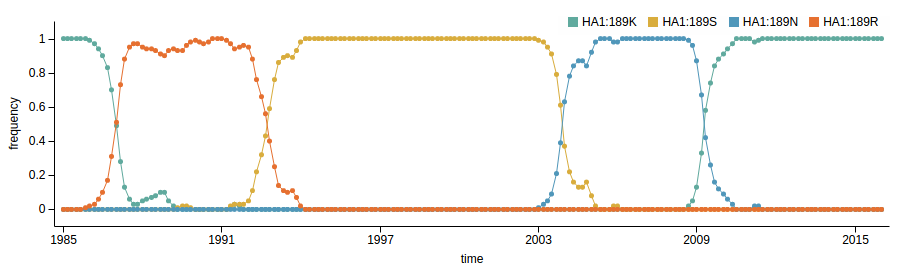
Predicting evolution

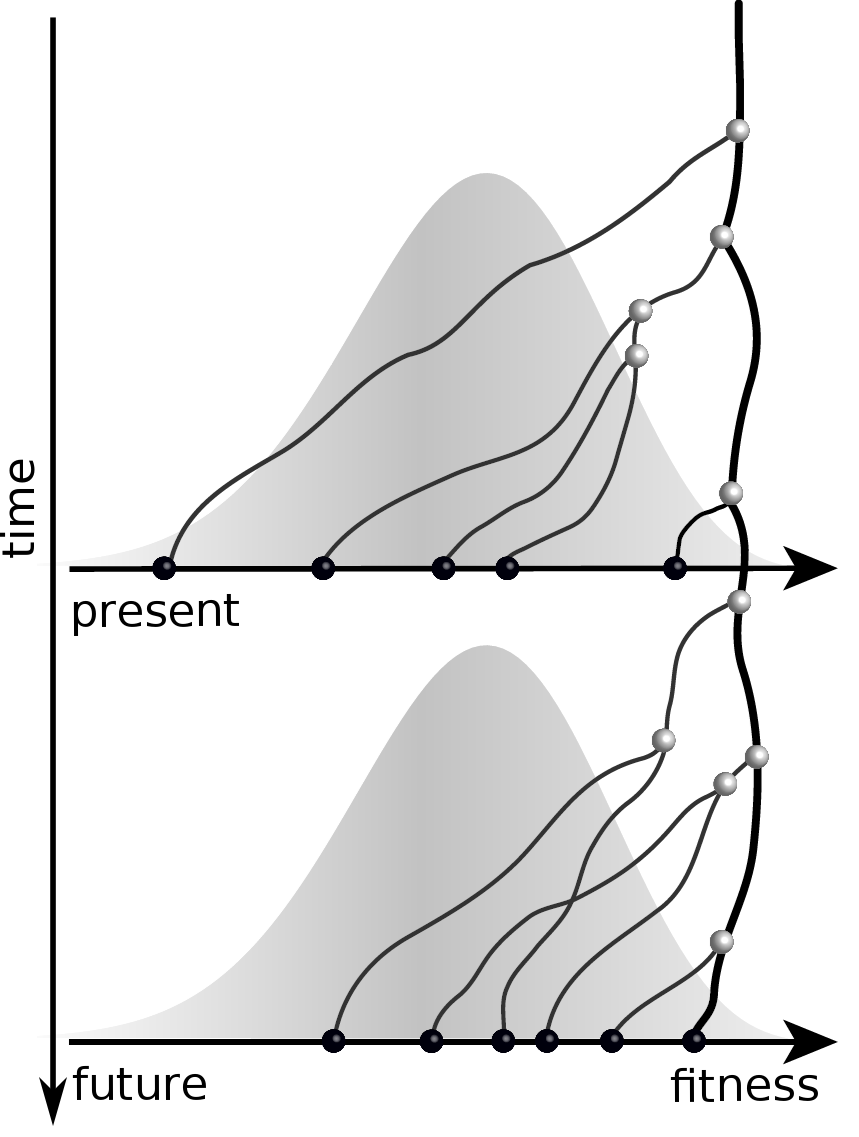
Given the branching pattern,
  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014

Validate on simulation data

  • simulate evolution
  • sample sequences
  • reconstruct trees
  • infer fitness
  • predict ancestor of future
  • compare to truth
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014
nextflu.org

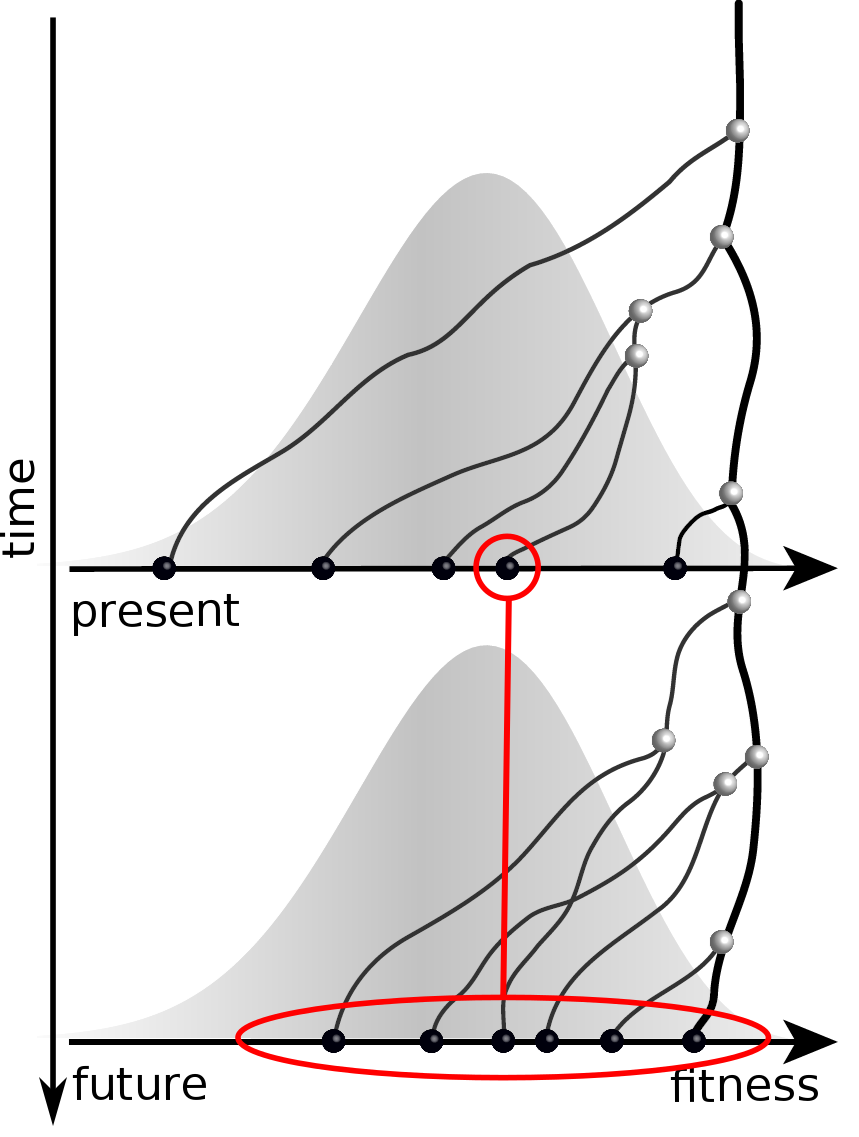
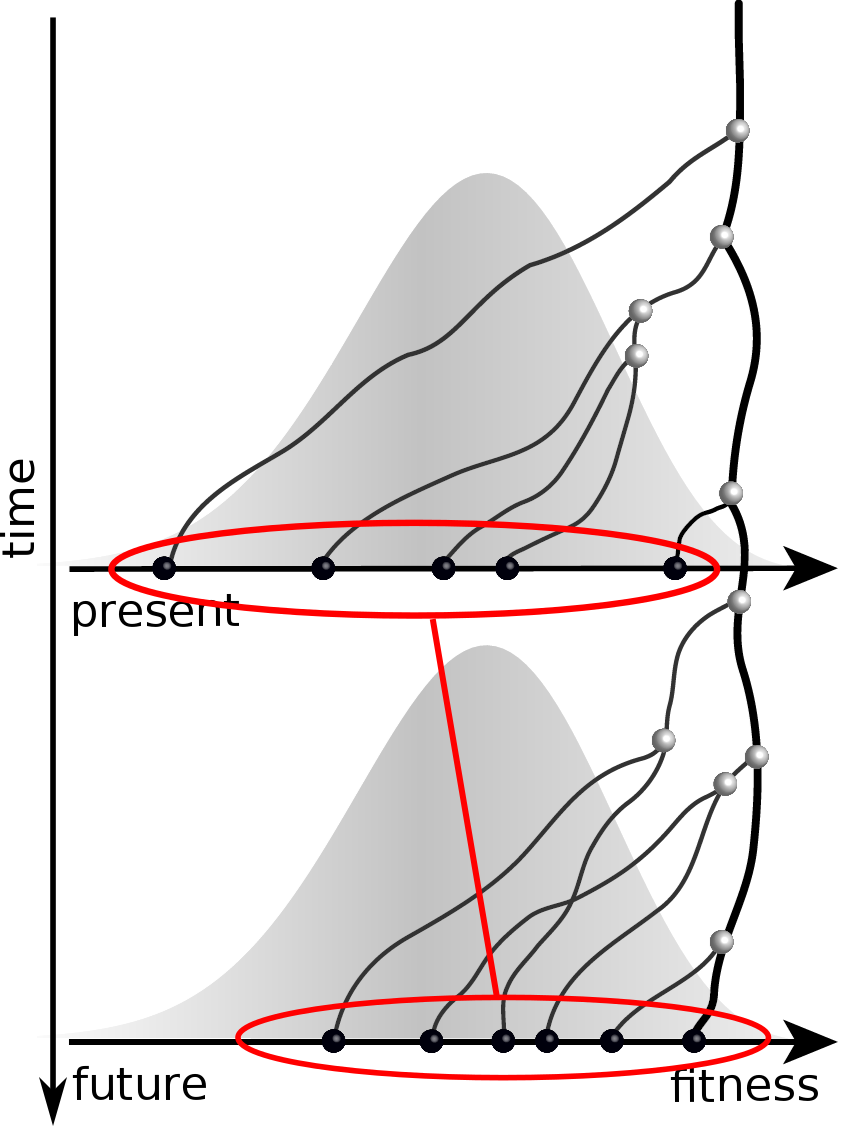
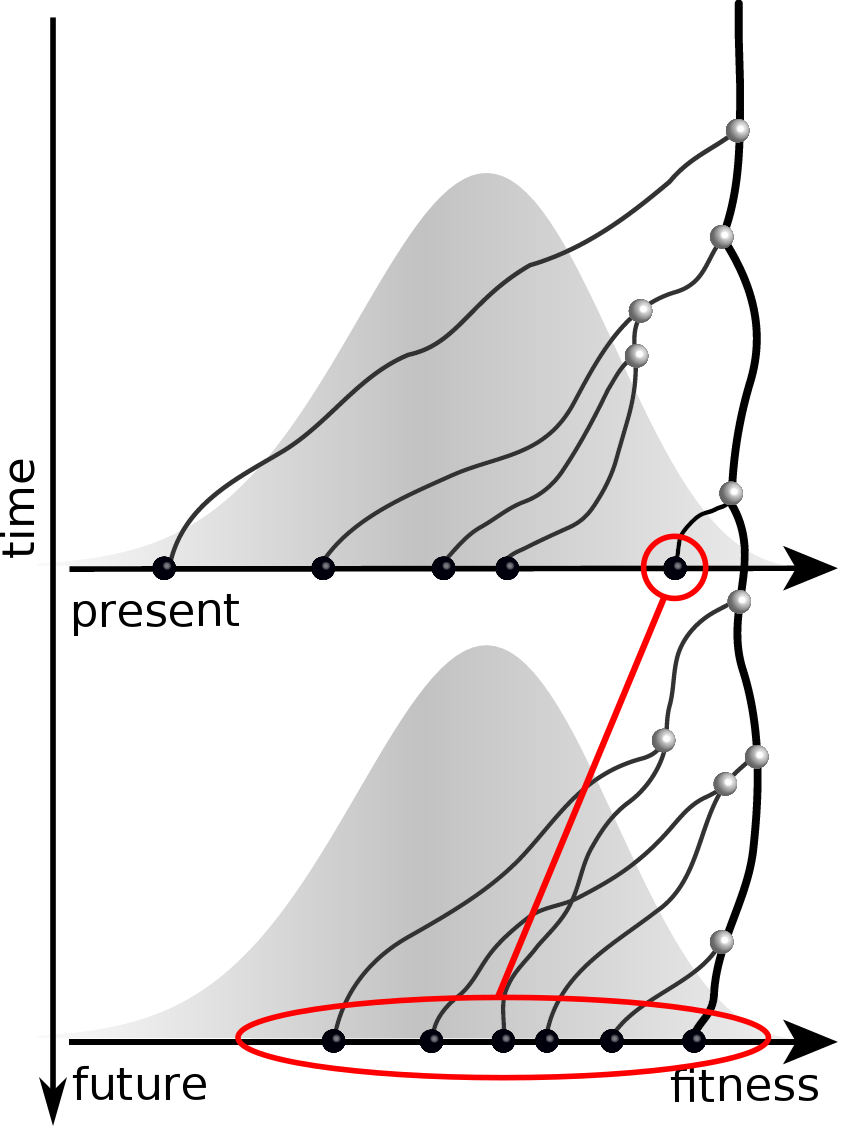
Prediction of the dominating H3N2 influenza strain

RN, Russell, Shraiman, eLife, 2014

HIV acknowledgments

  • Fabio Zanini
  • Jan Albert
  • Johanna Brodin
  • Christa Lanz
  • Göran Bratt
  • Lina Thebo

Influenza and Theory acknowledgments

  • Boris Shraiman
  • Colin Russell
  • Trevor Bedford
  • Oskar Hallatschek

My lab will move to the Biozentrum Basel

We will have post-doc openings!

get in touch!