Virus evolution and the predictability of next year's flu


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/201706_IGC_Lisbon.html

Evolution of HIV


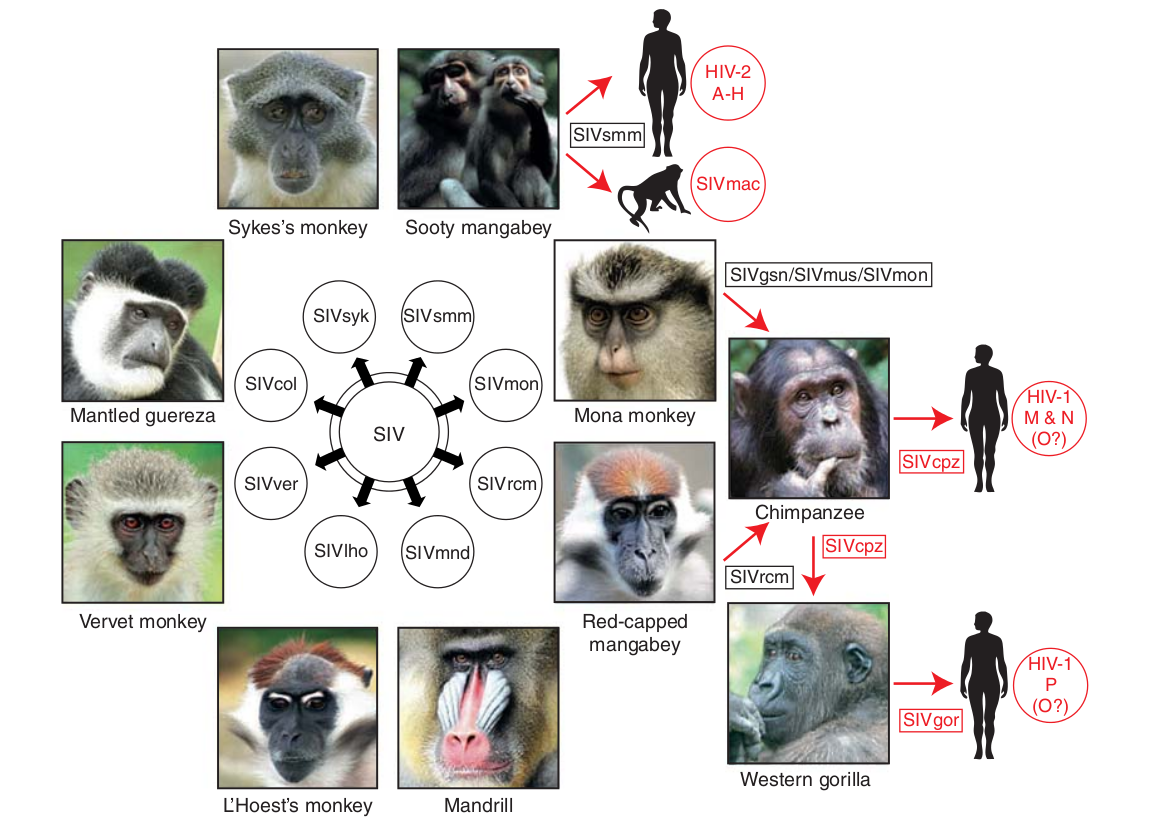
  • Chimp → human transmission ~1900 gave rise to HIV-1 group M
  • Diversified into subtypes that are ~20% different
  • evolves at a rate of about 0.1% per year
image: Sharp and Hahn, CSH Persp. Med.

HIV infection

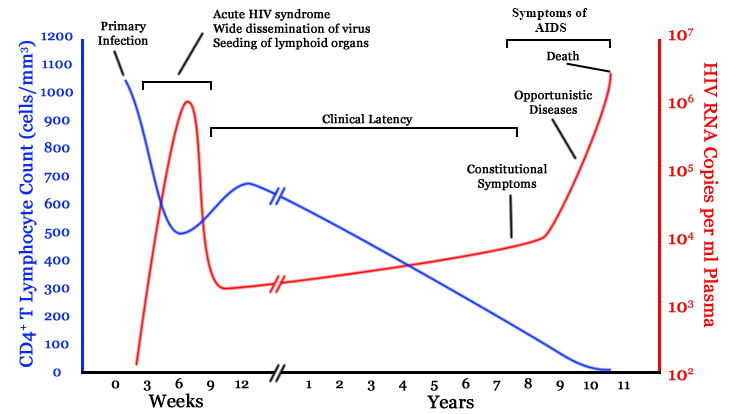chronic infection:
  • $10^8$ cells are infected every day
  • the virus repeatedly escapes immune recognition
  • integrates into T-cell as latent provirus
 image: wikipedia

HIV replication cycle

image: wikipedia

HIV-1 evolution within one individual



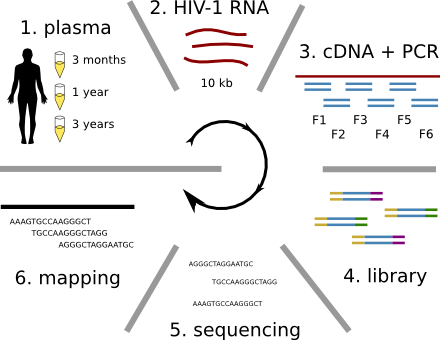
silouhette: clipartfest.com, Zanini at al, 2015. Collaboration with Jan Albert and his group

HIV-1 sequencing before and after therapy

Zanini et al, eLife, 2015; Brodin et al, eLife, 2016


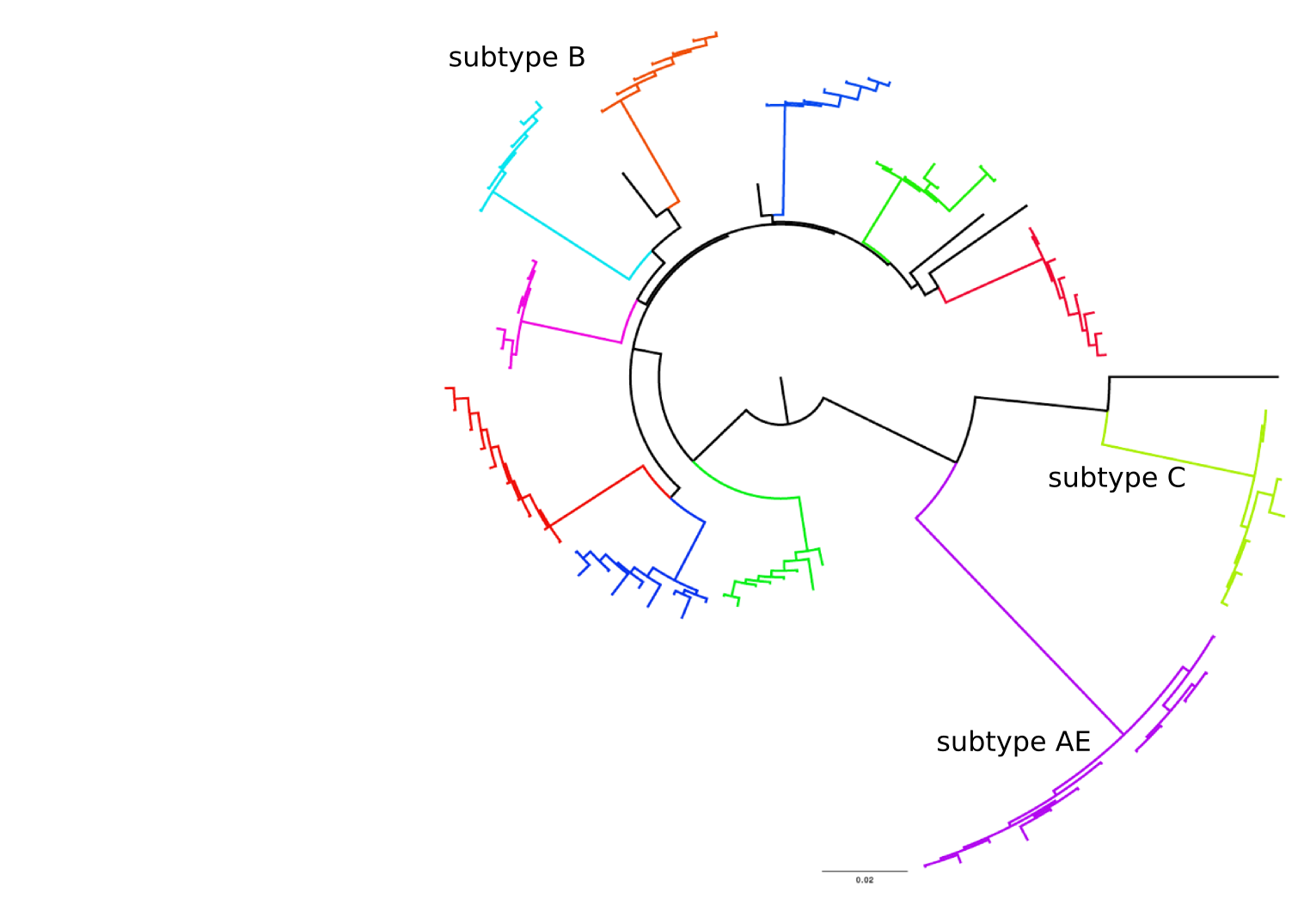
Population sequencing to track all mutations above 1%

Zanini et al, eLife, 2015; antibody data from Richman et al, 2003

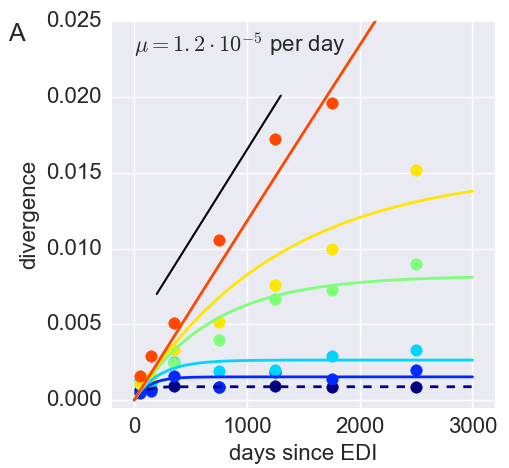
Diversity and mutation rates

  • envelope changes fastest, enzymes lowest
  • identical rate of synonymous evolution
  • diversity saturates where evolution is fast
  • synonymous mutations stay at low frequency
Zanini et al, eLife, 2015

Mutation rates and diversity and neutral sites

Zanini et al, Virus Evolution, 2017

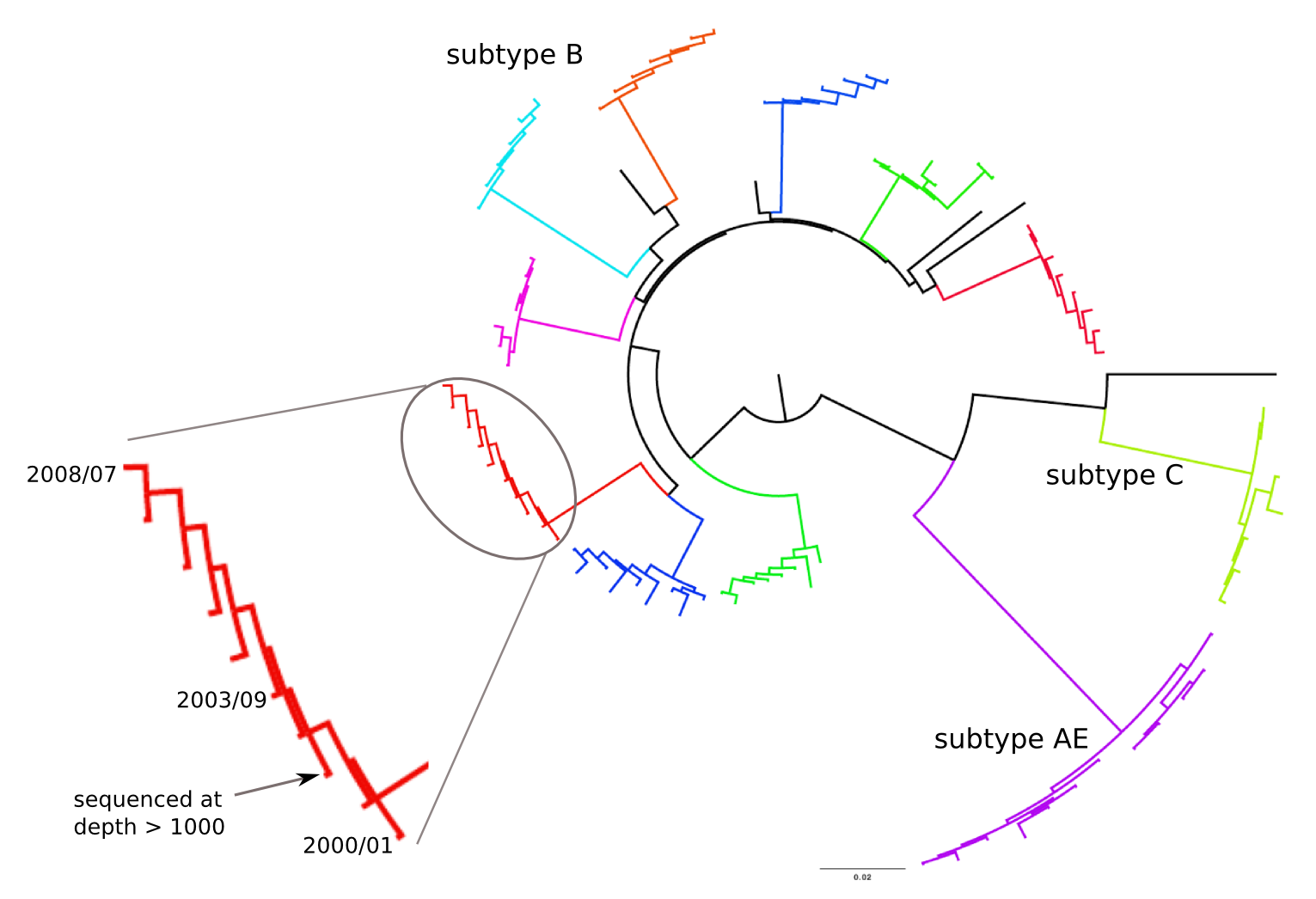
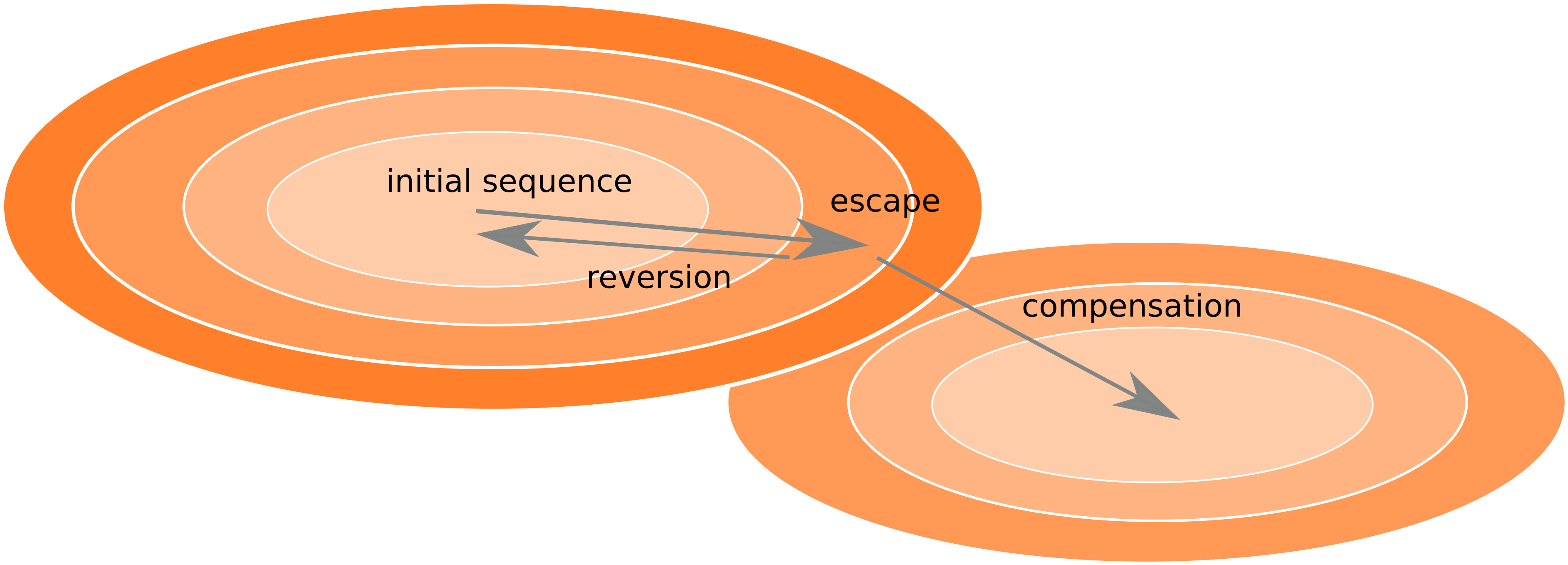
Frequent version of previously beneficial mutations

  • HIV escapes immune systems
  • most mutations are costly
  • humans selects for different mutations
  • compensation or reversion?
Zanini et al, eLife, 2015

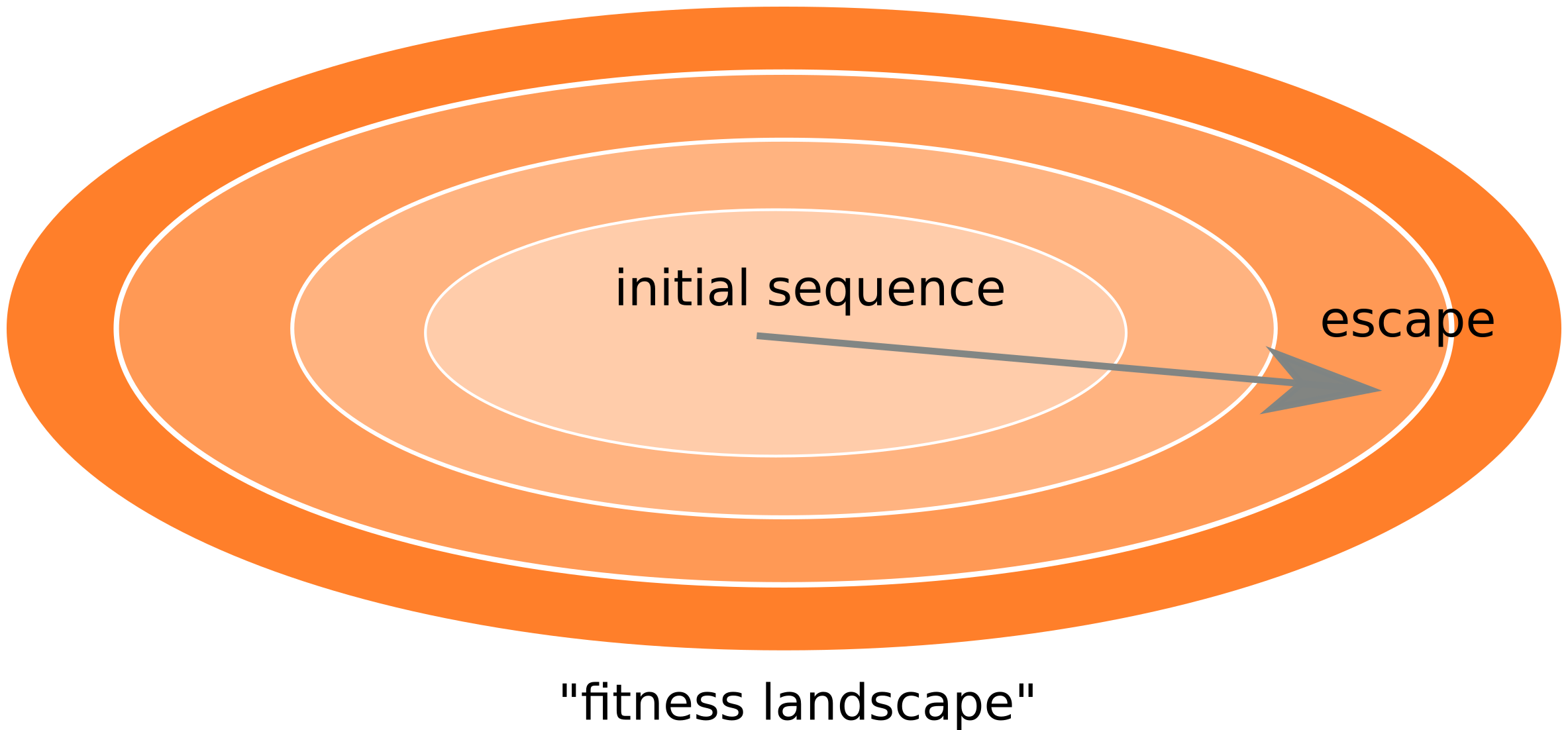
Inference of fitness costs

  • mutation away from preferred state at rate $\mu$
  • selection against non-preferred state with strength $s$
  • variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
  • equilibrium frequency: $\bar{x} = \mu/s $
  • fitness cost: $s = \mu/\bar{x}$
Zanini et al, Virus Evolution, 2017

Fitness landscape of HIV-1

Zanini et al, Virus Evolution, 2017

Selection on RNA structures and regulatory sites

Zanini et al, Virus Evolution, 2017

The distribution of fitness effects

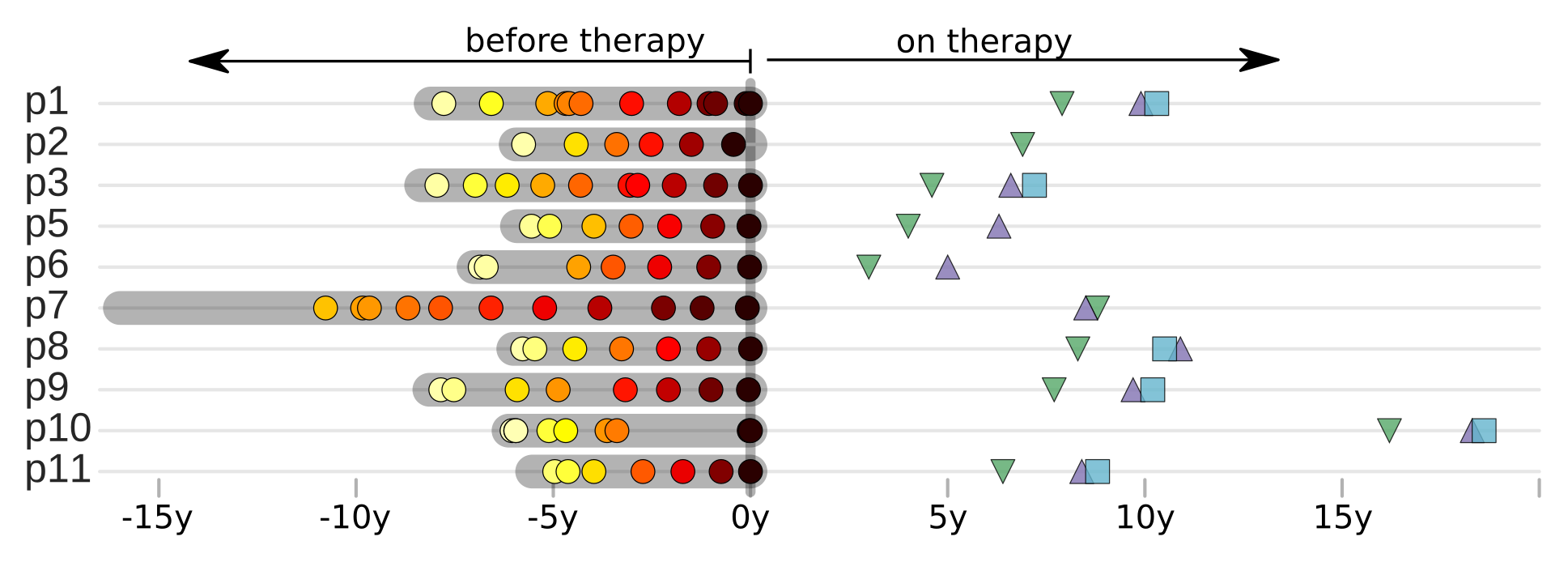
Zanini et al, Virus Evolution, 2017

Does HIV evolve during therapy?

Brodin et al, eLife, 2016

No evidence of ongoing replication

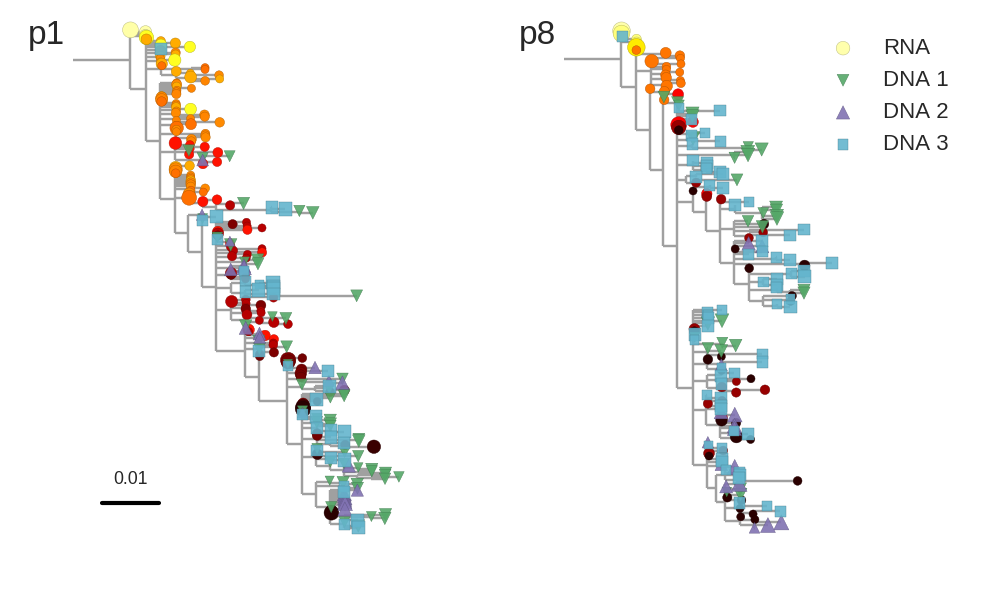
  • HIV-1 RNA from plasma before treatment started
  • HIV-1 DNA gag-p17 from PBMCs after many years of treatment
Brodin et al, eLife, 2016

No evidence of ongoing replication

Brodin et al, eLife, 2016

T-cell turnover is fast in untreated infection

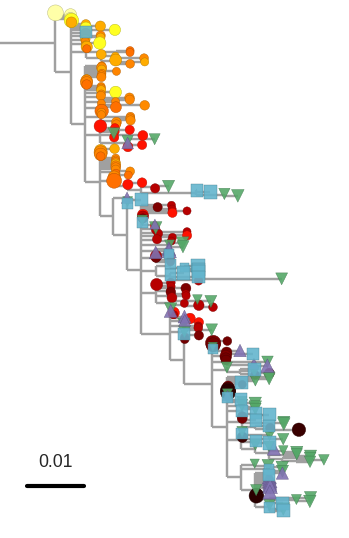
  • latent HIV → barcode of a T-cell lineage
  • all latent integrated virus derives from late infection
  • untreated: T-cell lineages are short lived
  • on therapy: T-cell clones live decades
Brodin et al, eLife, 2016

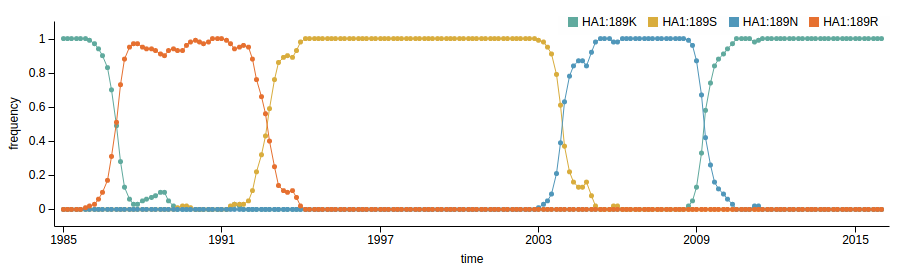
Human seasonal influenza viruses

slide by Trevor Bedford



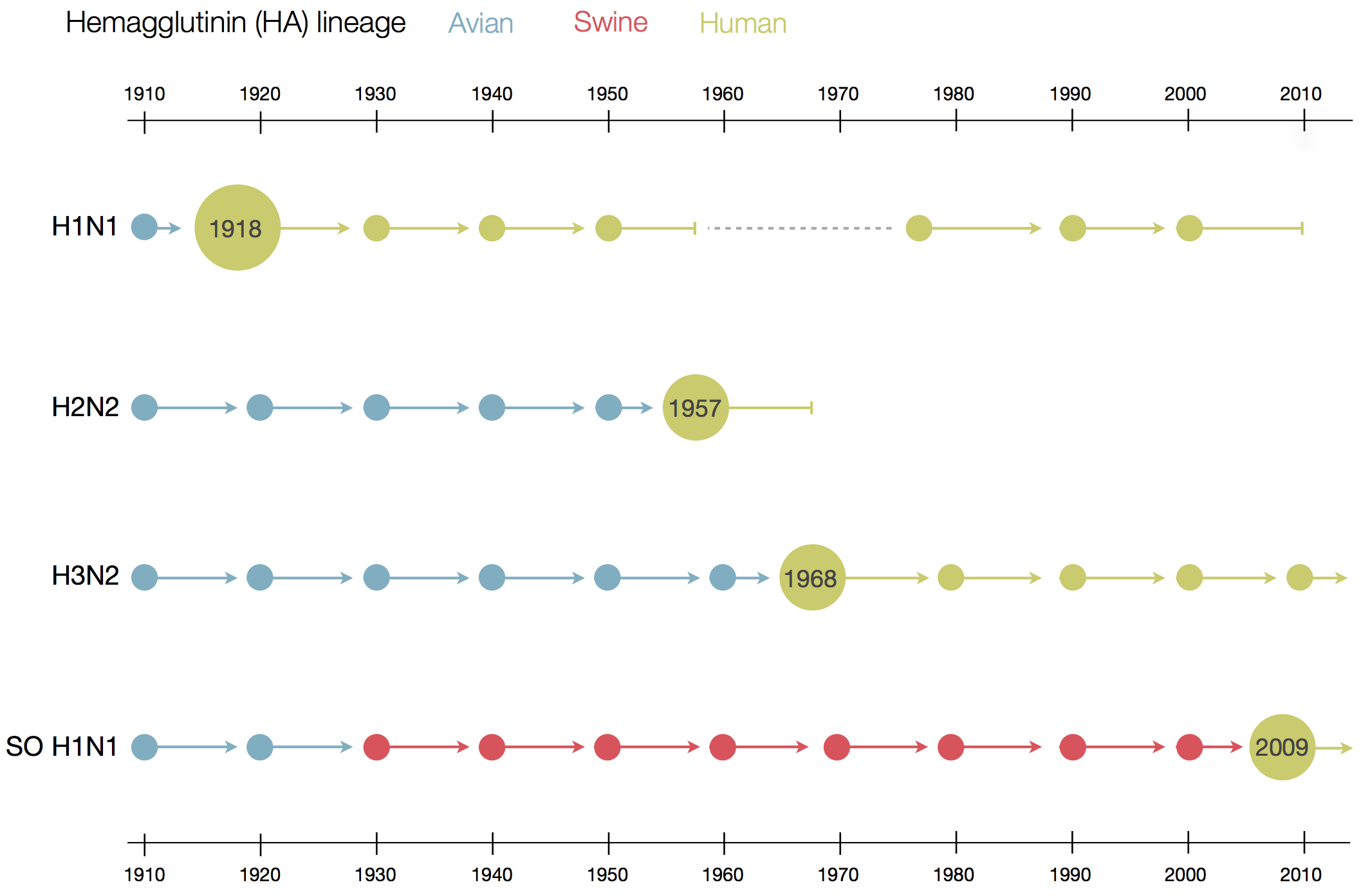
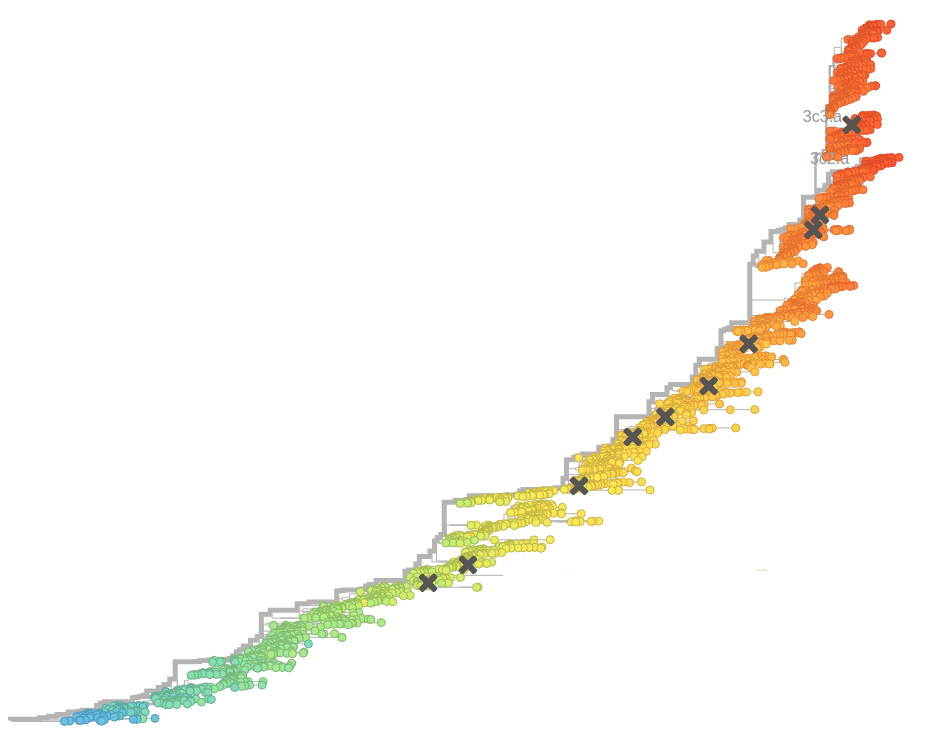
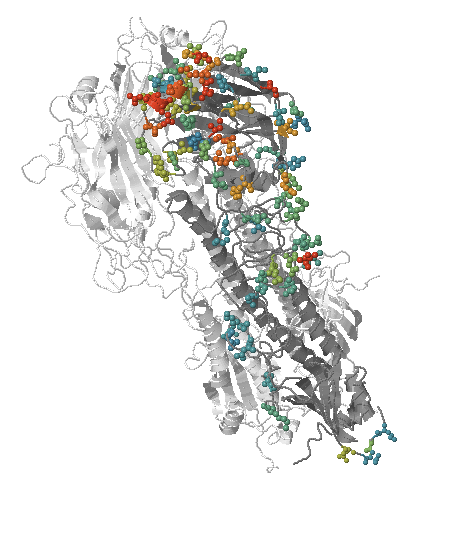
  • Influenza virus evolves to avoid human immunity
  • Vaccines need frequent updates

Kingman coalescent

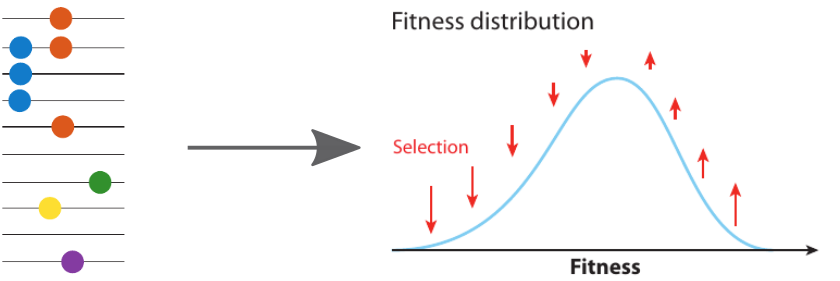
strong selection

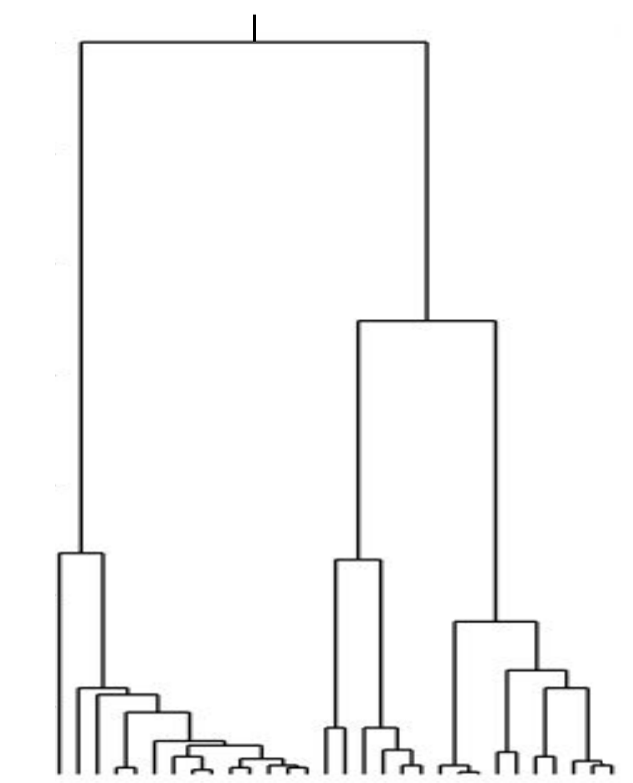
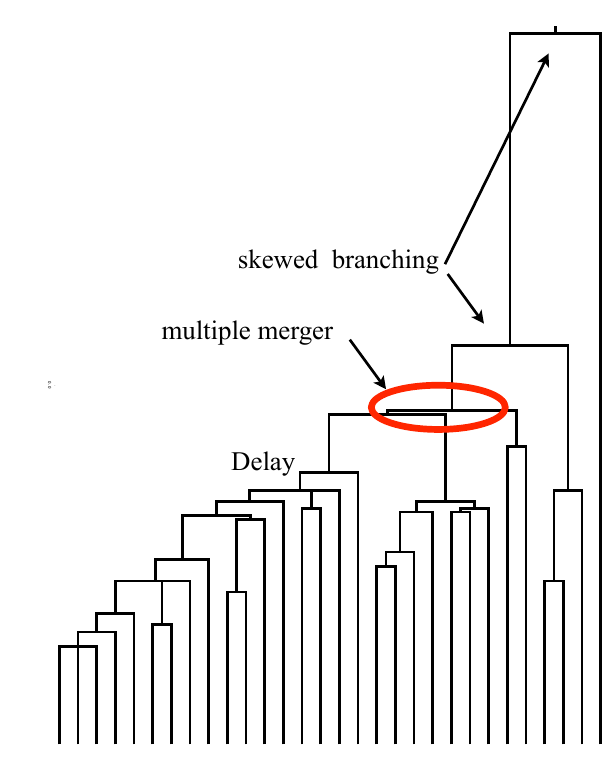
Bolthausen-Sznitman Coalescent

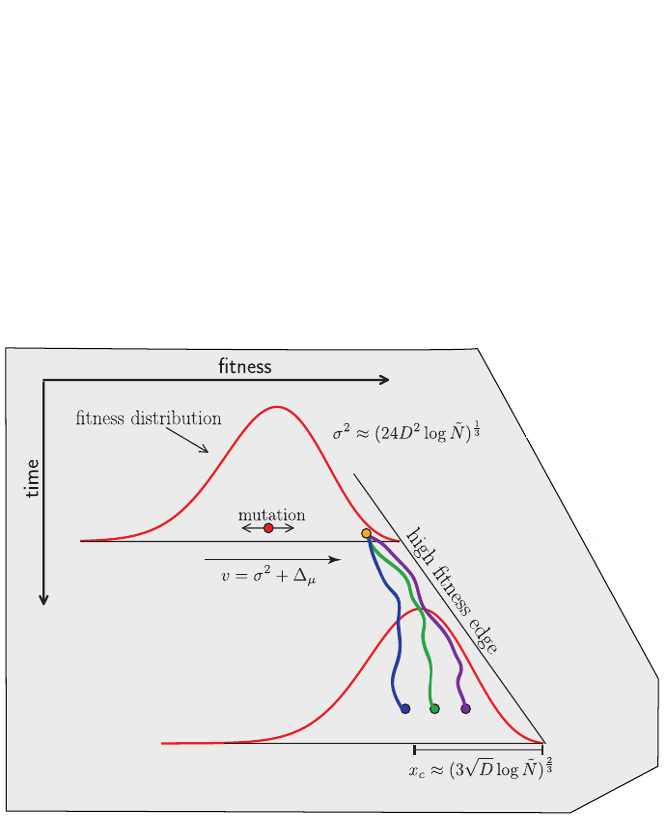
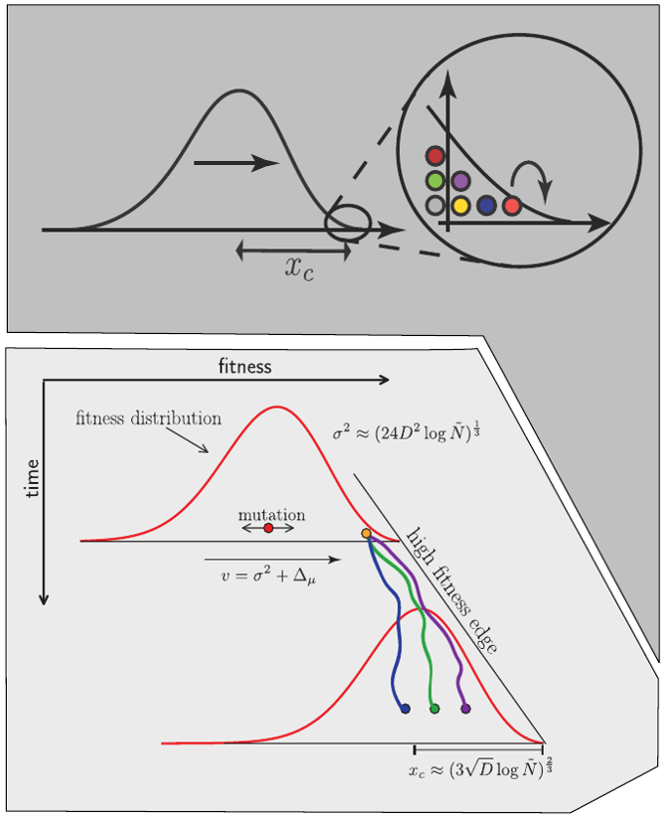
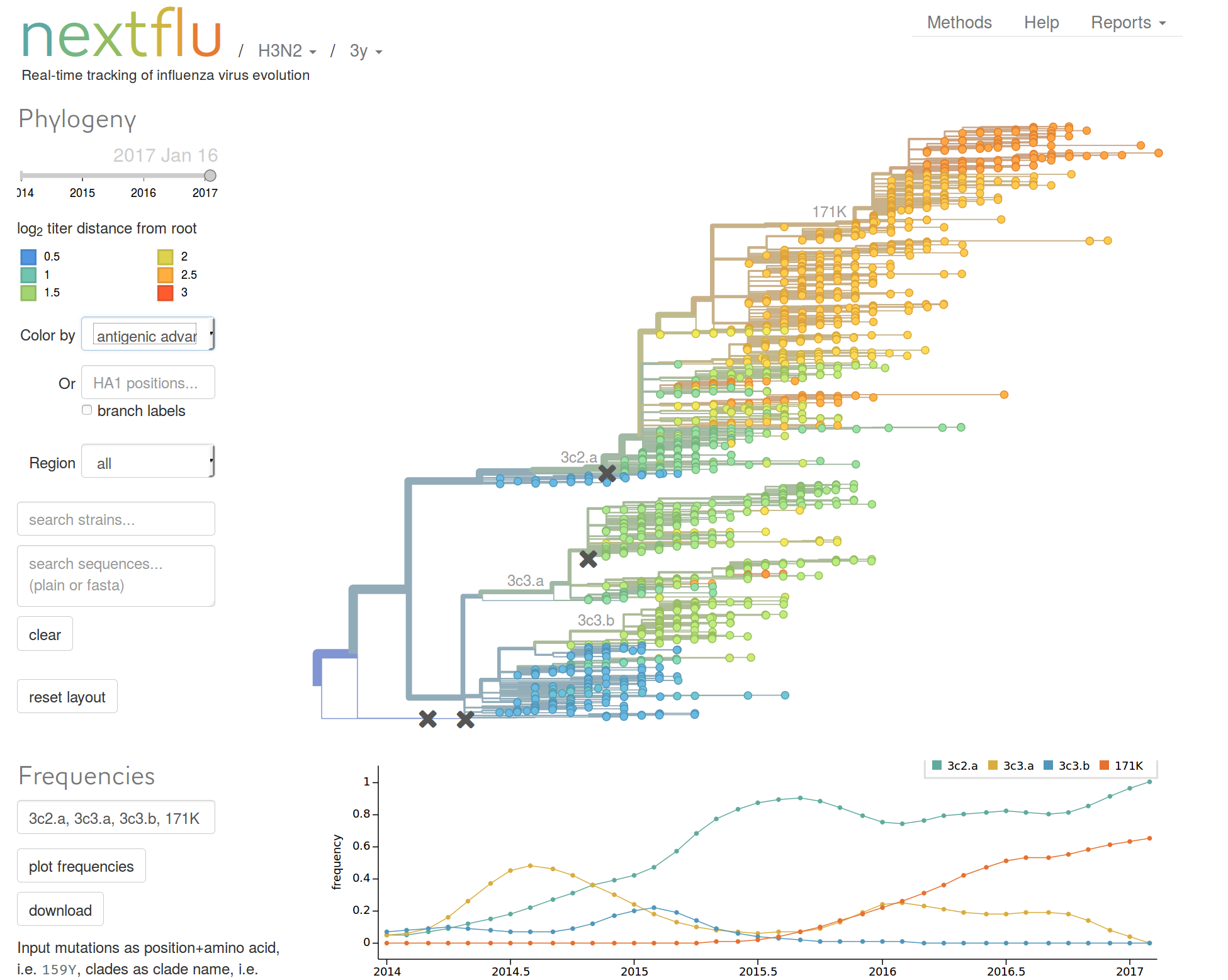
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007

Predicting evolution

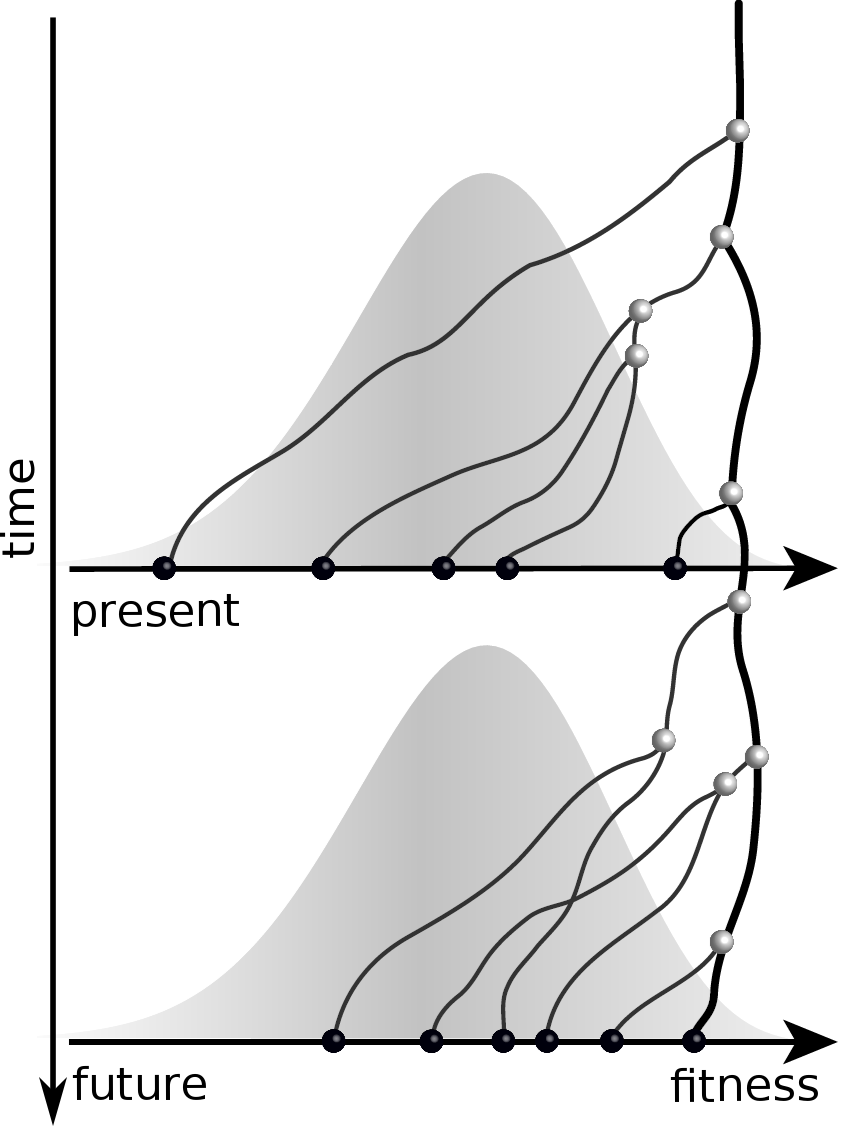
Given the branching pattern,
  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

RN, Russell, Shraiman, eLife, 2014
nextflu.org

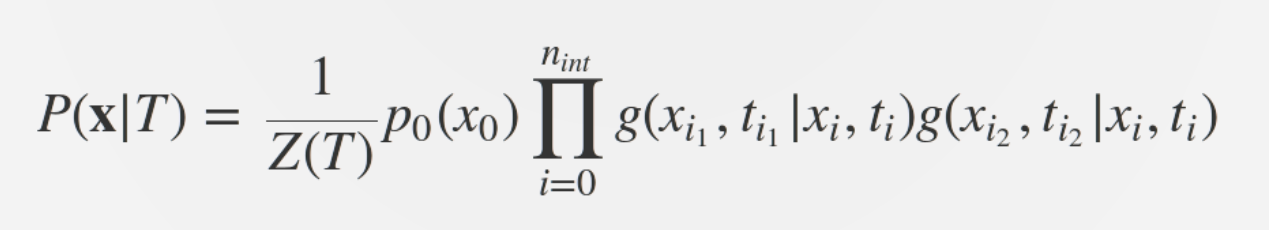
Prediction of the dominating H3N2 influenza strain

RN, Russell, Shraiman, eLife, 2014

nextstrain.org

HIV acknowledgments

  • Fabio Zanini
  • Jan Albert
  • Johanna Brodin
  • Christa Lanz
  • Göran Bratt
  • Lina Thebo
  • Vadim Puller

Influenza and Theory acknowledgments

  • Boris Shraiman
  • Colin Russell
  • Trevor Bedford

nextstrain.org

  • Trevor Bedford
  • Colin Megill
  • Pavel Sagulenko
  • Wei Ding
  • Sidney Bell
  • James Hadfield