Virus evolution and the predictability of next year's flu
Richard Neher
Biozentrum, University of Basel
slides at neherlab.org/201709_GCB.html
Viruses
 tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
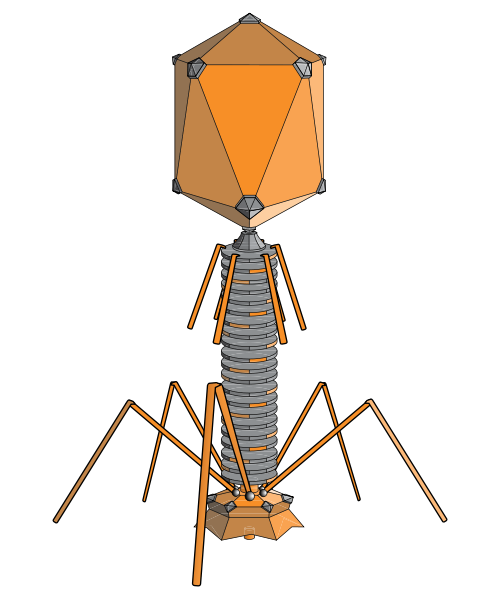
bacteria phage (adenosine, wikipedia)
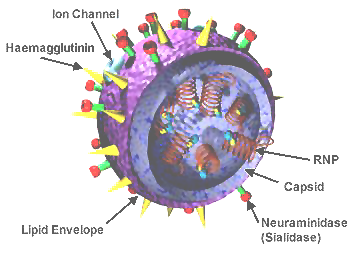
influenza virus wikipedia
human immunodeficiency virus wikipedia
- rely on host to replicate
- little more than genome + capsid
- genomes typically 5-200k bases (+exceptions)
- most abundant organisms on earth $\sim 10^{31}$
Evolution of HIV
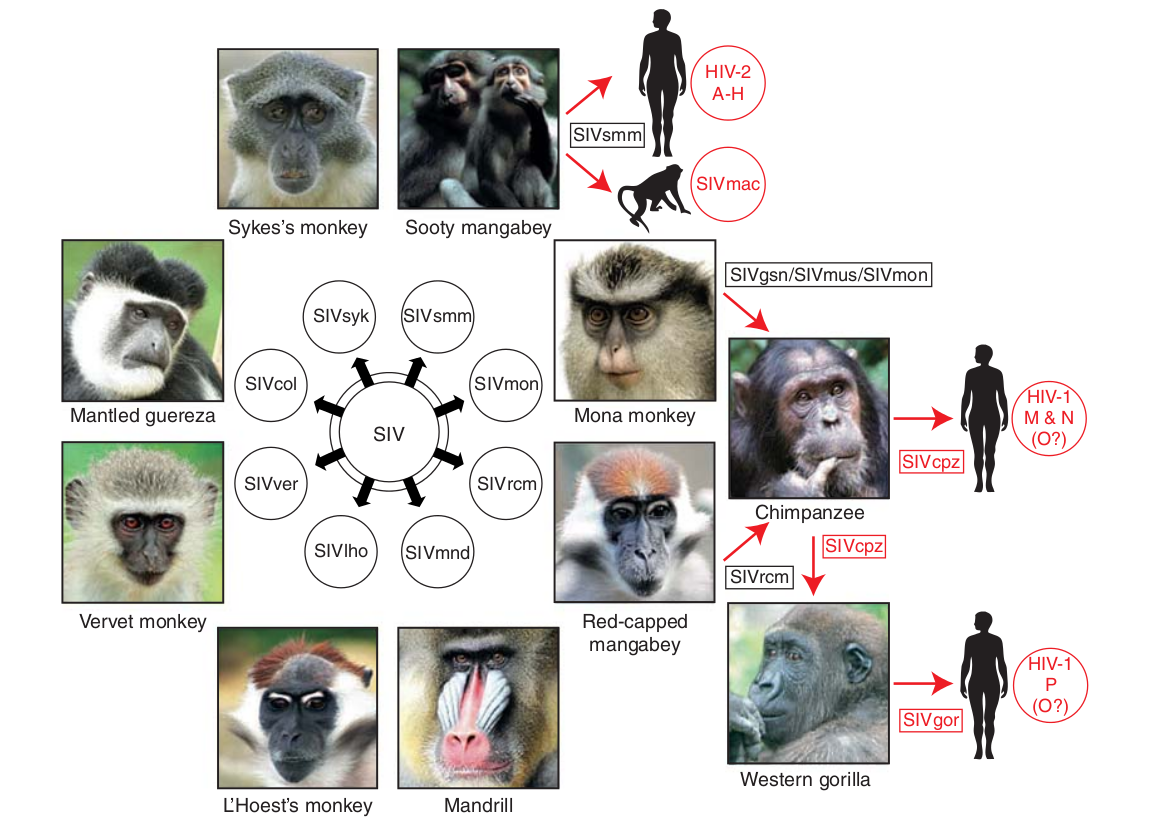
- Chimp → human transmission around 1900 gave rise to HIV-1 group M
- ~100 million infected people since
- subtypes differ at 10-20% of their genome
- HIV-1 evolves ~0.1% per year
HIV infection
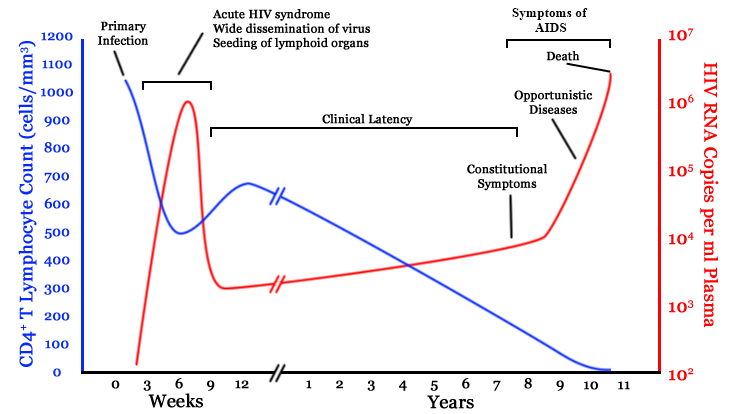
- $10^8$ cells are infected every day
- the virus repeatedly escapes immune recognition
- integrates into T-cells as
latent provirus
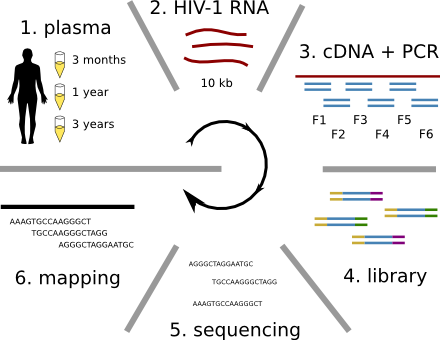
HIV-1 evolution within one individual

HIV acknowledgments







- Fabio Zanini
- Jan Albert
- Johanna Brodin
- Christa Lanz
- Göran Bratt
- Lina Thebo
- Vadim Puller



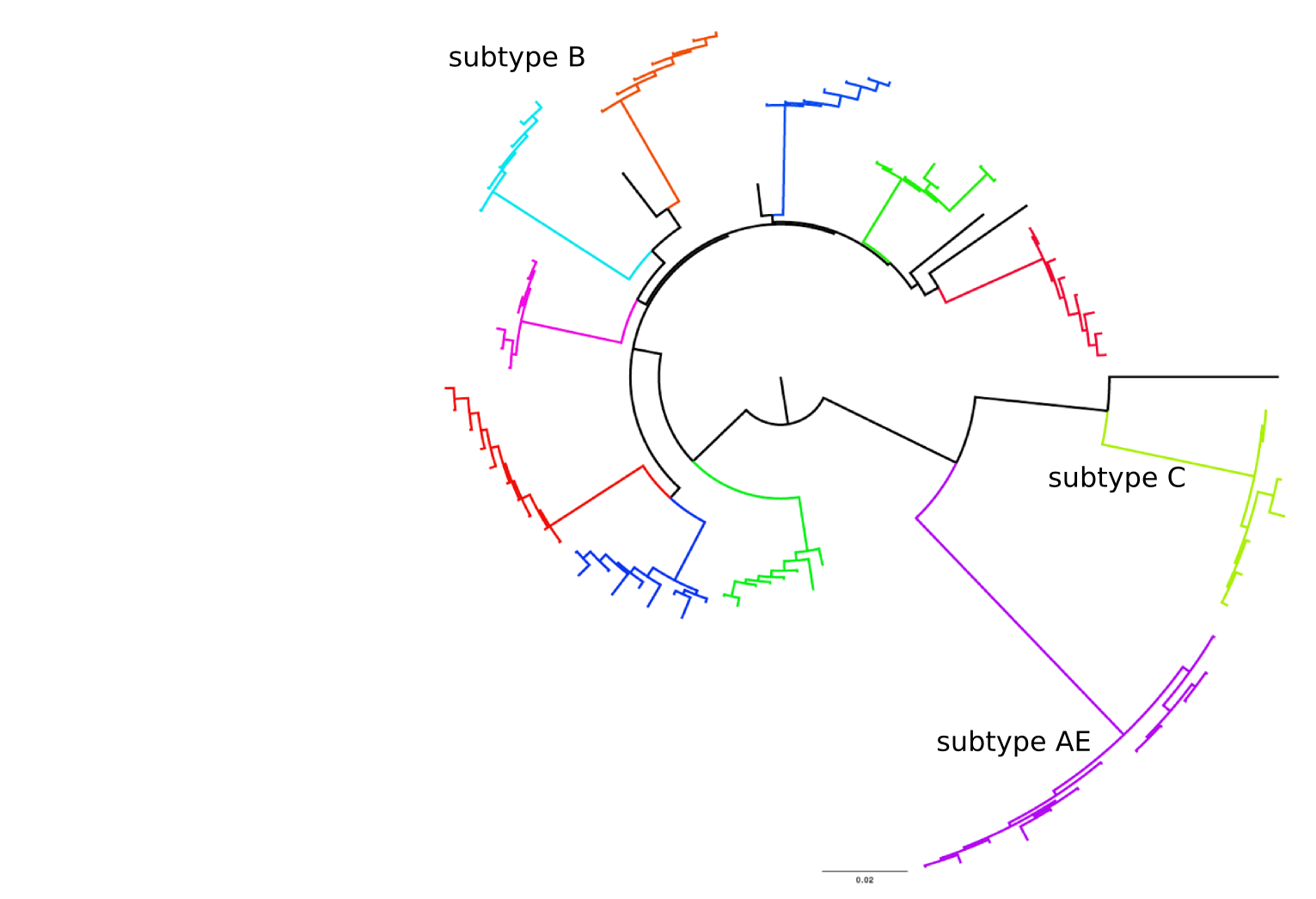
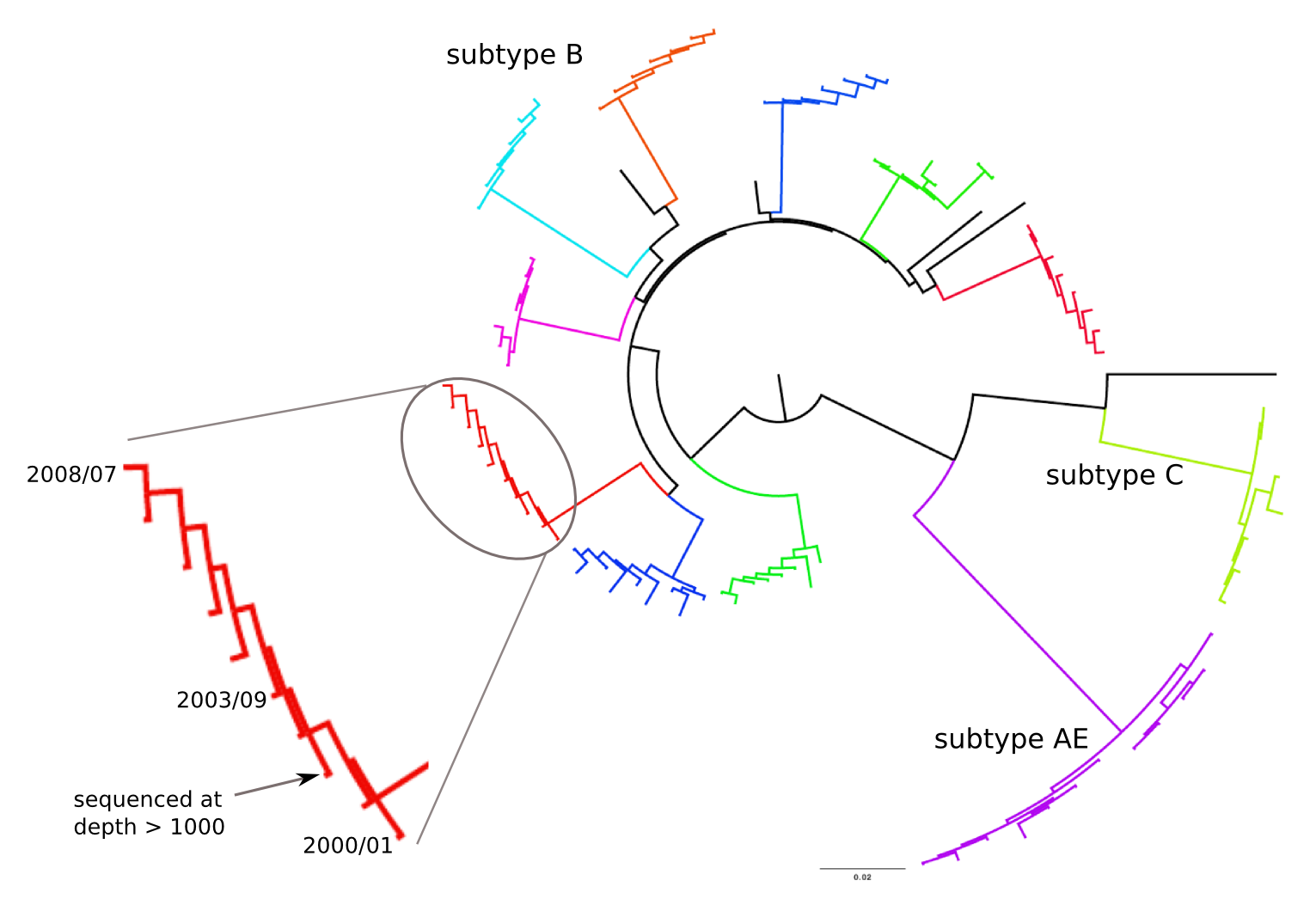
Population sequencing to track all mutations above 1%
- diverge at 0.1-1% per year
- almost whole genome coverage in 10 patients
- full data set at hiv.tuebingen.mpg.de
Diversity and hitchhiking
- envelope changes fastest, enzymes lowest
- identical rate of synonymous evolution
- diversity saturates where evolution is fast
- synonymous mutations stay at low frequency
Mutation rates and diversity at neutral sites
Inference of fitness costs
- mutation away from preferred state at rate $\mu$
- selection against non-preferred state with strength $s$
- variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
- equilibrium frequency: $\bar{x} = \mu/s $
- fitness cost: $s = \mu/\bar{x}$
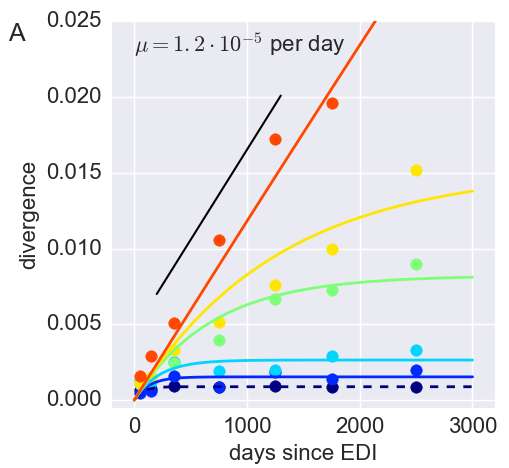
Inference of fitness costs
- Frequencies of costly mutations decorrelate fast $\frac{d x}{dt} = \mu -s x $
- $\Rightarrow$ average many samples to obtain accurate estimates
- Assumption: The global consensus is the preferred state
- Only use sites that initially agree with consensus
- Only use sites that don't chance majority nucleotide
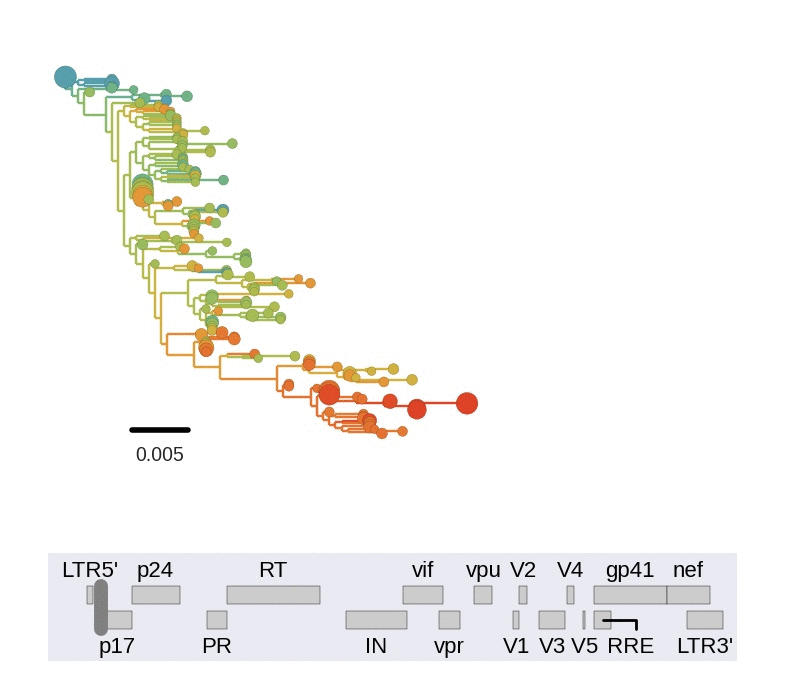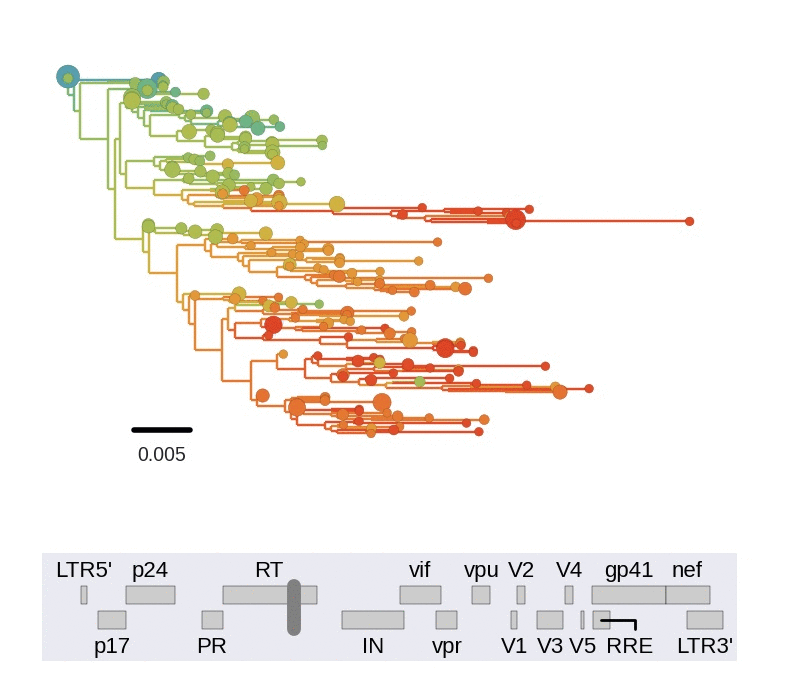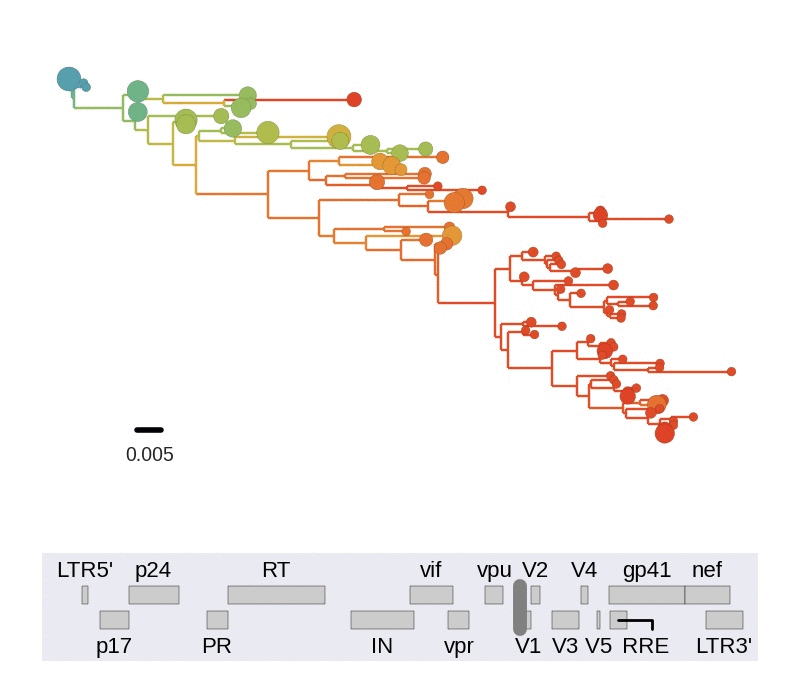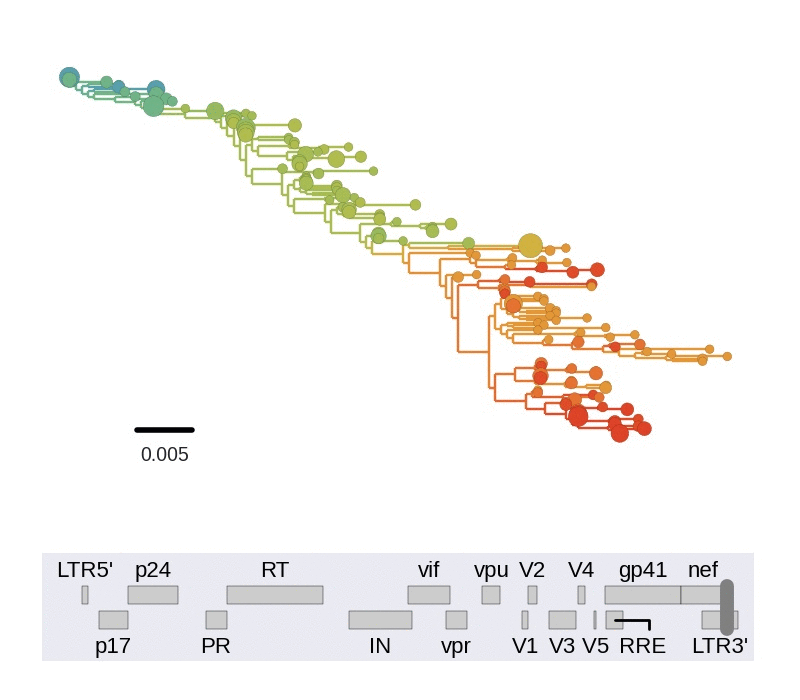
Fitness landscape of HIV-1
Zanini et al, Virus Evolution, 2017Selection on RNA structures and regulatory sites
Zanini et al, Virus Evolution, 2017Does HIV evolve during therapy?
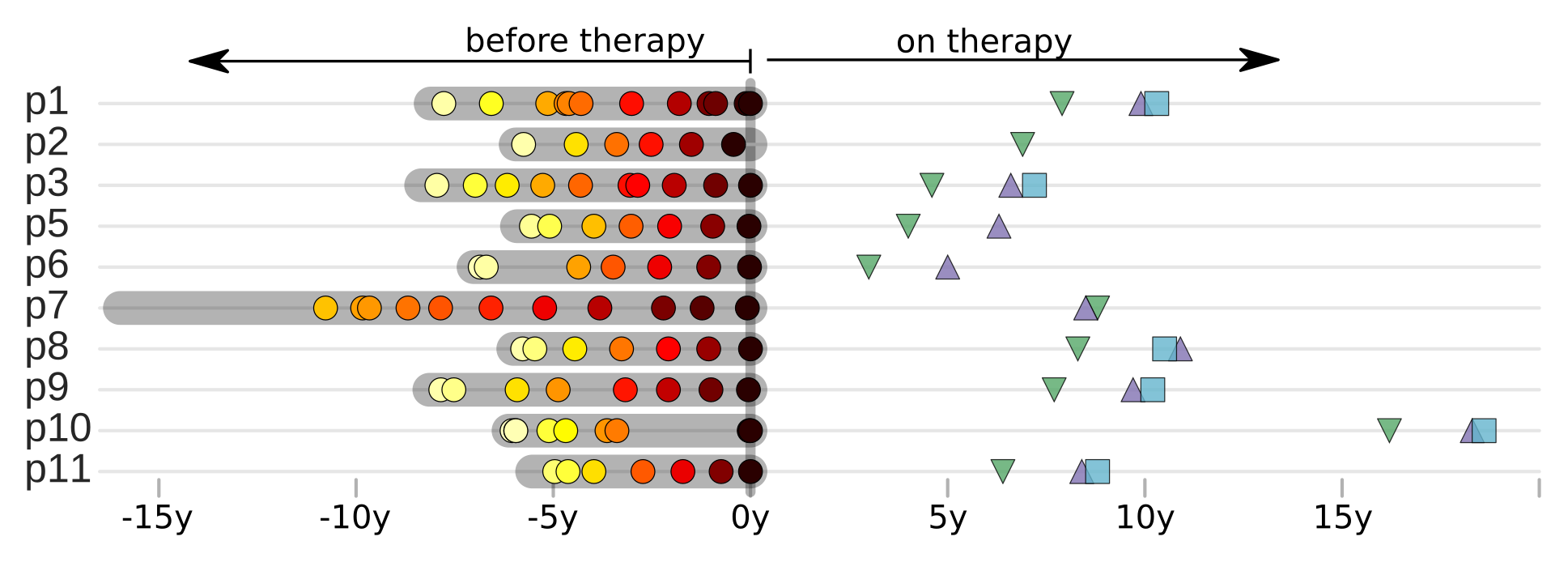 Brodin et al, eLife, 2016
Brodin et al, eLife, 2016
No evidence of ongoing replication
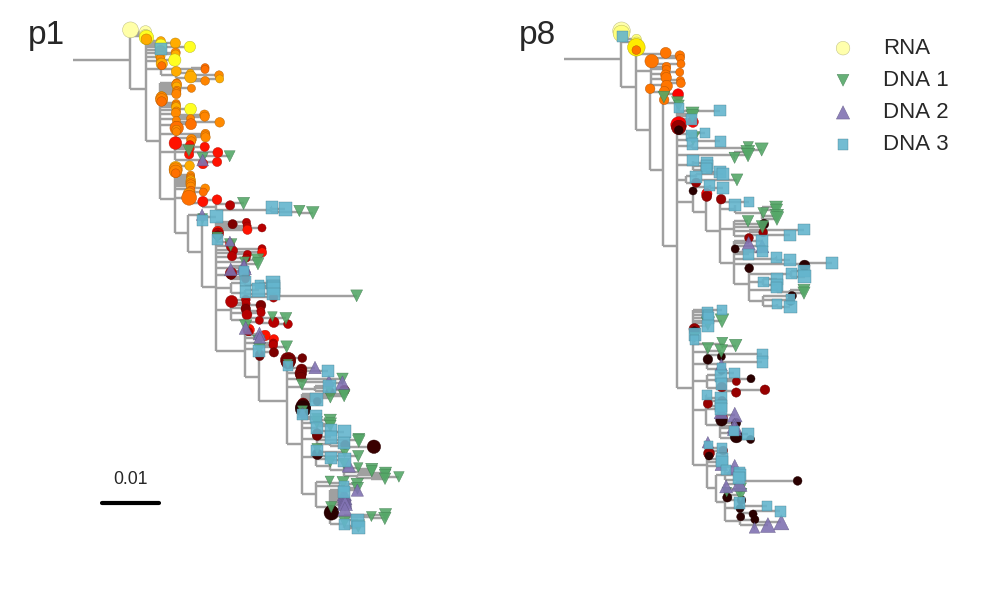
No evidence of ongoing replication
Theoretical framework for virus evolution -- population genetics
evolutionary processes ↔ trees ↔ genetic diversity
Neutral models and beyond
Neutral models
- all individuals are identical → same offspring distribution
- Kingman coalesence and diffusion theory are dual descriptions
- everything is easy to calculate
- perturbations like background selection can be included
But: neutral models not suitable for RNA viruses!
Influenza and Theory acknowledgments




- Boris Shraiman
- Colin Russell
- Trevor Bedford
- Oskar Hallatschek



Clonal interference and traveling waves
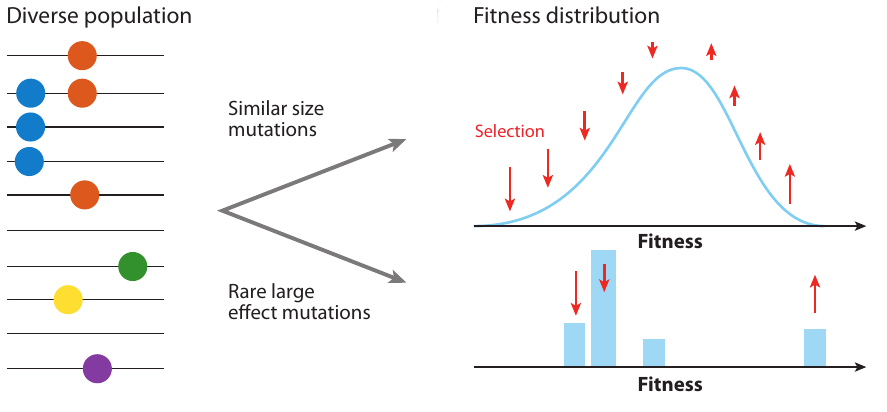
Neutral/Kingman coalescent
strong selection
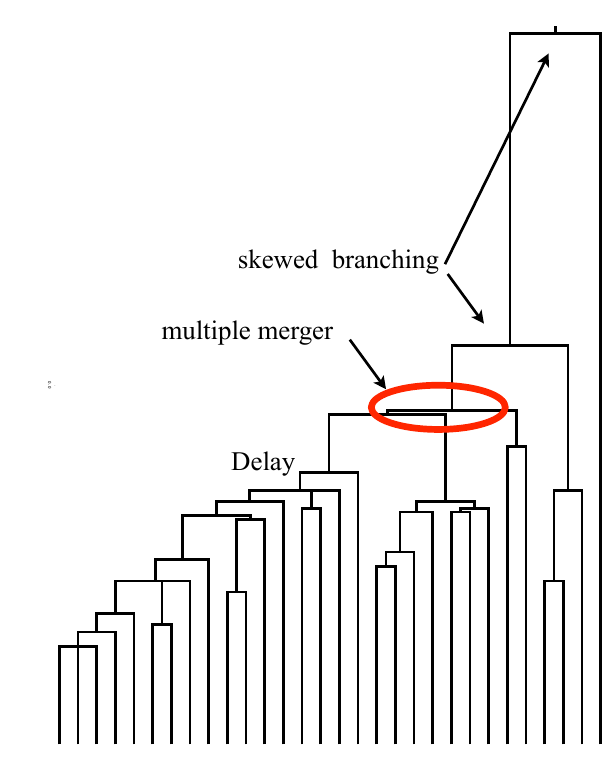
Bolthausen-Sznitman Coalescent
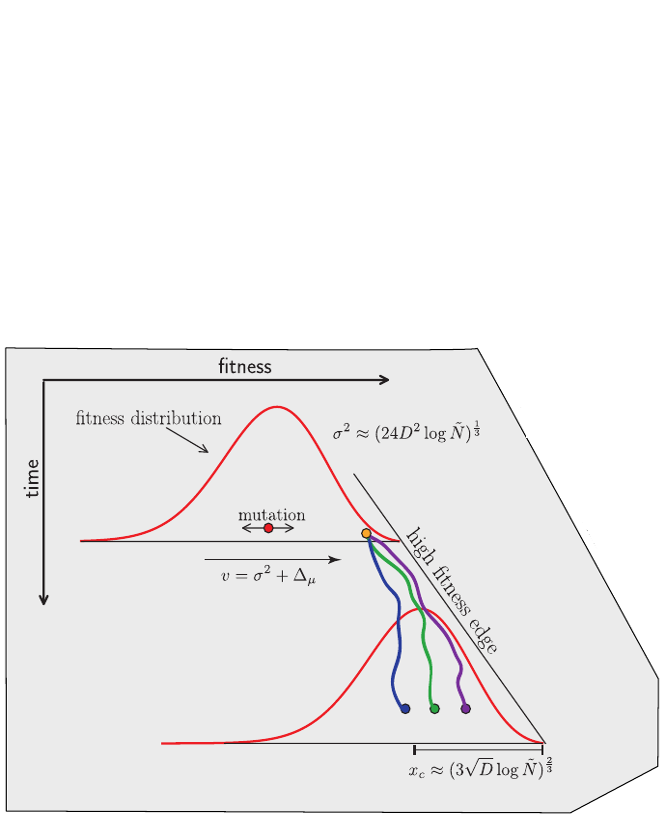
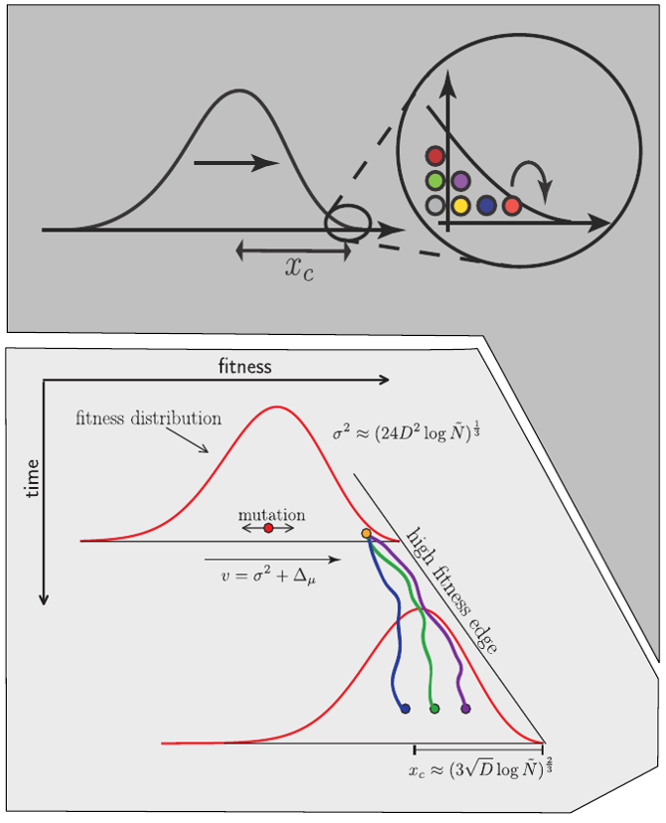
Bursts in a tree ↔ high fitness genotypes
Can we read fitness of a tree?
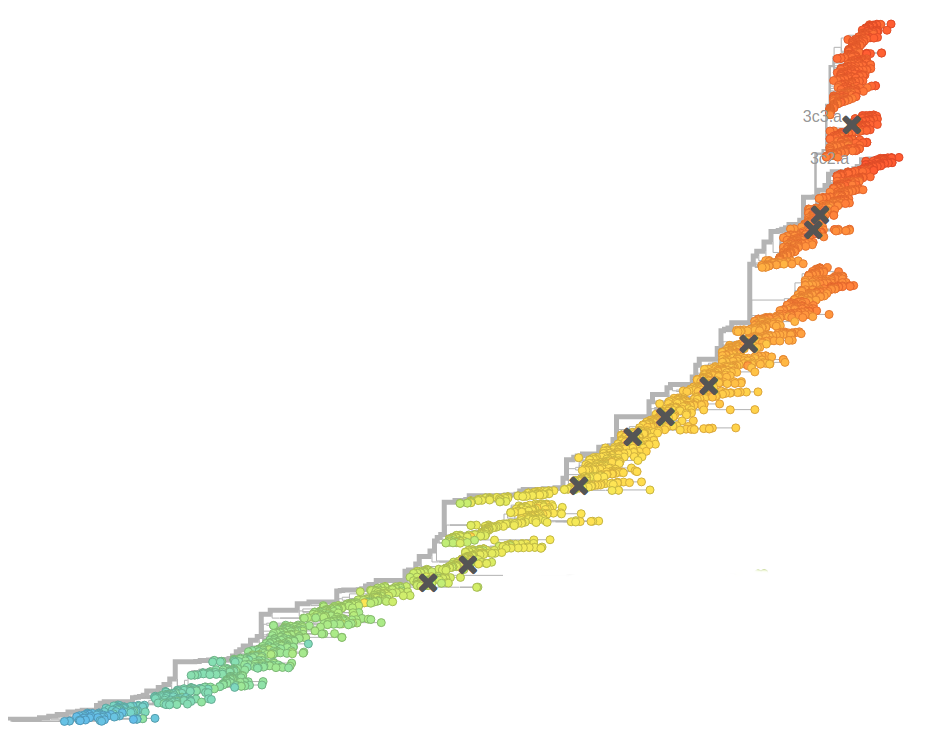
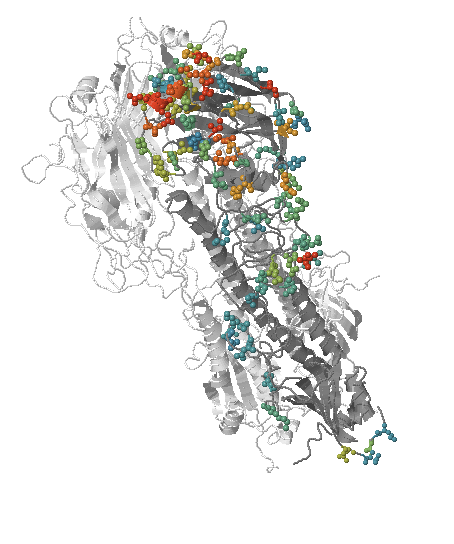
- Influenza virus evolves to avoid human immunity
- Vaccines need frequent updates
Predicting evolution
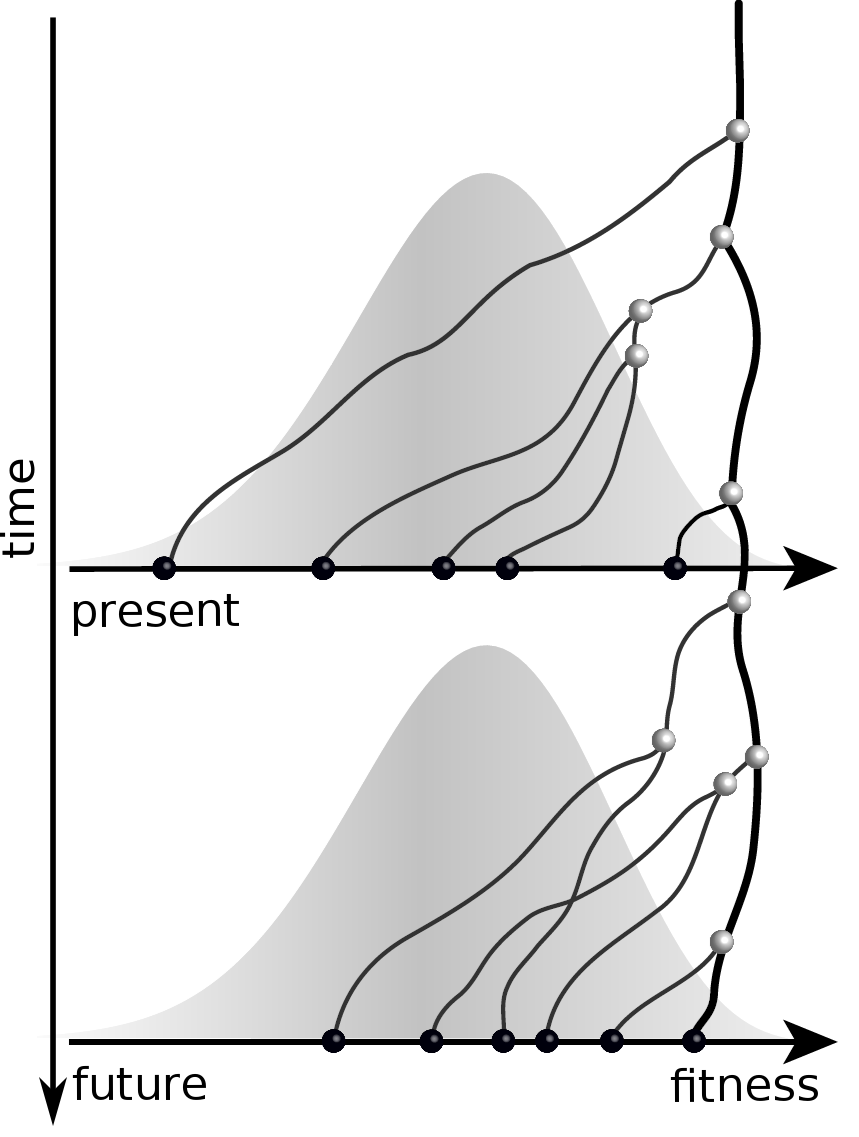
Given the branching pattern:
- can we predict fitness?
- pick the closest relative of the future?
Fitness inference from trees
$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014
Validate on simulation data
- simulate evolution
- sample sequences
- reconstruct trees
- infer fitness
- predict ancestor of future
- compare to truth

Validation on simulated data
Prediction of the dominating H3N2 influenza strain
- no influenza specific input
- how can the model be improved? (see model by Luksza & Laessig)
- what other context might this apply?
nextstrain.org
nextstrain.org






- Trevor Bedford
- Colin Megill
- Pavel Sagulenko
- Sidney Bell
- James Hadfield
- Wei Ding




Summary
- RNA virus evolution can be observed directly
- Rapidly adapting population require new population genetic models
- Those model can be used to infer fit clades
- Future influenza population can be anticipated
- Automated real-time analysis can help fight the spread of disease
HIV acknowledgments







- Fabio Zanini
- Jan Albert
- Johanna Brodin
- Christa Lanz
- Göran Bratt
- Lina Thebo
- Vadim Puller



Influenza and Theory acknowledgments




- Boris Shraiman
- Colin Russell
- Trevor Bedford
- Oskar Hallatschek


nextstrain.org






- Trevor Bedford
- Colin Megill
- Pavel Sagulenko
- Sidney Bell
- James Hadfield
- Wei Ding



