Virus evolution and the spread of infectious disease


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/20171101_Ringvorlesung.html

Viruses

tobacco mosaic virus (Thomas Splettstoesser, wikipedia)

bacteria phage (adenosine, wikipedia)

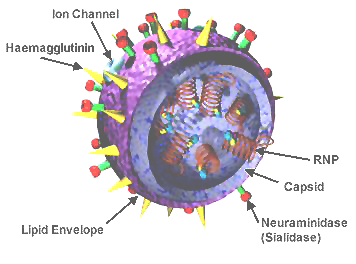
influenza virus wikipedia

human immunodeficiency virus wikipedia
  • rely on host to replicate
  • little more than genome + capsid
  • genomes typically 5-200k bases (+exceptions)
  • most abundant organisms on earth $\sim 10^{31}$

Lifecycle of animal viruses

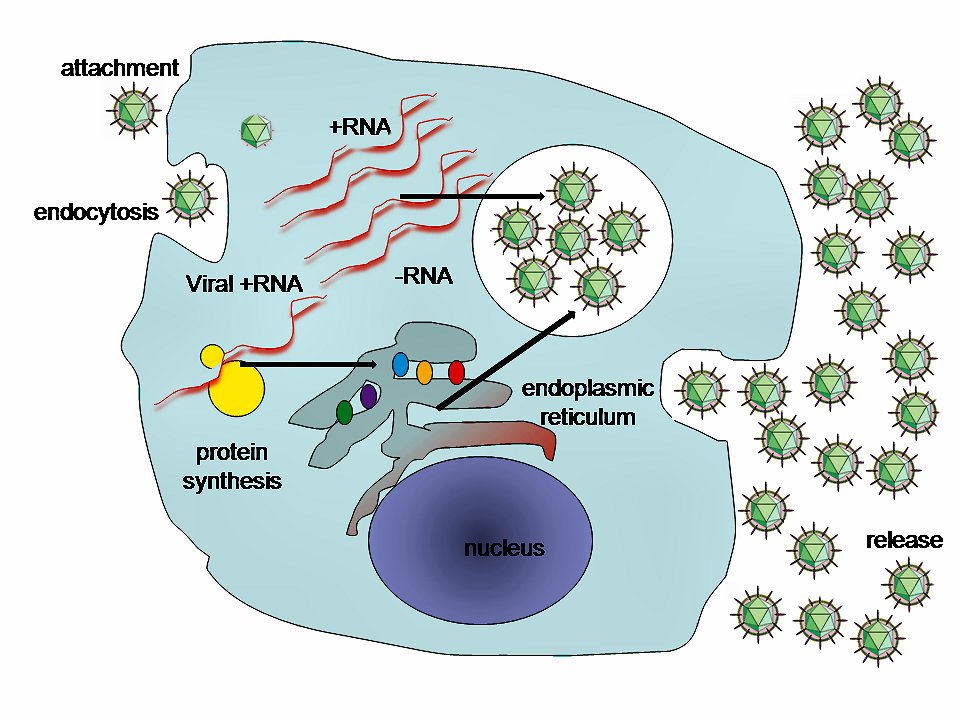By GrahamColm at English Wikipedia

Some viruses evolve a million times faster than animals

Animal haemoglobin

HIV protein

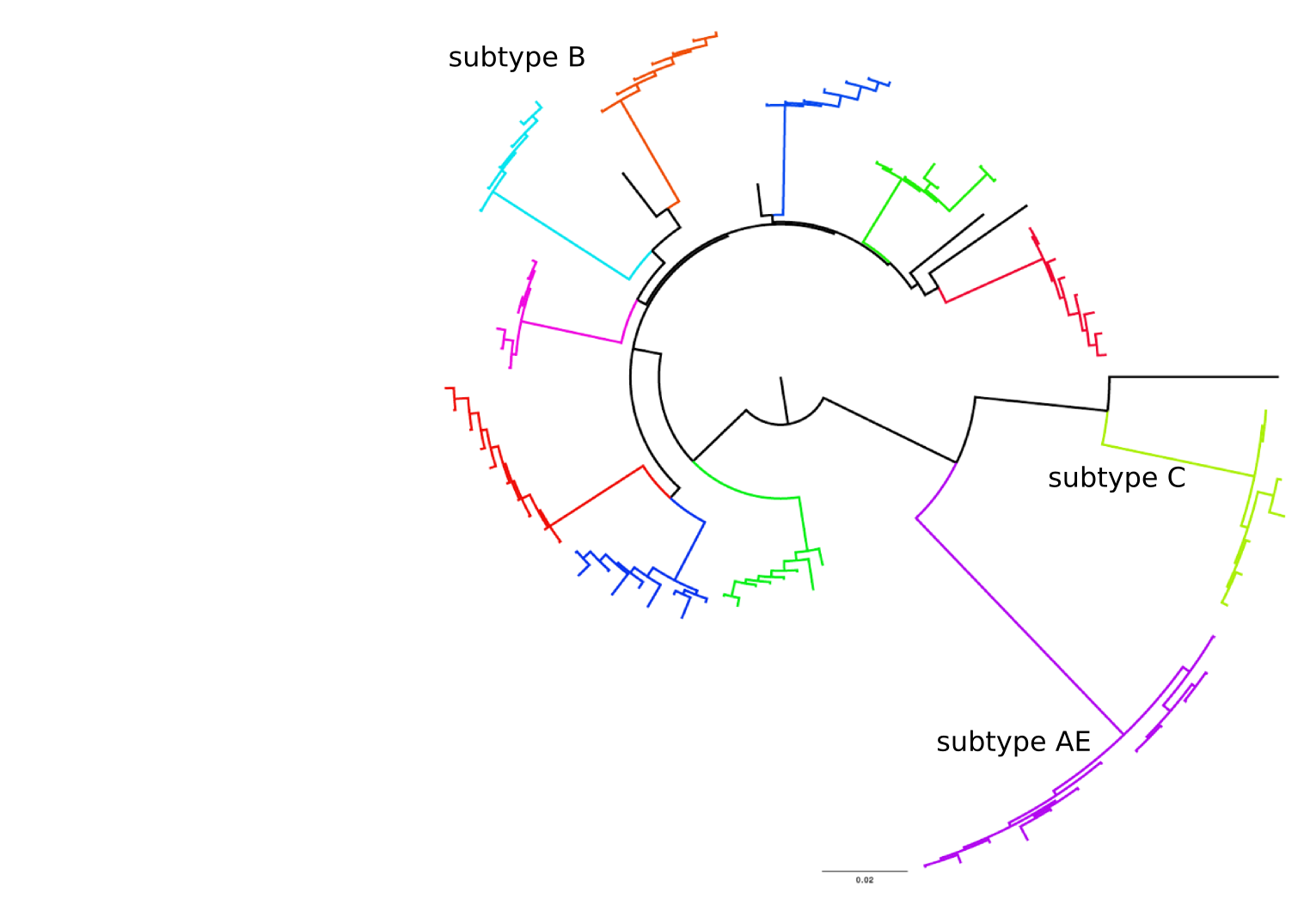
Evolution of HIV


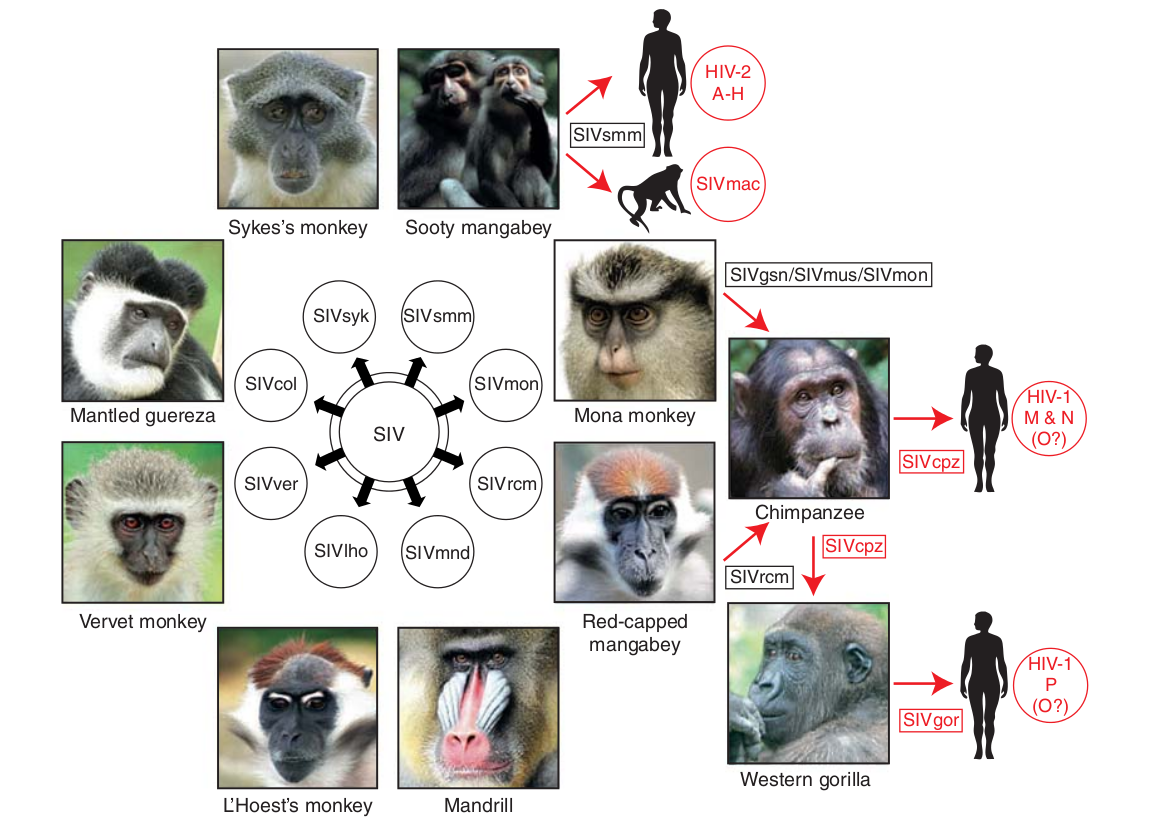
  • Chimp → human transmission around 1900 gave rise to HIV-1 group M
  • ~100 million infected people since
  • subtypes differ at 10-20% of their genome
  • HIV-1 evolves ~0.1% per year
image: Sharp and Hahn, CSH Persp. Med.

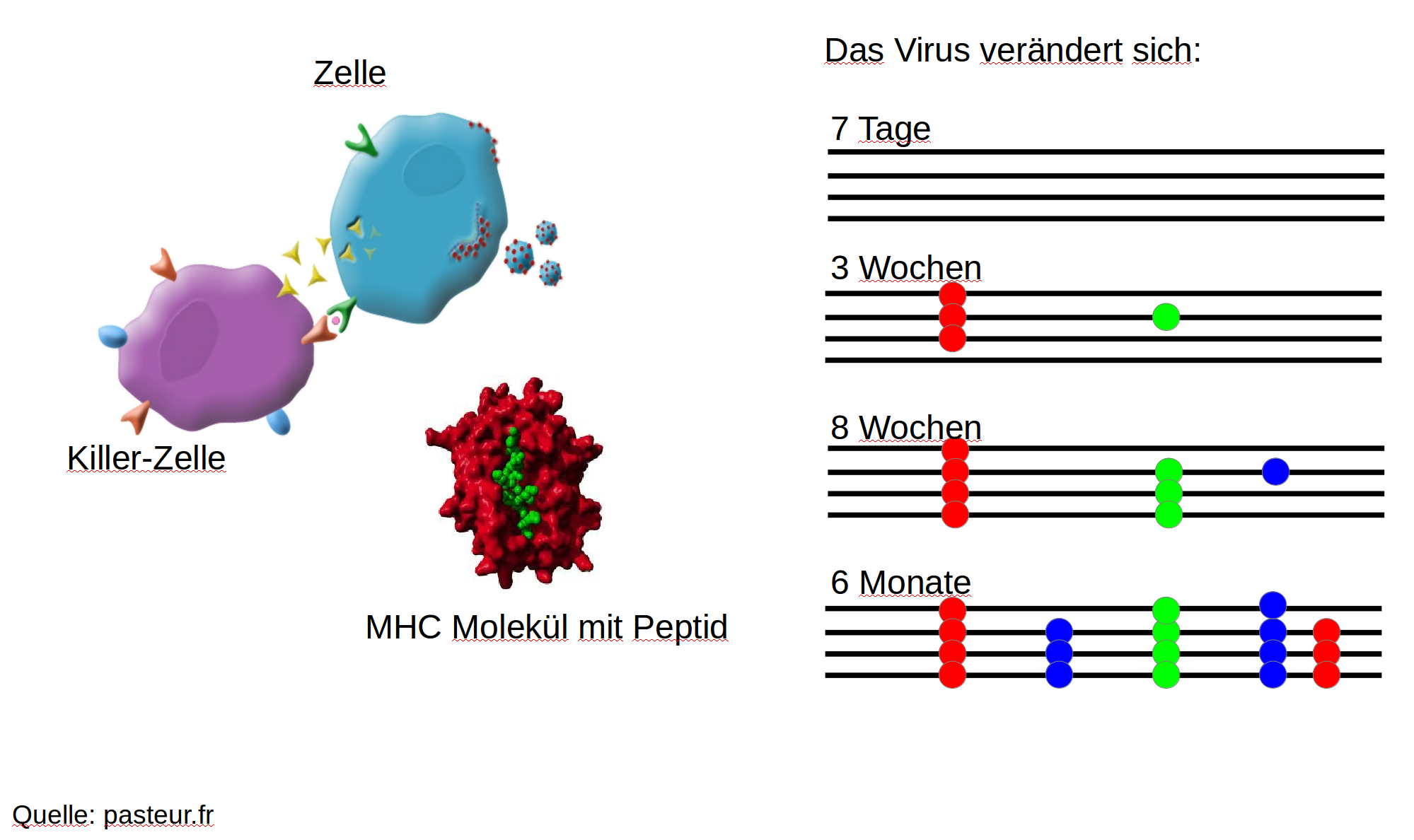
HIV infection

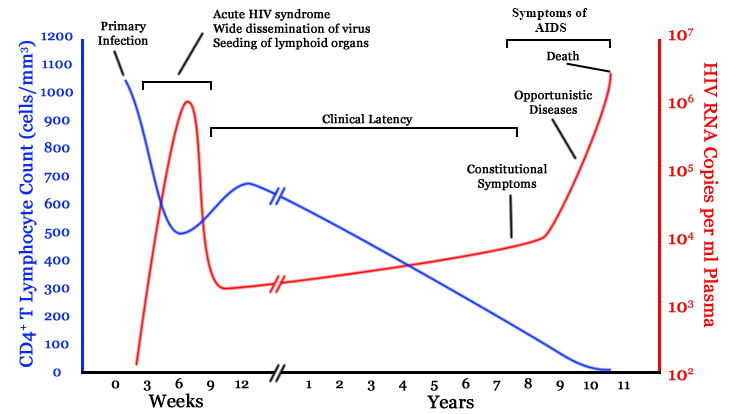
  • $10^8$ cells are infected every day
  • the virus repeatedly escapes immune recognition
  • integrates into T-cells as latent provirus
image: wikipedia

Development of sequencing technologies

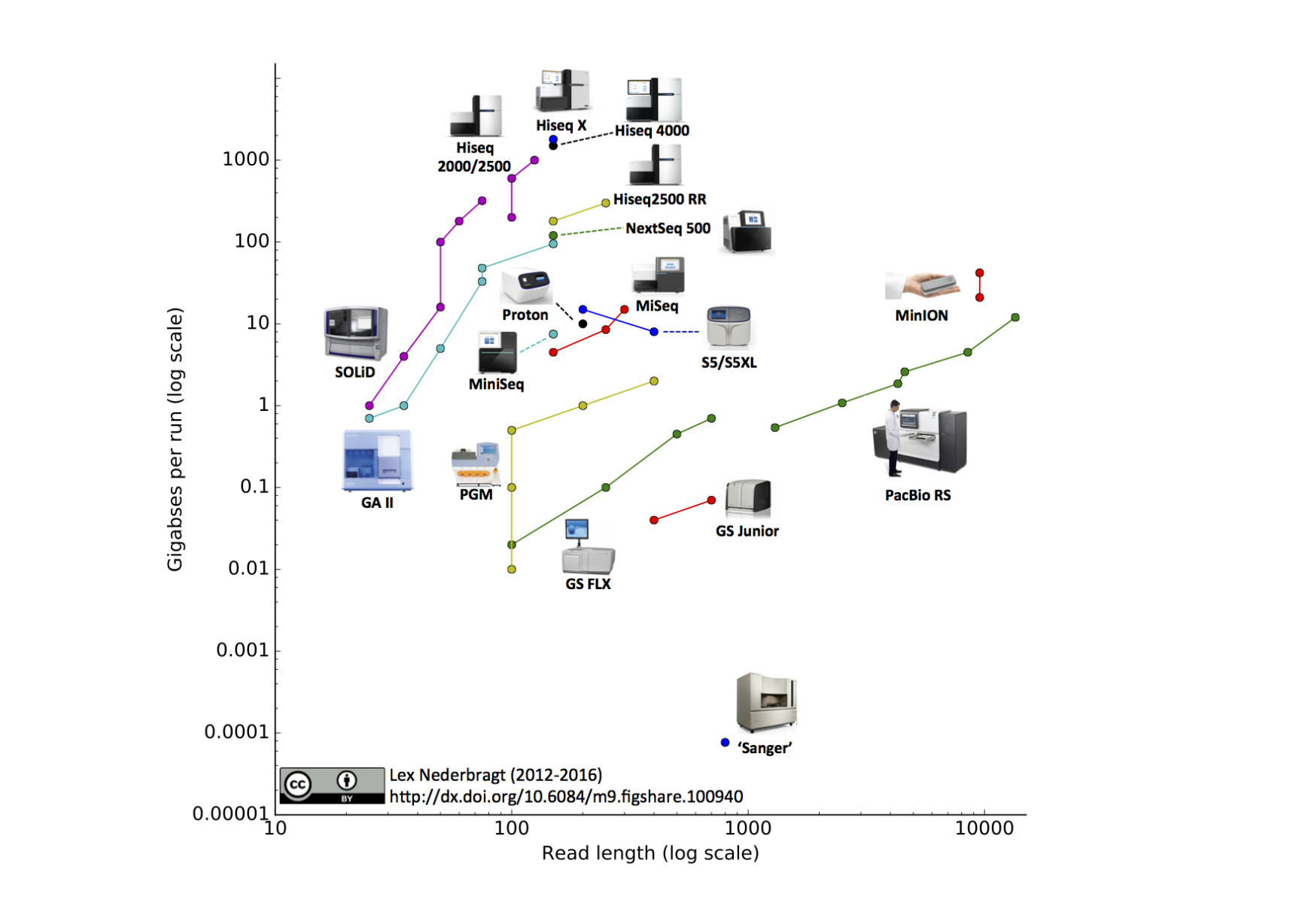
We can now sequence...
  • thousands of bacterial isolates
  • thousands of single cells
  • populations of viruses, bacteria or flies
  • diverse ecosystems

HIV-1 evolution within one individual



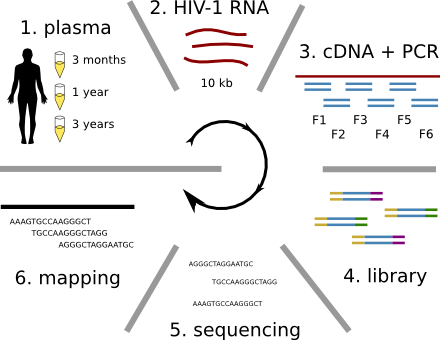
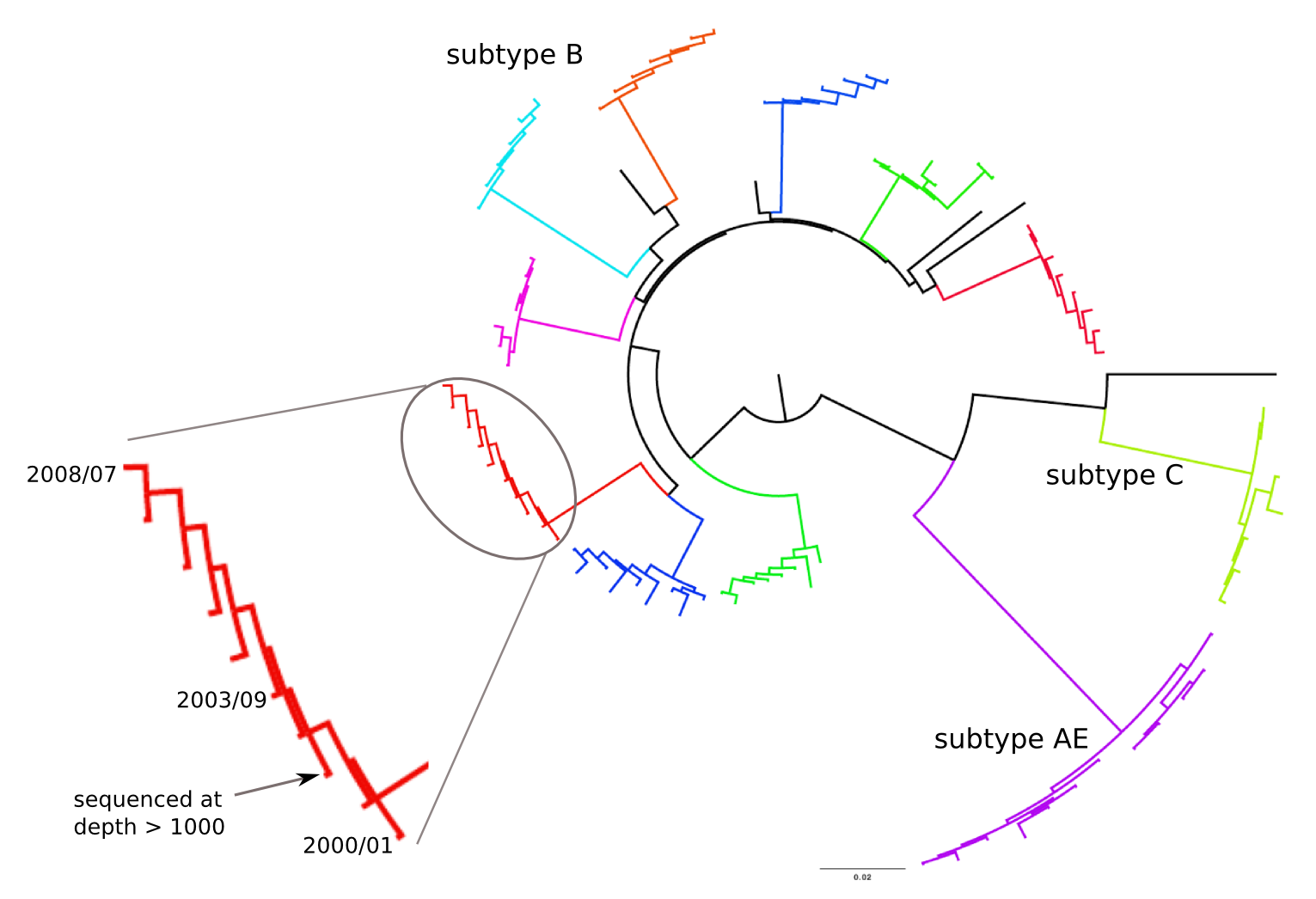
silouhette: clipartfest.com, Zanini at al, 2015. Collaboration with Jan Albert and his group


Immune escape in early HIV infection

Immune escape in early HIV infection

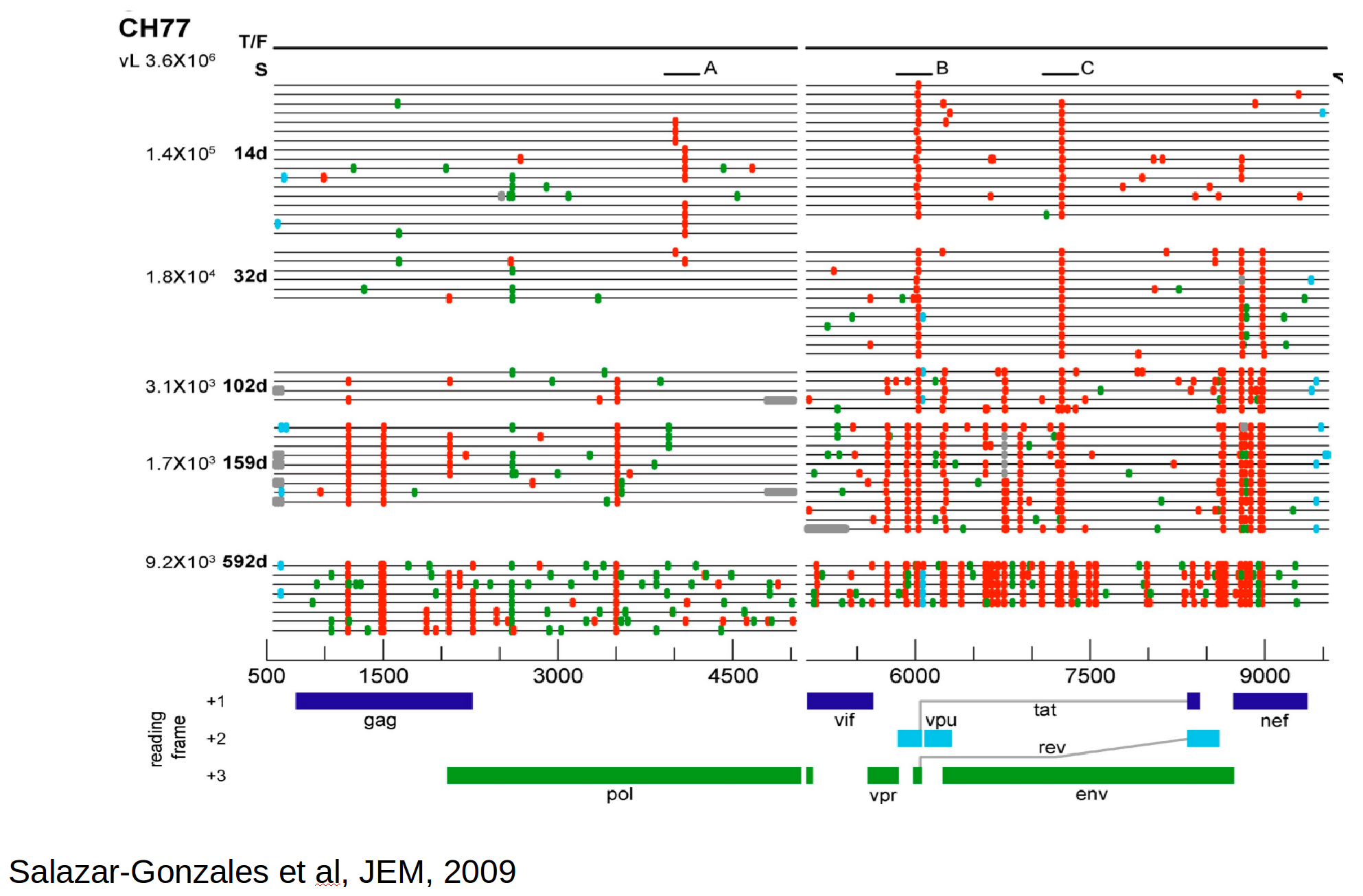
Population genetics & evolutionary dynamics

evolutionary processes ↔ trees ↔ genetic diversity

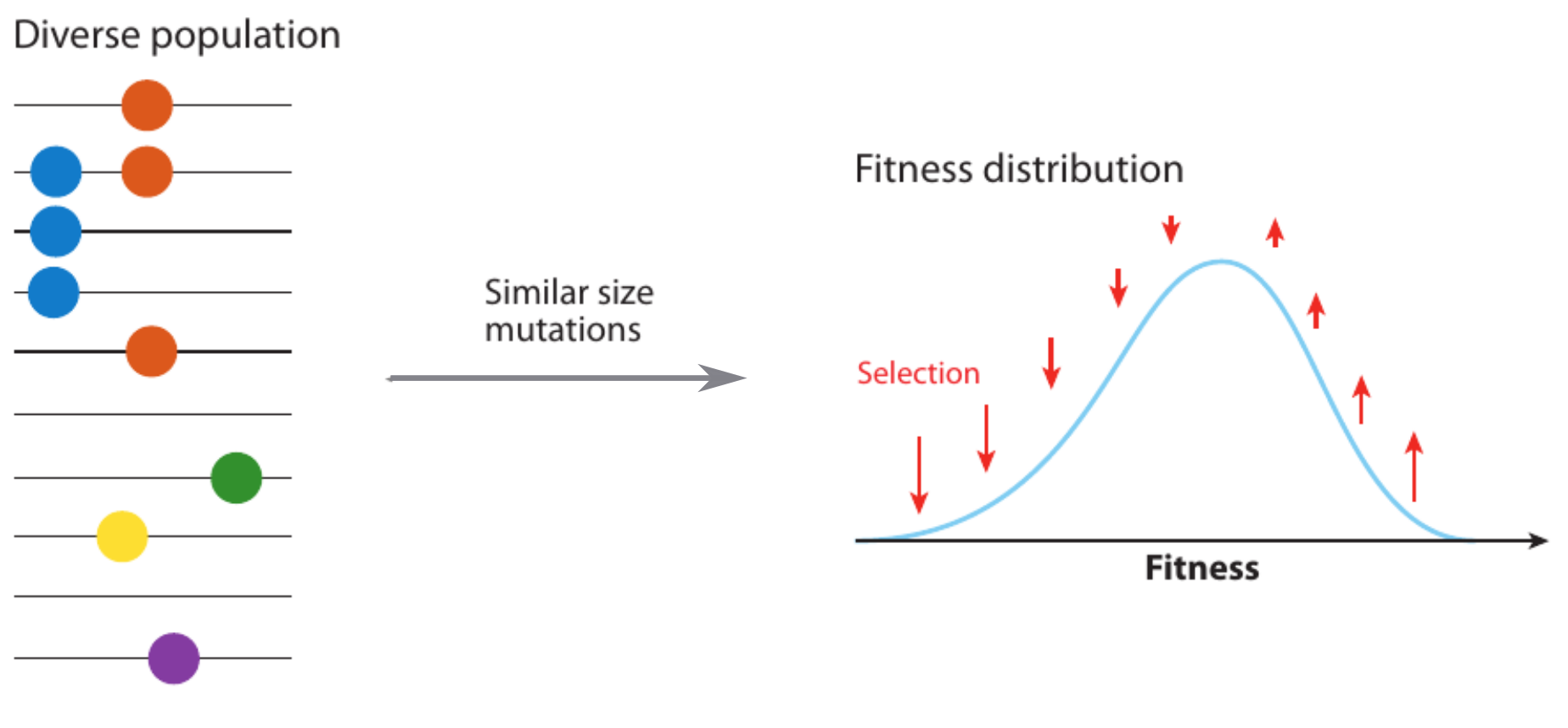
Selective sweeps

  • Viruses carrying a beneficial mutation have more offspring: on average $1+s$ instead of $1$
  • $s$ is called selection coefficient
  • Fraction $x$ of viruses carrying the mutation changes as $$x(t+1) = \frac{(1+s)x(t)}{(1+s)x(t) + (1-x(t))}$$
  • In continuous time → logistic differential equation: $$\frac{dx}{dt} = sx(1-x) \Rightarrow x(t) = \frac{e^{s(t-t_0)}}{1+ e^{s(t-t_0)}}$$

Population sequencing to track all mutations above 1%

  • diverge at 0.1-1% per year
  • almost whole genome coverage in 10 patients
  • full data set at hiv.tuebingen.mpg.de
Zanini et al, eLife, 2015; antibody data from Richman et al, 2003

The rate of sequence evolution in HIV

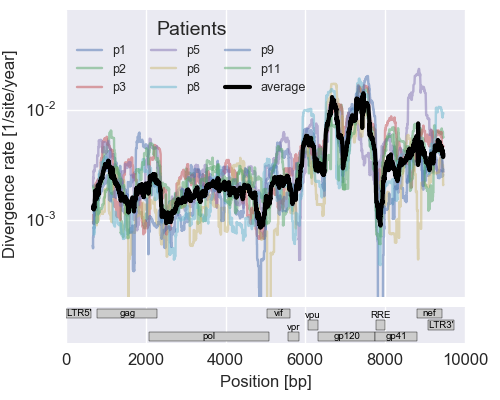
Evolution in different parts of the genome

  • envelope changes fastest, enzymes lowest
  • identical rate of synonymous evolution
  • diversity saturates where evolution is fast
  • synonymous mutations stay at low frequency
Zanini et al, eLife, 2015

Mutation rates and diversity and neutral sites

Zanini et al, Virus Evolution, 2017

Inference of fitness costs

  • mutation away from preferred state with rate $\mu$
  • selection against non-preferred state with strength $s$
  • variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
  • equilibrium frequency: $\bar{x} = \mu/s $
  • fitness cost: $s = \mu/\bar{x}$

Fitness landscape of HIV-1

Zanini et al, Virus Evolution, 2017

Selection on RNA structures and regulatory sites

Zanini et al, Virus Evolution, 2017

The distribution of fitness costs

Zanini et al, Virus Evolution, 2017

nextflu.org

joint work with Trevor Bedford & his lab

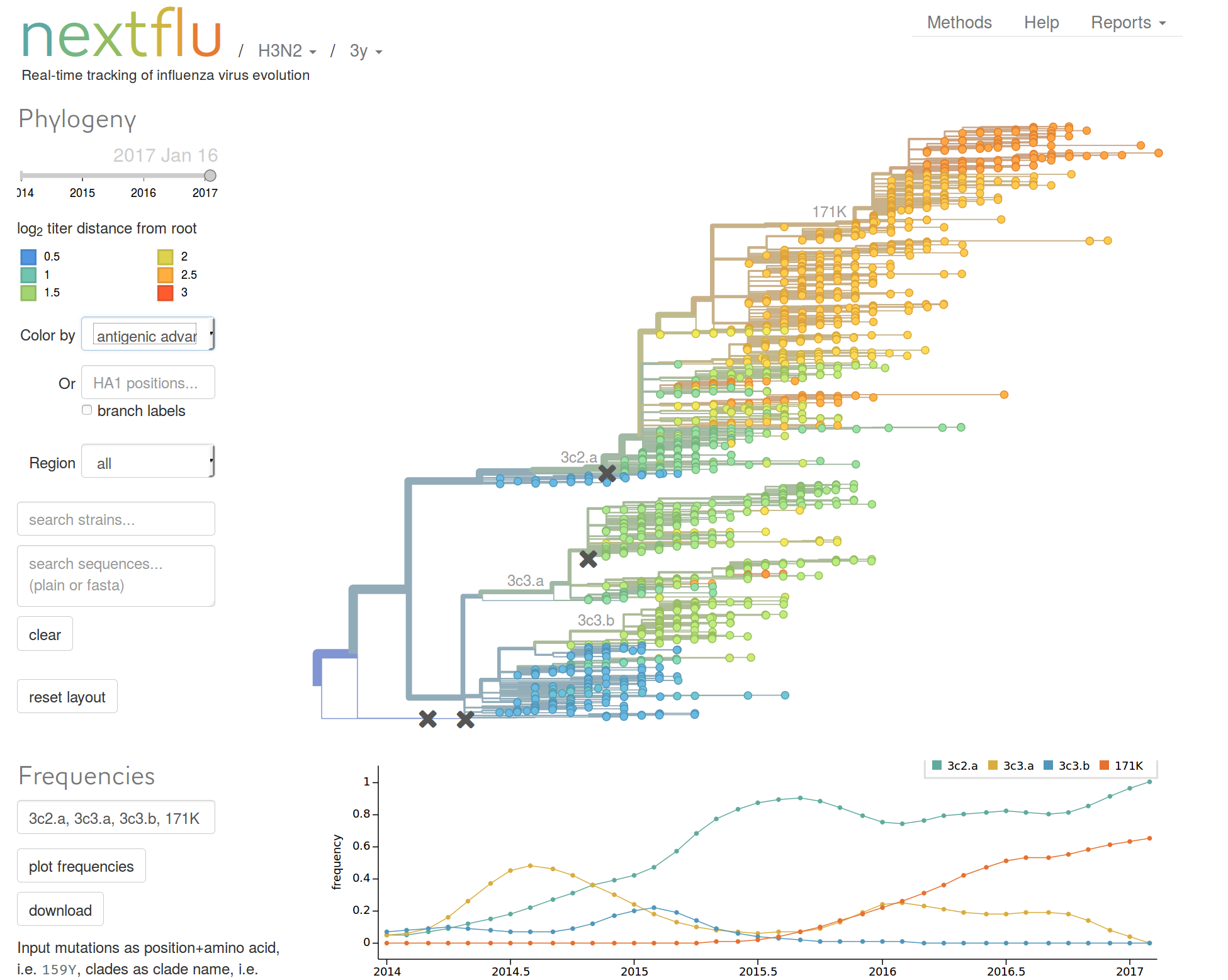
nextstrain.org

joint work with Trevor Bedford & his lab

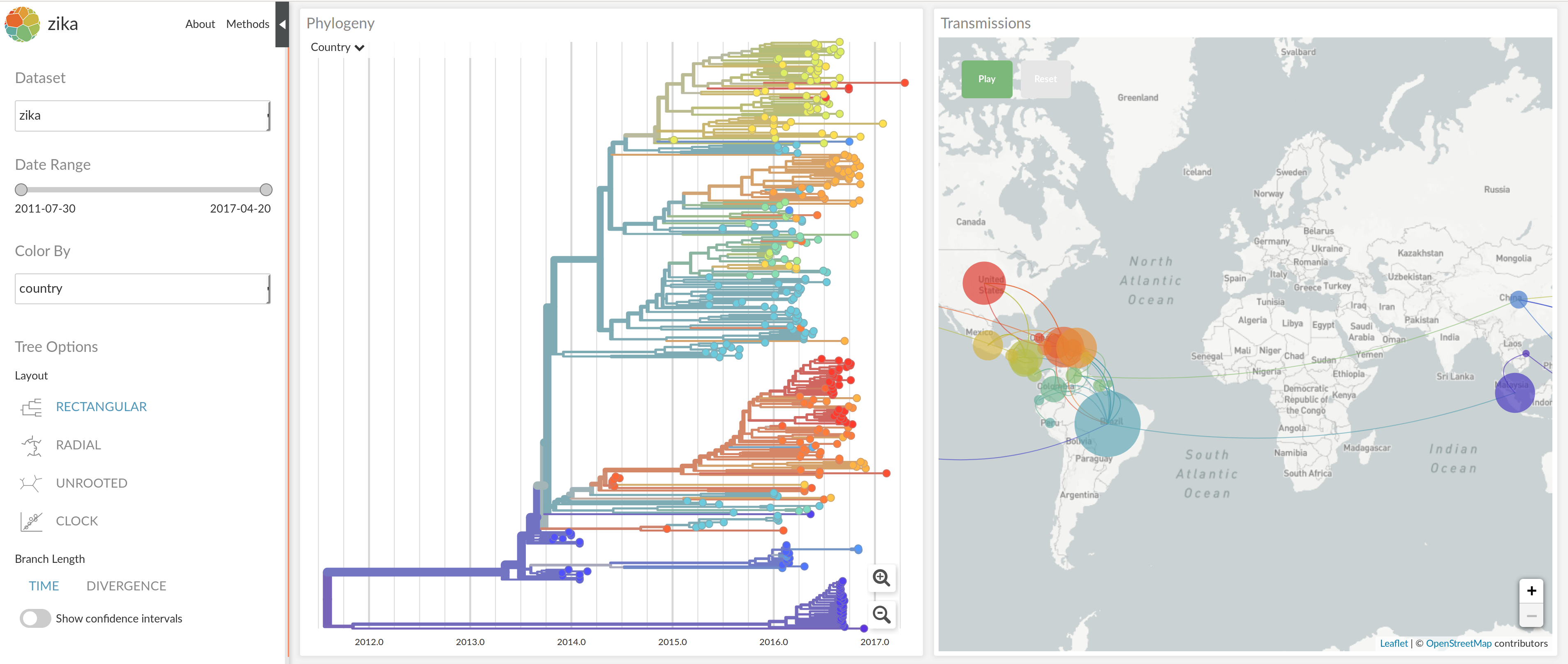
Clonal interference and traveling waves

RN, Annual Reviews, 2013; Desai & Fisher; Brunet & Derrida; Kessler & Levine

Typical tree

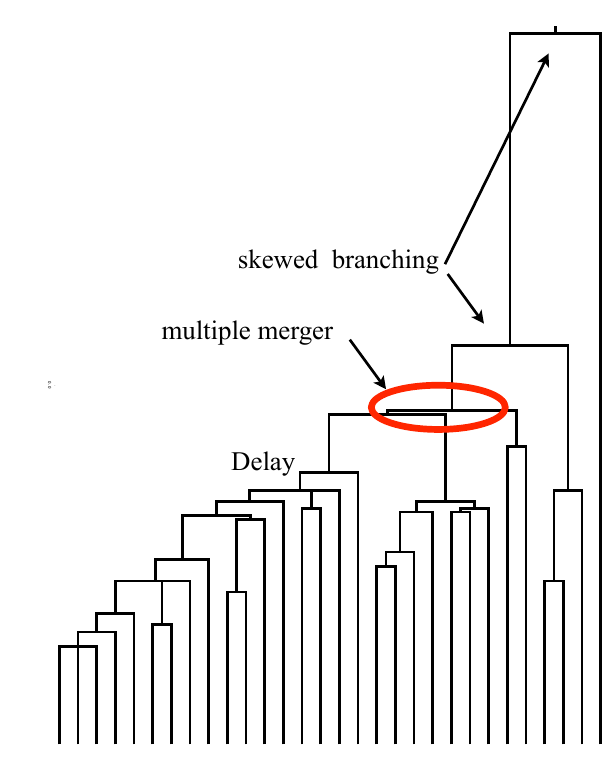
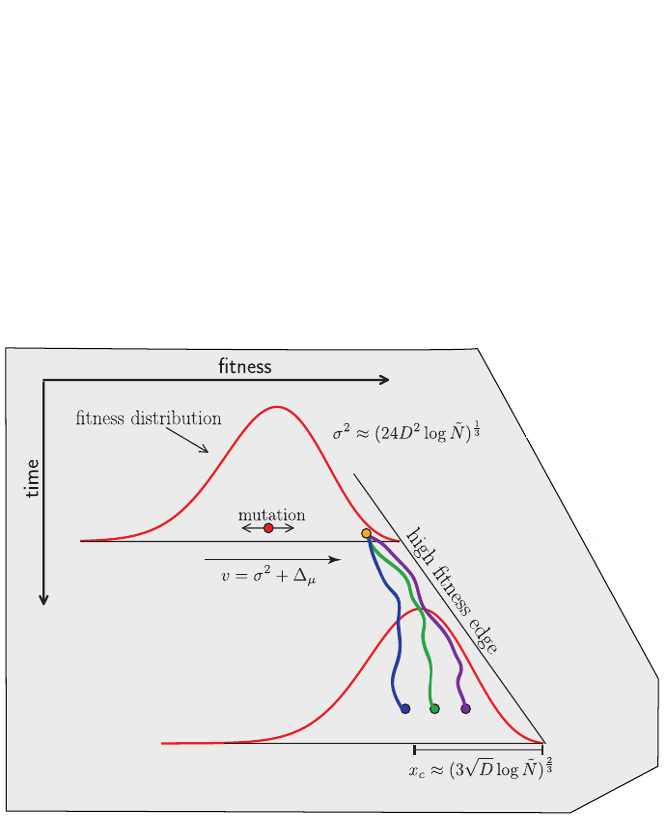
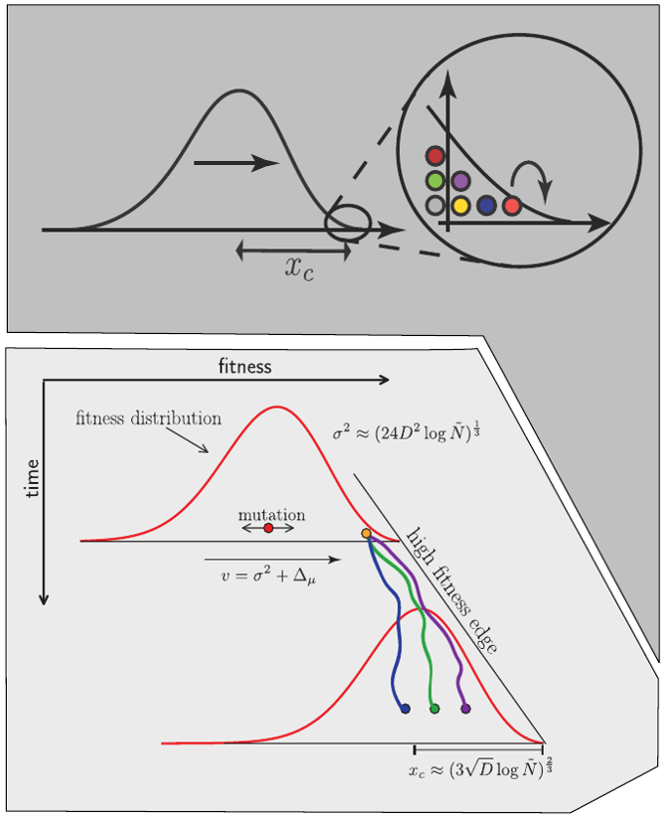
Bolthausen-Sznitman Coalescent

RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007

Bursts in a tree ↔ high fitness genotypes

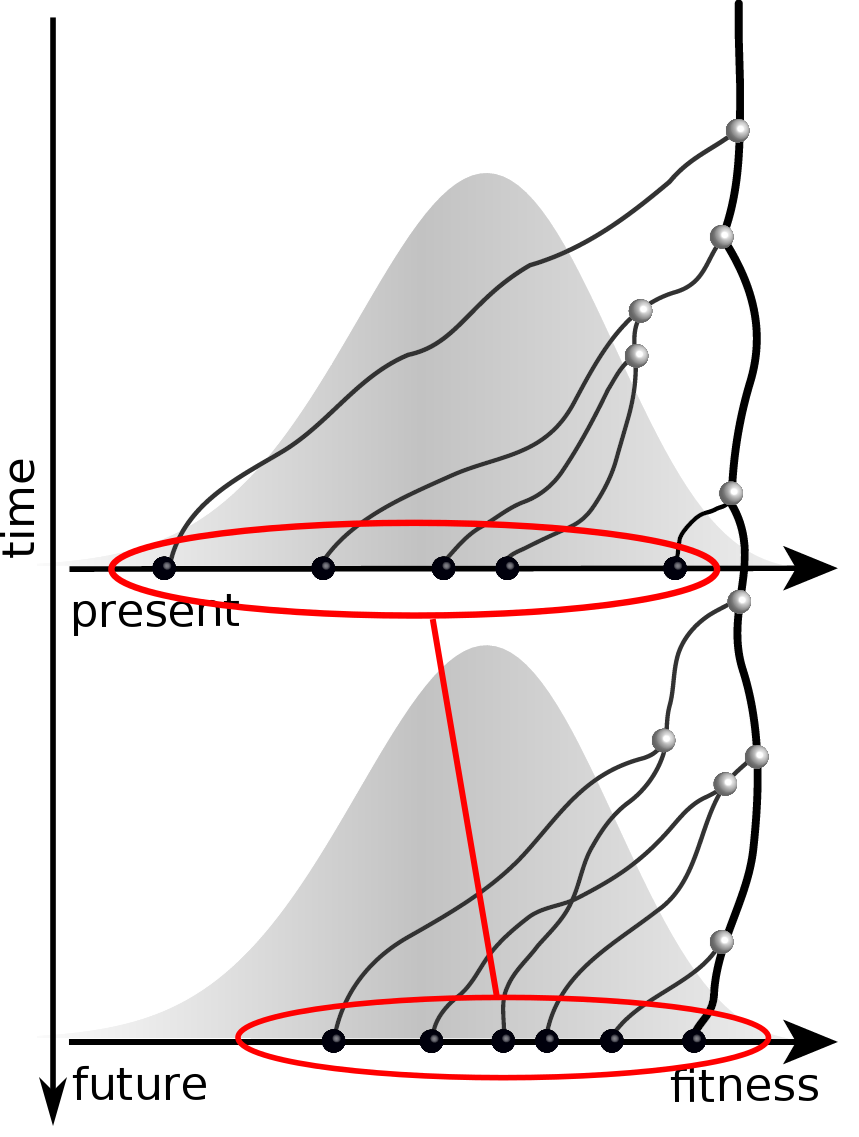
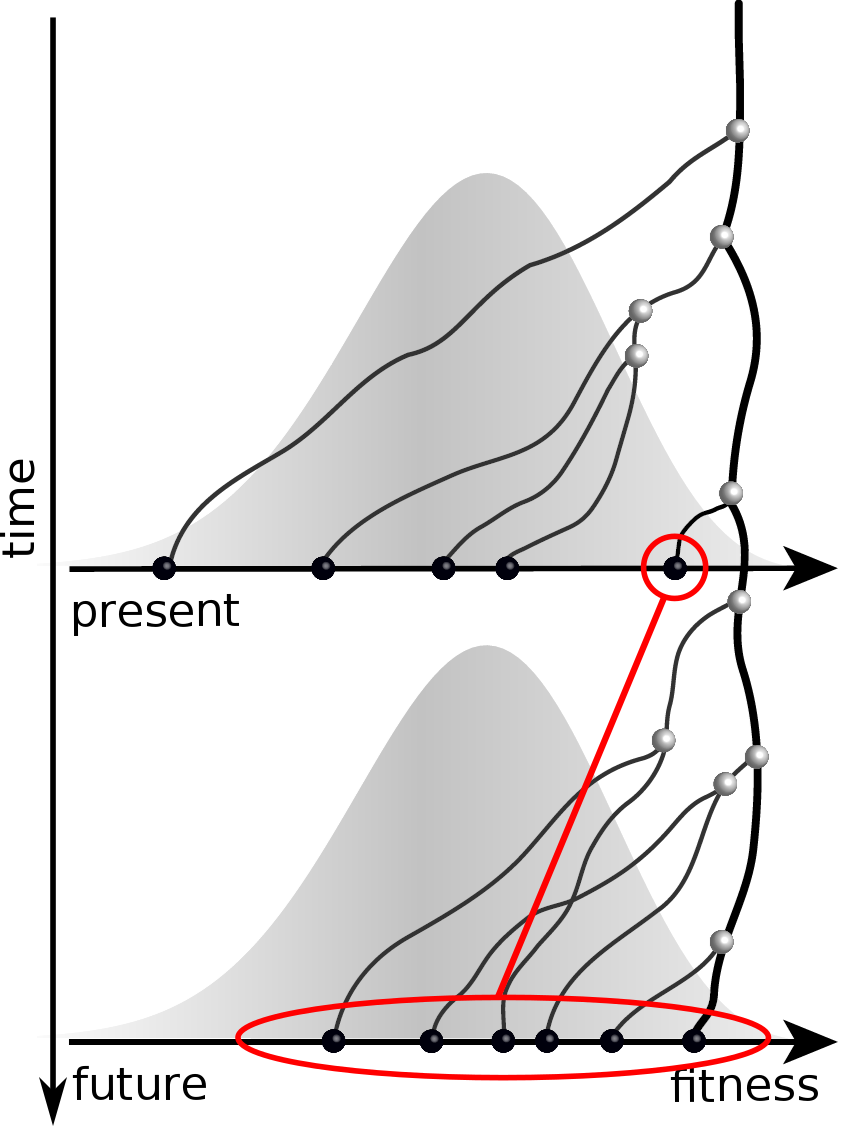
Can we read fitness of a tree?

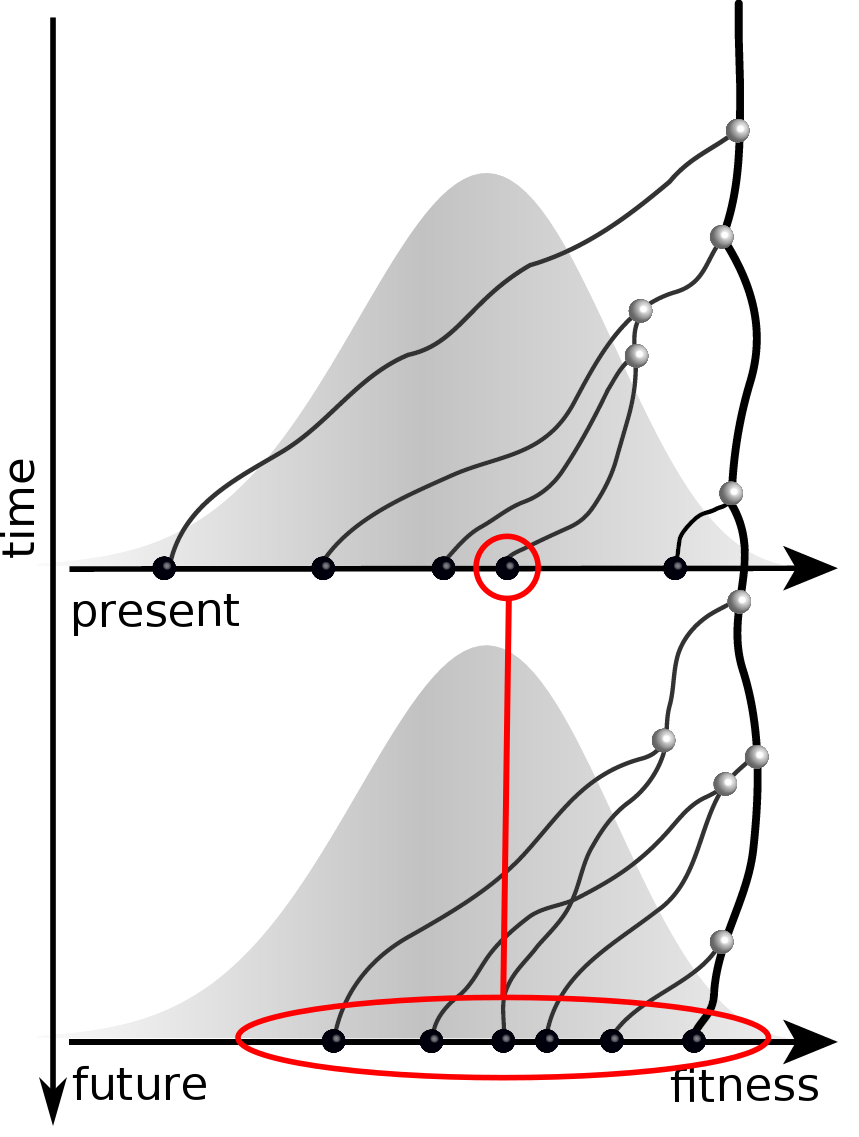
Predicting evolution

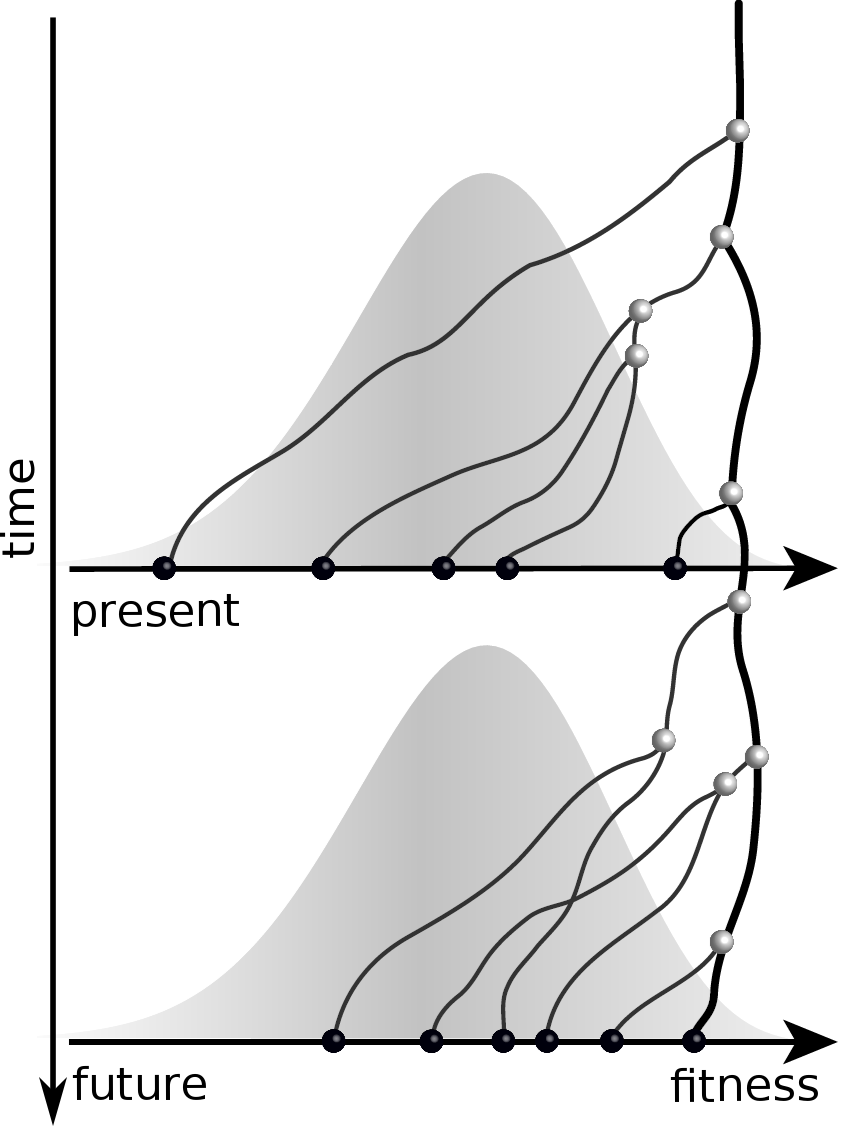
Given the branching pattern:

  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Prediction of the dominating H3N2 influenza strain

  • no influenza specific input
  • how can the model be improved? (see model by Luksza & Laessig)
  • what other context might this apply?
 RN, Russell, Shraiman, eLife, 2014

Summary

  • RNA virus evolution can be observed directly
  • Rapidly adapting population require new population genetic models
  • Those model can be used to infer fit clades
  • Future influenza population can be anticipated
  • Automated real-time analysis can help fight the spread of disease

HIV acknowledgments

  • Fabio Zanini
  • Jan Albert
  • Johanna Brodin
  • Christa Lanz
  • Göran Bratt
  • Lina Thebo
  • Vadim Puller

Influenza and Theory acknowledgments

  • Boris Shraiman
  • Colin Russell
  • Trevor Bedford
  • Oskar Hallatschek

nextstrain.org

  • Trevor Bedford
  • Colin Megill
  • Pavel Sagulenko
  • Sidney Bell
  • James Hadfield
  • Wei Ding