Real time analysis and visualization of RNA virus evolution


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/201803_XLAB.html

Viruses

tobacco mosaic virus (Thomas Splettstoesser, wikipedia)

bacteria phage (adenosine, wikipedia)

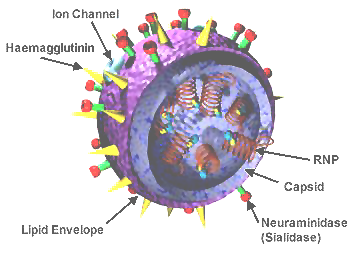
influenza virus wikipedia

human immunodeficiency virus wikipedia
  • rely on host to replicate
  • little more than genome + capsid
  • genomes typically 5-200k bases (+exceptions)
  • many infectious diseases are caused by viruses
  • very important function in microbial eco-systems
  • most abundant organisms on earth $\sim 10^{31}$

Some viruses evolve a million times faster than animals

Animal haemoglobin

HIV protein

Development of sequencing technologies

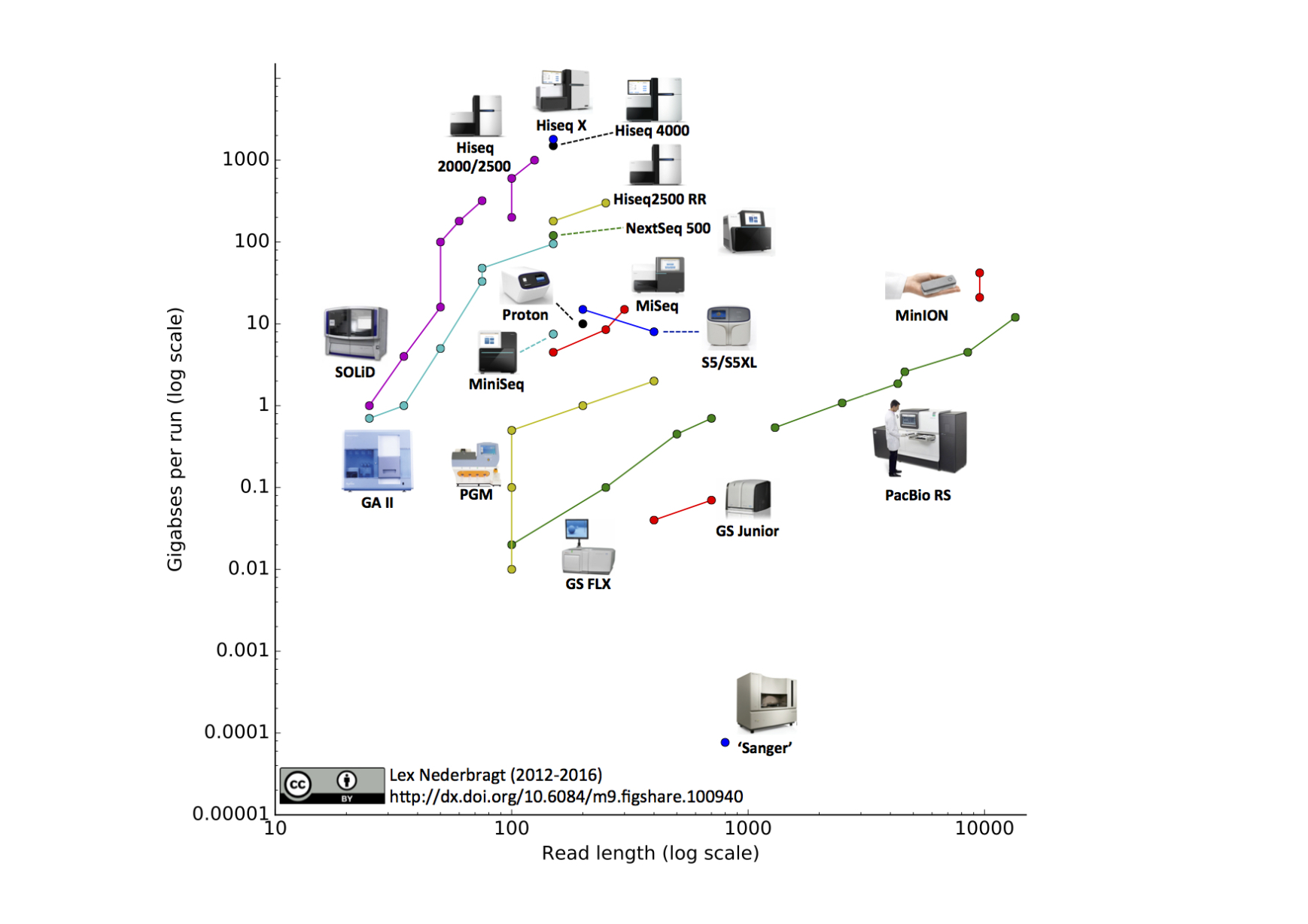
We can now sequence...
  • thousands of bacterial isolates
  • thousands of single cells
  • populations of viruses, bacteria or flies
  • diverse ecosystems

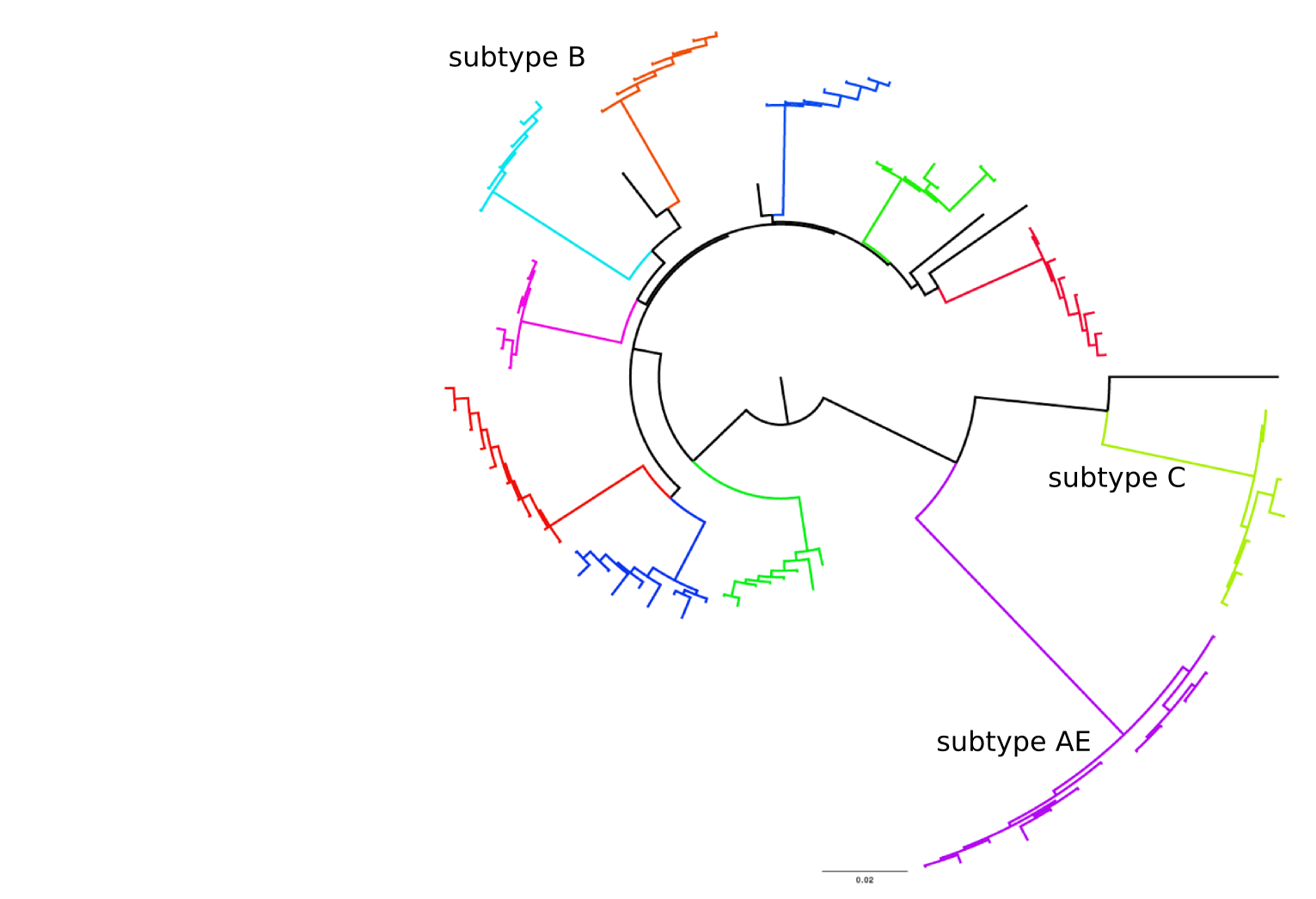
Evolution of HIV


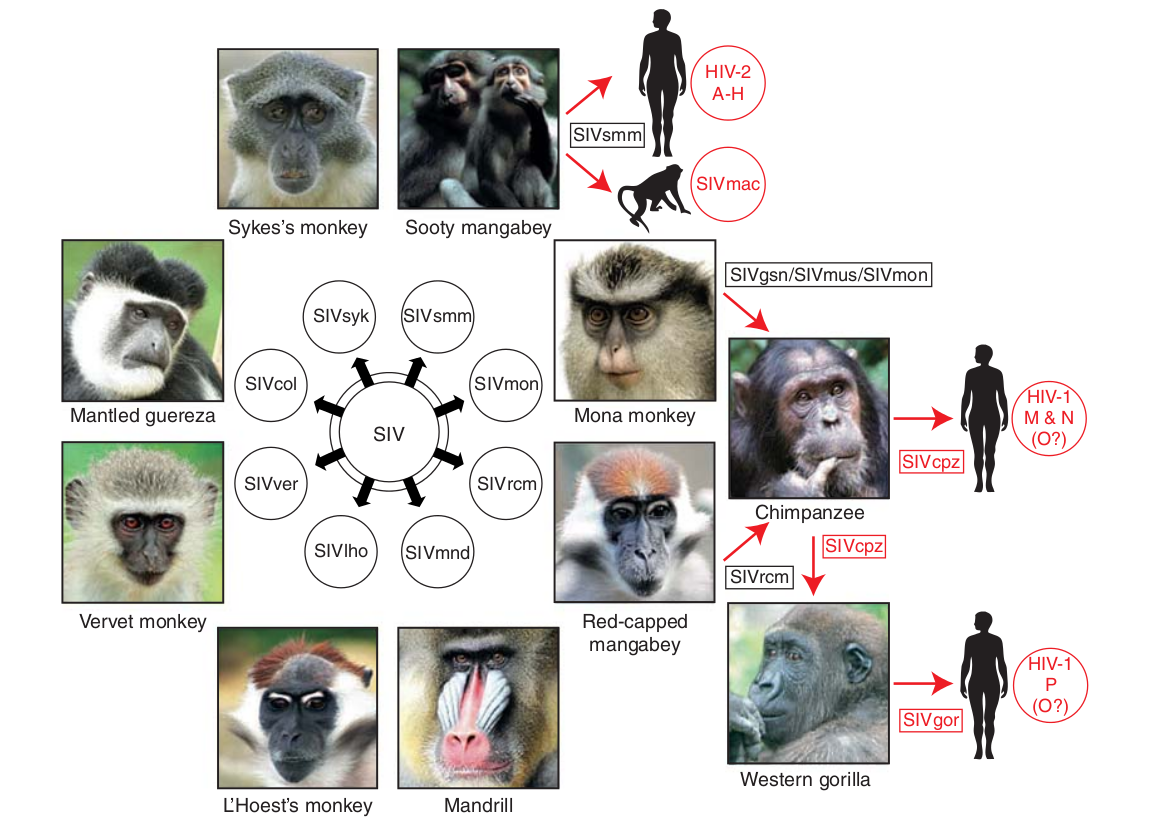
  • Chimp → human transmission around 1900 gave rise to HIV-1 group M
  • ~100 million infected people since
  • subtypes differ at 10-20% of their genome
  • HIV-1 evolves ~0.1% per year
image: Sharp and Hahn, CSH Persp. Med.

HIV infection

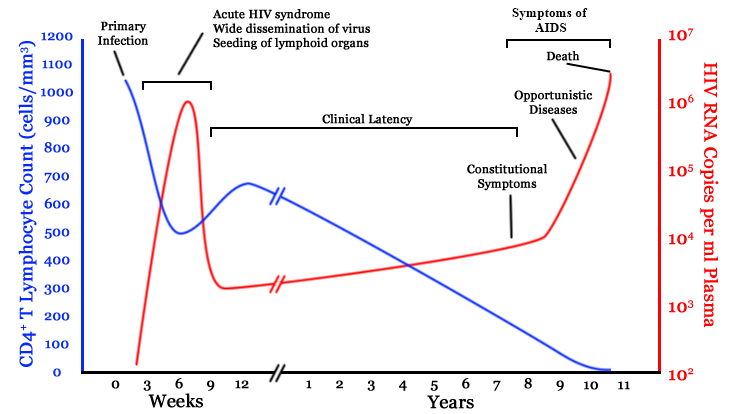
  • $10^8$ cells are infected every day
  • the virus repeatedly escapes immune recognition
  • integrates into T-cells as latent provirus
image: wikipedia

HIV-1 evolution within one individual



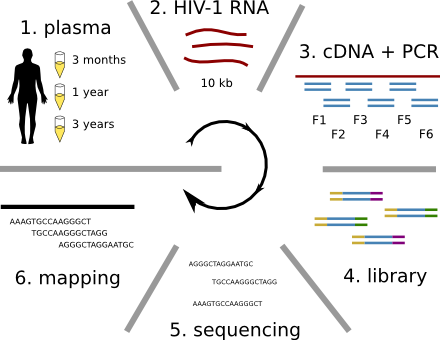
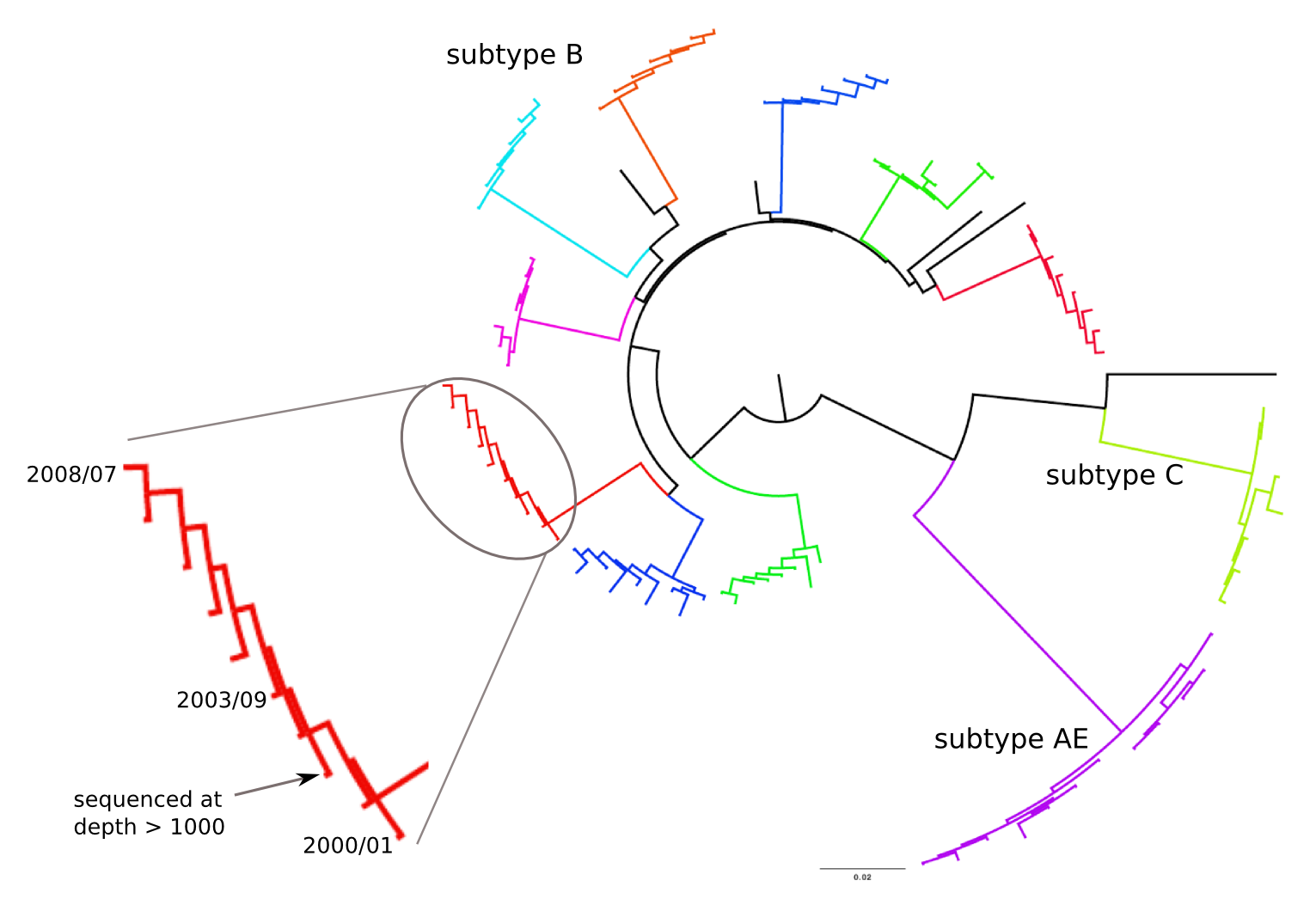
silouhette: clipartfest.com, Zanini at al, 2015. Collaboration with Jan Albert and his group


Immune escape in early HIV infection

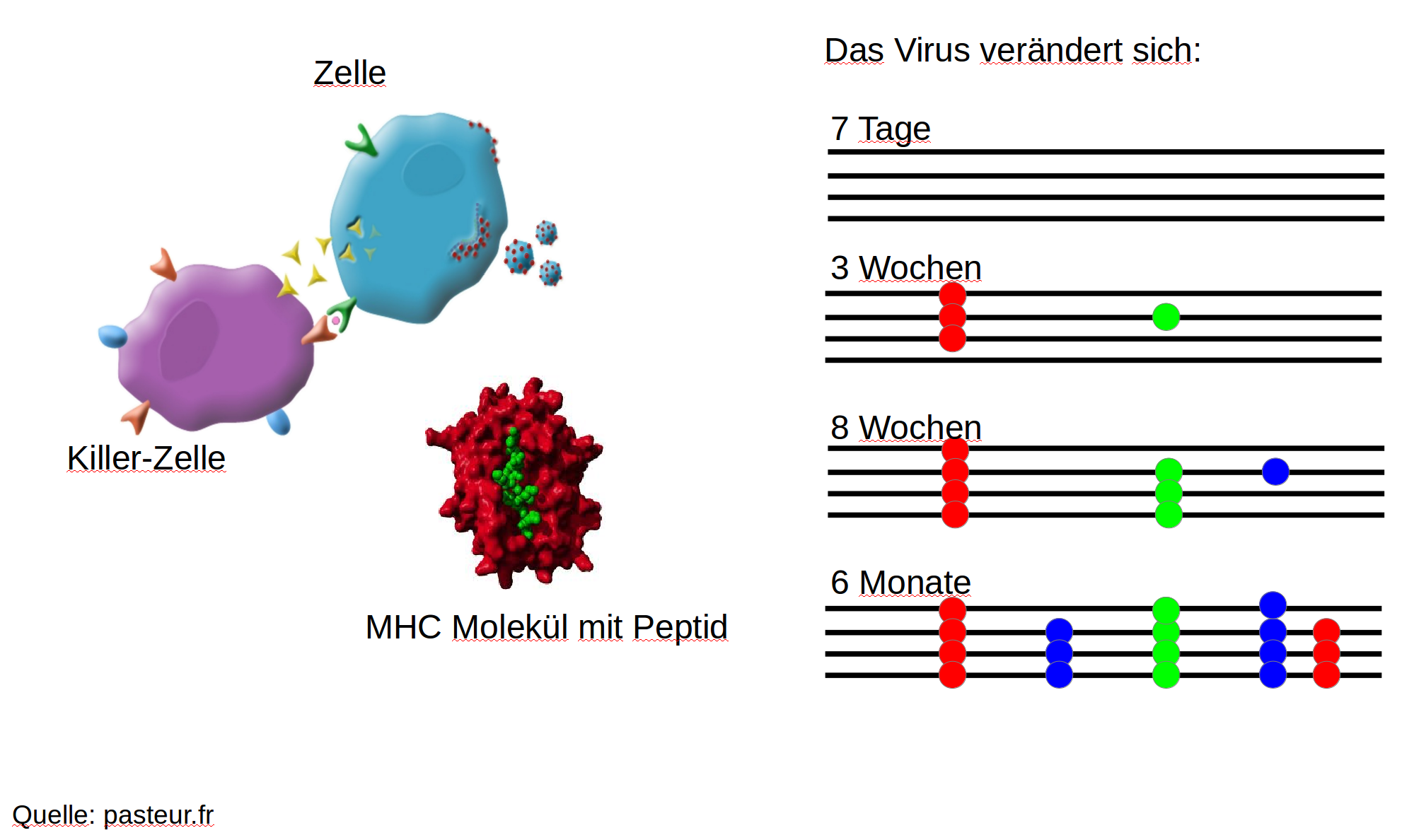
Immune escape in early HIV infection

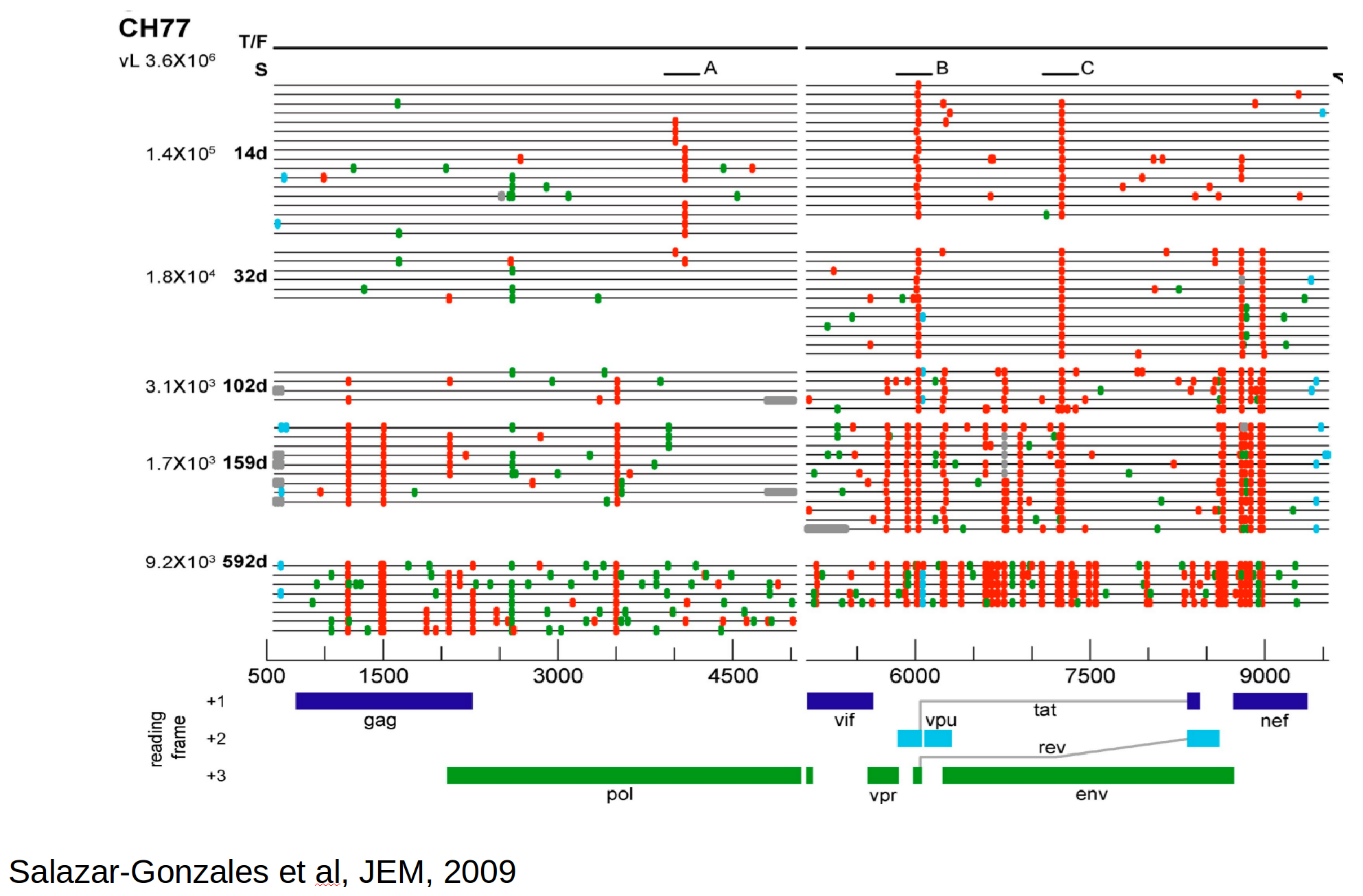
Population genetics & evolutionary dynamics

evolutionary processes ↔ trees ↔ genetic diversity

Selective sweeps

  • Viruses carrying a beneficial mutation have more offspring: on average $1+s$ instead of $1$
  • $s$ is called selection coefficient
  • Fraction $x$ of viruses carrying the mutation changes as $$x(t+1) = \frac{(1+s)x(t)}{(1+s)x(t) + (1-x(t))}$$
  • In continuous time → logistic differential equation: $$\frac{dx}{dt} = sx(1-x) \Rightarrow x(t) = \frac{e^{s(t-t_0)}}{1+ e^{s(t-t_0)}}$$

Population sequencing to track all mutations above 1%

  • diverge at 0.1-1% per year
  • almost whole genome coverage in 10 patients
  • full data set at hiv.tuebingen.mpg.de
Zanini et al, eLife, 2015; antibody data from Richman et al, 2003

The rate of sequence evolution in HIV

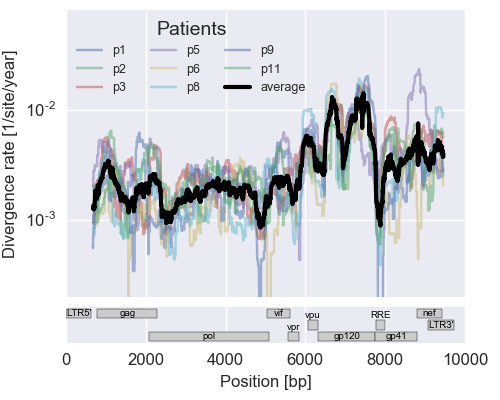
Evolution in different parts of the genome

  • envelope changes fastest, enzymes lowest
  • identical rate of synonymous evolution
  • diversity saturates where evolution is fast
  • synonymous mutations stay at low frequency
Zanini et al, eLife, 2015

Mutation rates and diversity and neutral sites

Zanini et al, Virus Evolution, 2017

Inference of fitness costs

  • mutation away from preferred state with rate $\mu$
  • selection against non-preferred state with strength $s$
  • variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
  • equilibrium frequency: $\bar{x} = \mu/s $
  • fitness cost: $s = \mu/\bar{x}$

Fitness landscape of HIV-1

Zanini et al, Virus Evolution, 2017

Selection on RNA structures and regulatory sites

Zanini et al, Virus Evolution, 2017

The distribution of fitness costs

Zanini et al, Virus Evolution, 2017

Sequences record the spread of pathogens

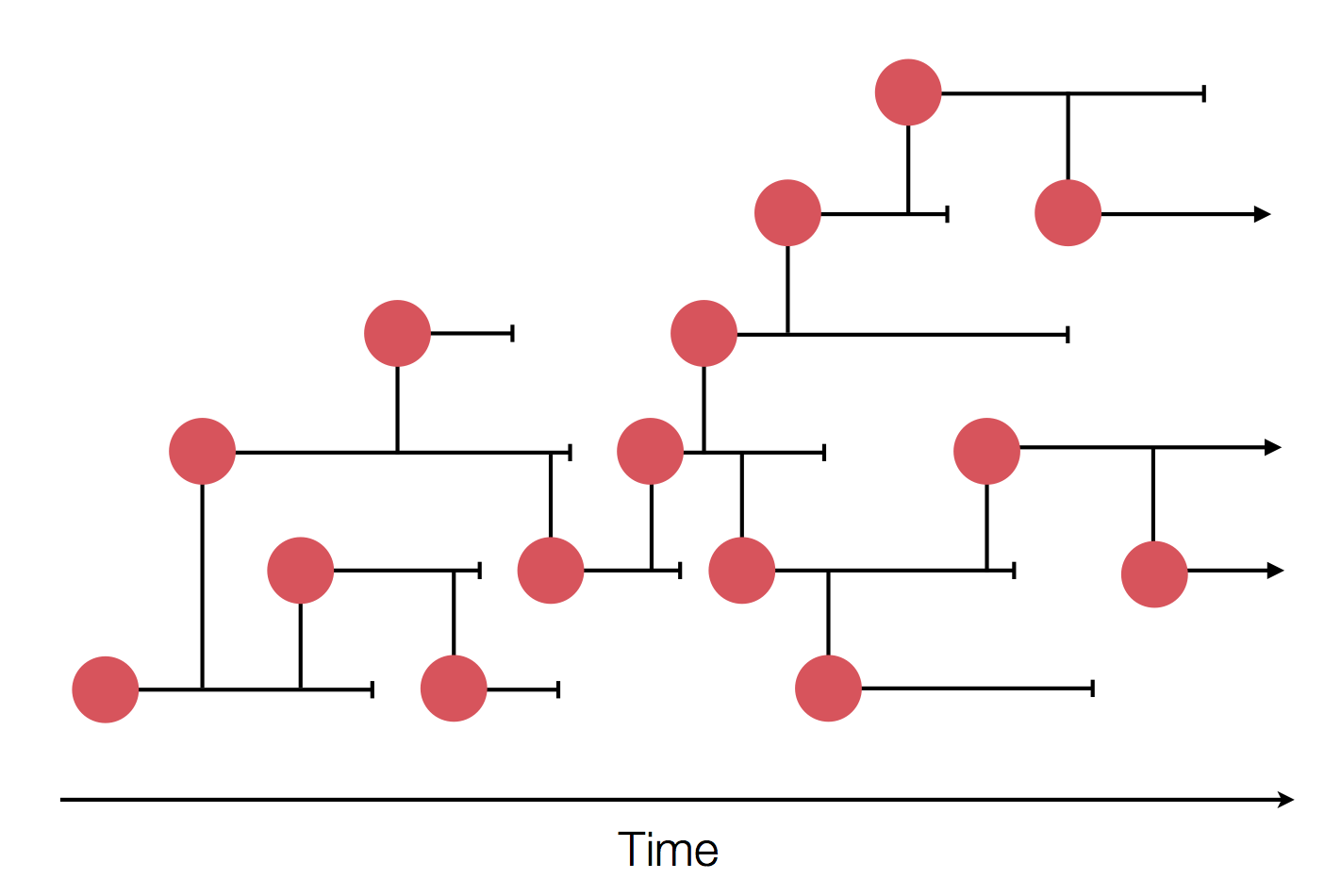
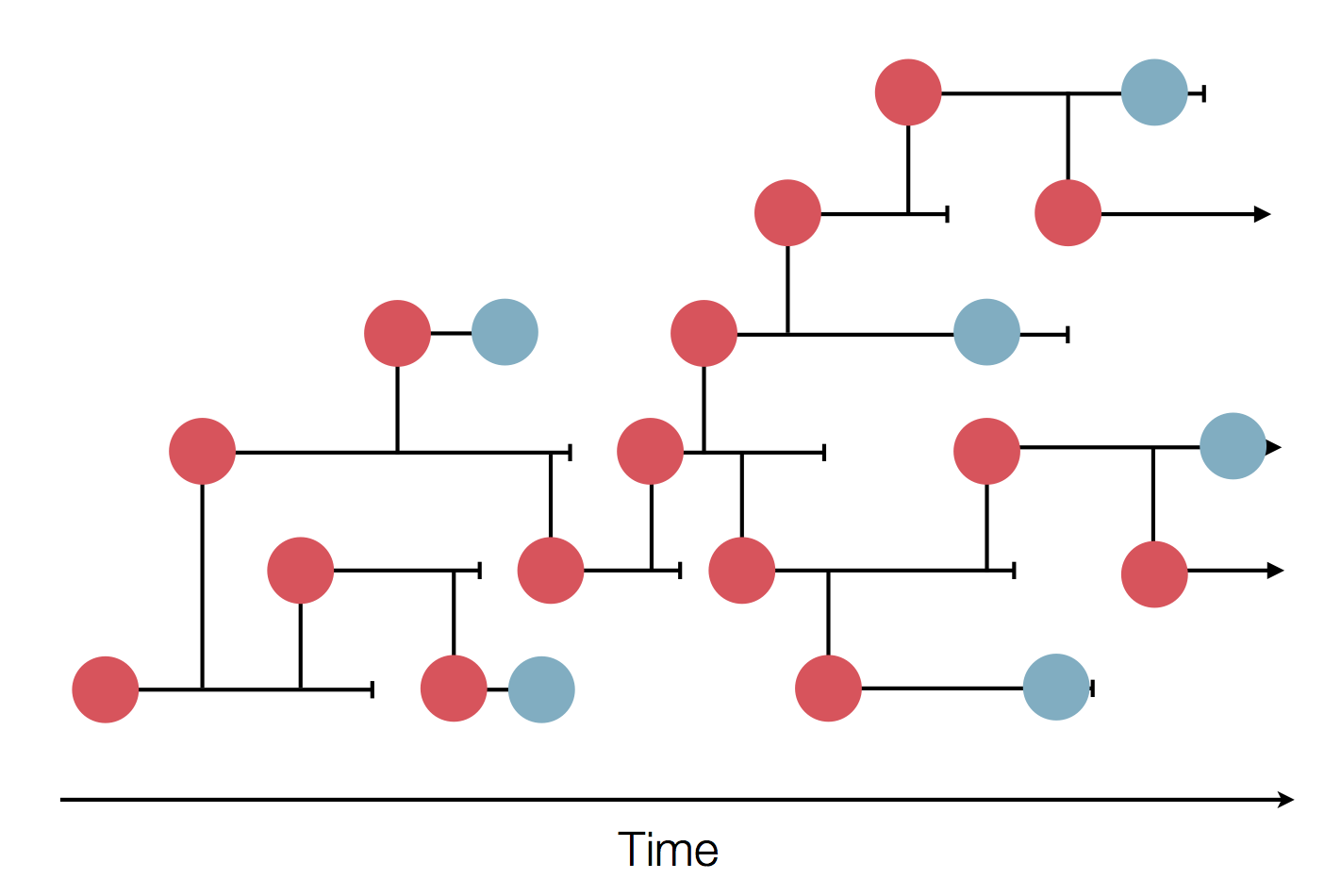
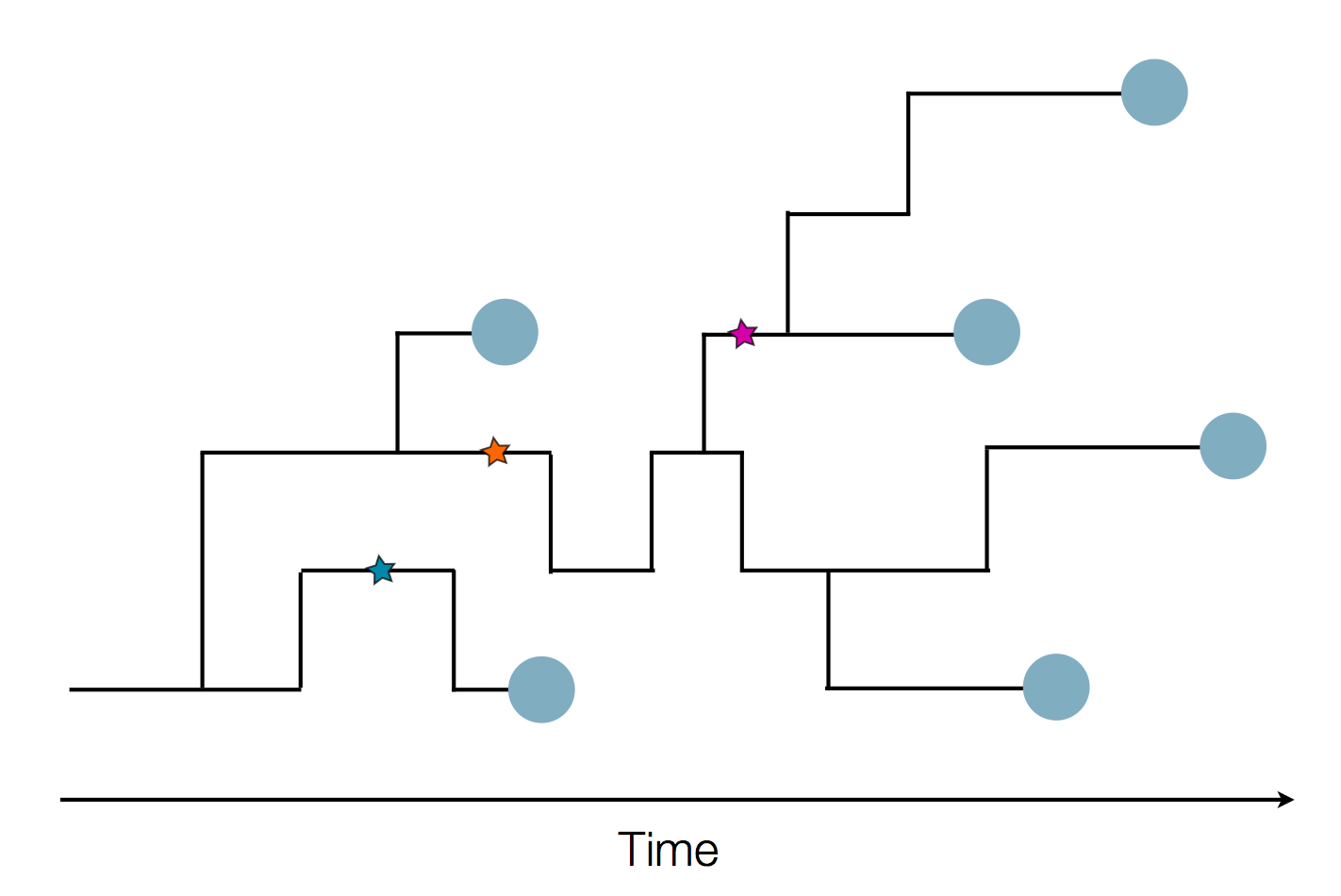
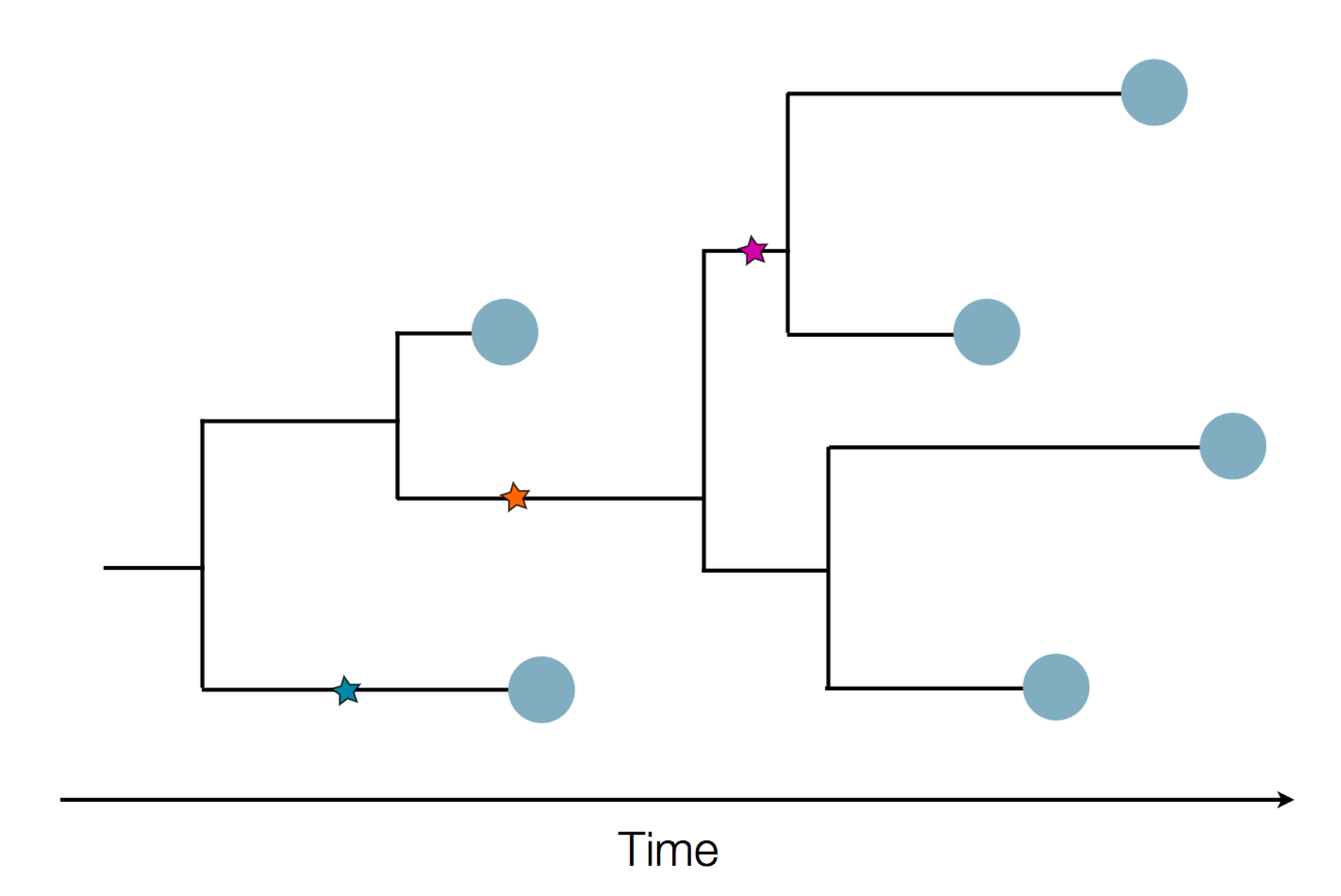
The resolution is limited by the number of mutations!
images by Trevor Bedford

Influenza virus genome - 8 segments

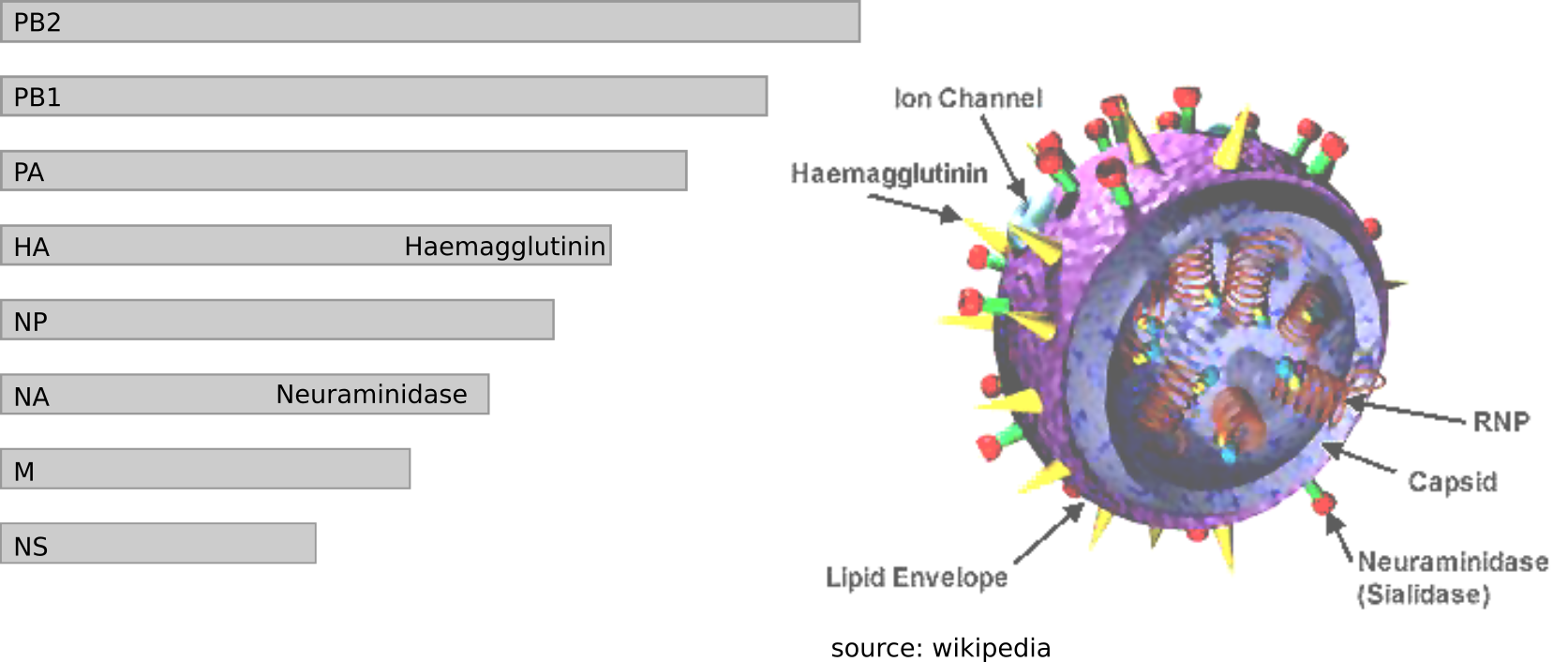
Zika virus genome $\sim 10000$ bases

Ebola virus genome $\sim 20000$ bases

Many RNA viruses pick up one mutation every 2-4 weeks!

Human seasonal influenza viruses

slide by Trevor Bedford


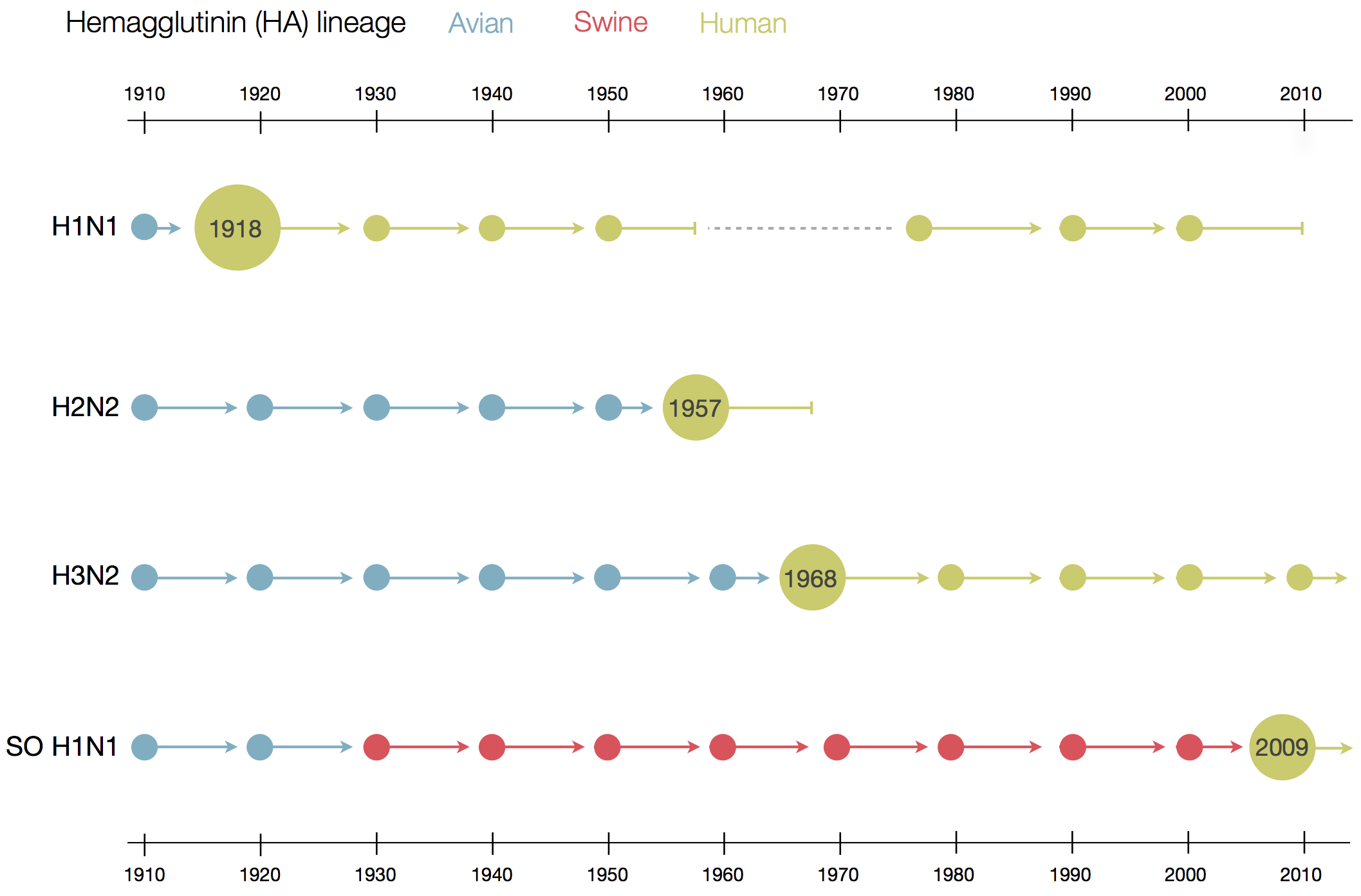
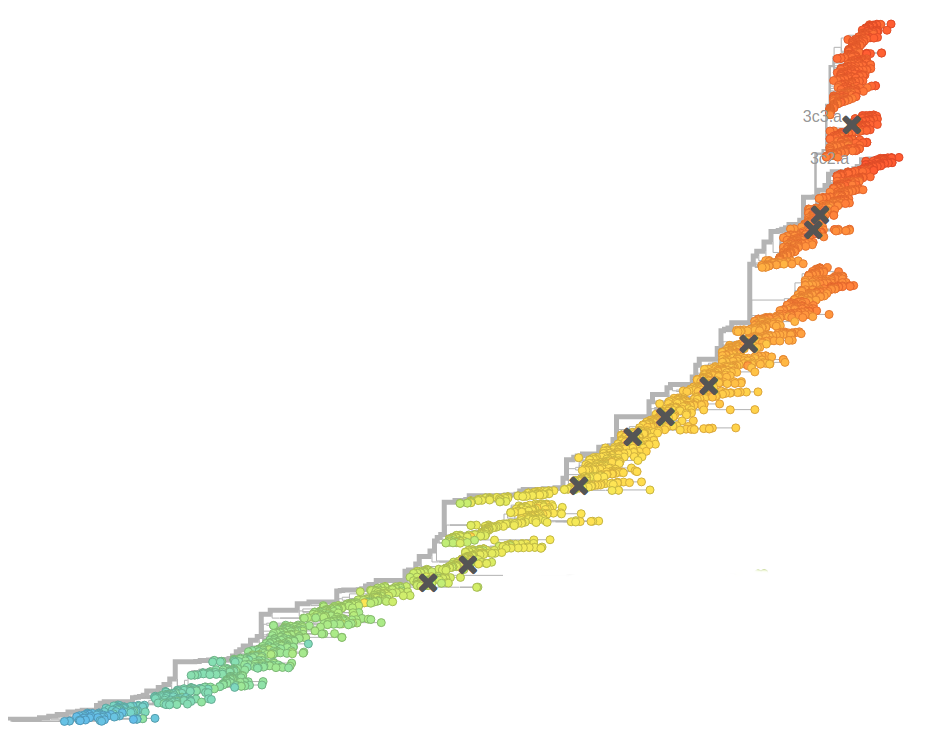
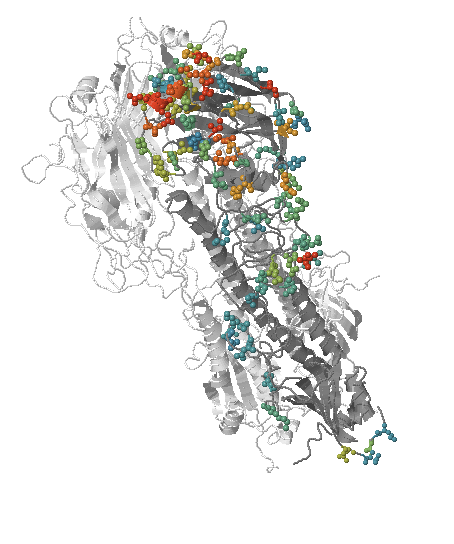
  • Influenza viruses evolve to avoid human immunity
  • Vaccines need frequent updates

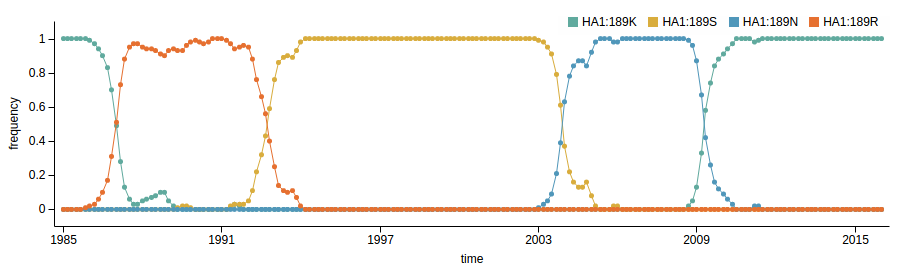
nextflu.org

joint work with Trevor Bedford & his lab

code at github.com/blab/nextflu

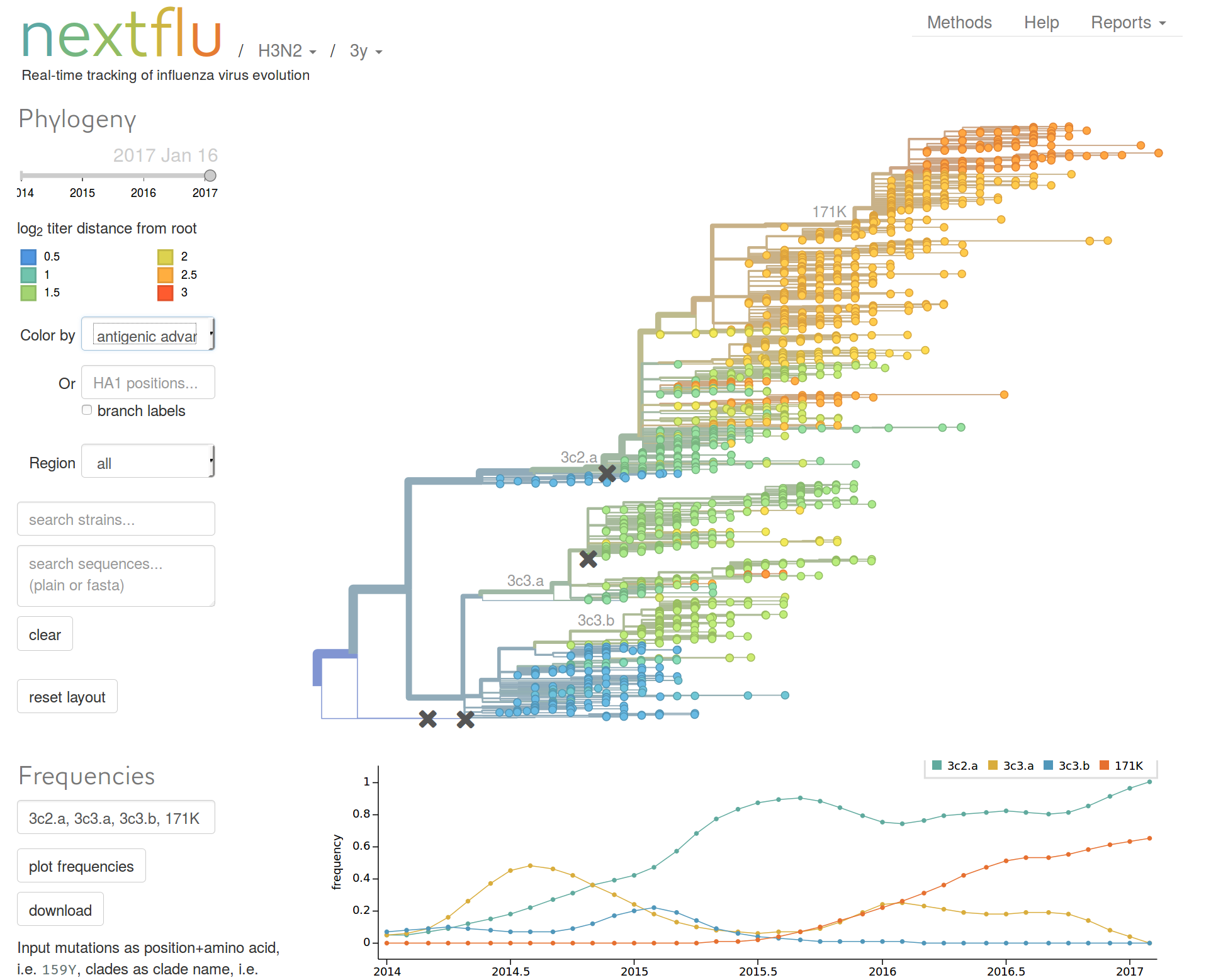
Predicting evolution

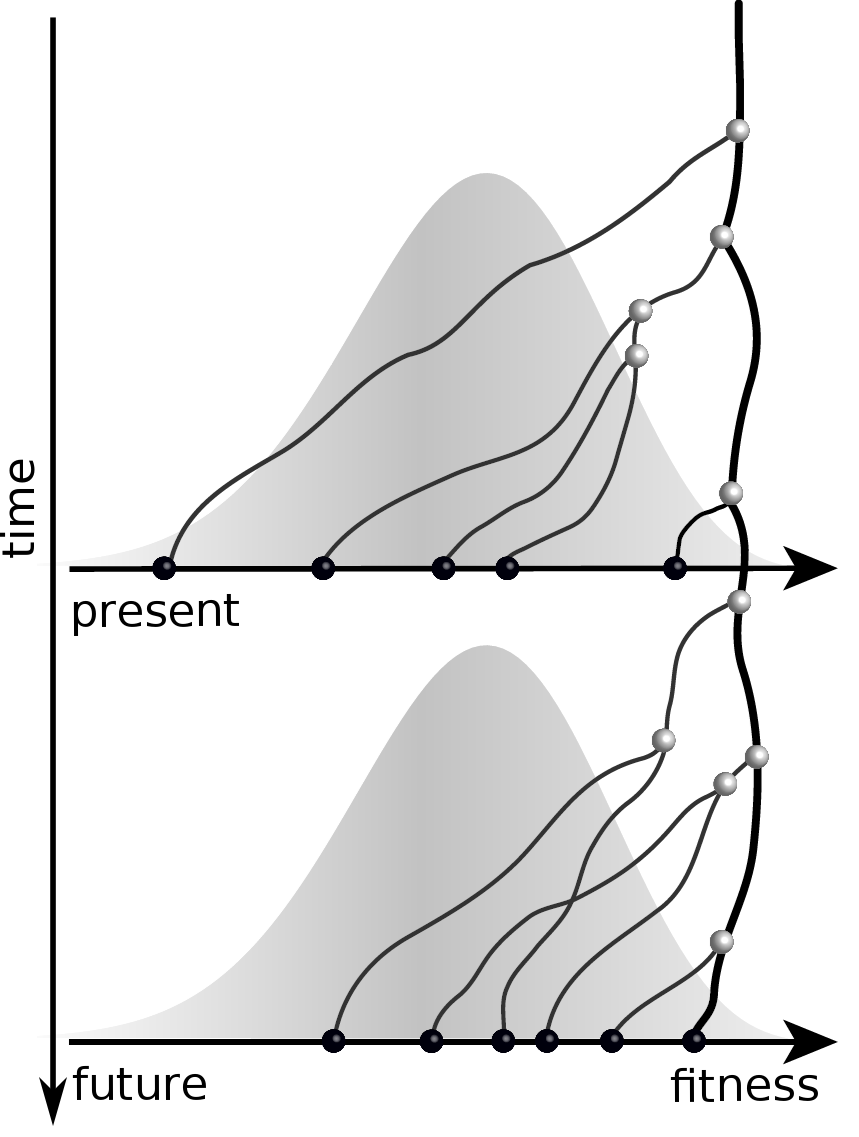
Given the branching pattern:

  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014

Validate on simulation data

  • simulate evolution
  • sample sequences
  • reconstruct trees
  • infer fitness
  • predict ancestor of future
  • compare to truth
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Prediction of the dominating H3N2 influenza strain

  • no influenza specific input
  • how can the model be improved? (see model by Luksza & Laessig)
  • what other context might this apply?
 RN, Russell, Shraiman, eLife, 2014

Sequence alignment?

Reconstruction of phylogenetic trees

  • There are super-exponentially many trees
  • for $n$ taxa, there are $N = (2n-5)!! = (2n-5)*(2n-7)*\cdots*3*1$ trees
  • There are efficient heuristics to reconstruct trees, e.g. Neighbor Joining

nextstrain.org

joint work with Trevor Bedford & his lab

code at github.com/nextstrain

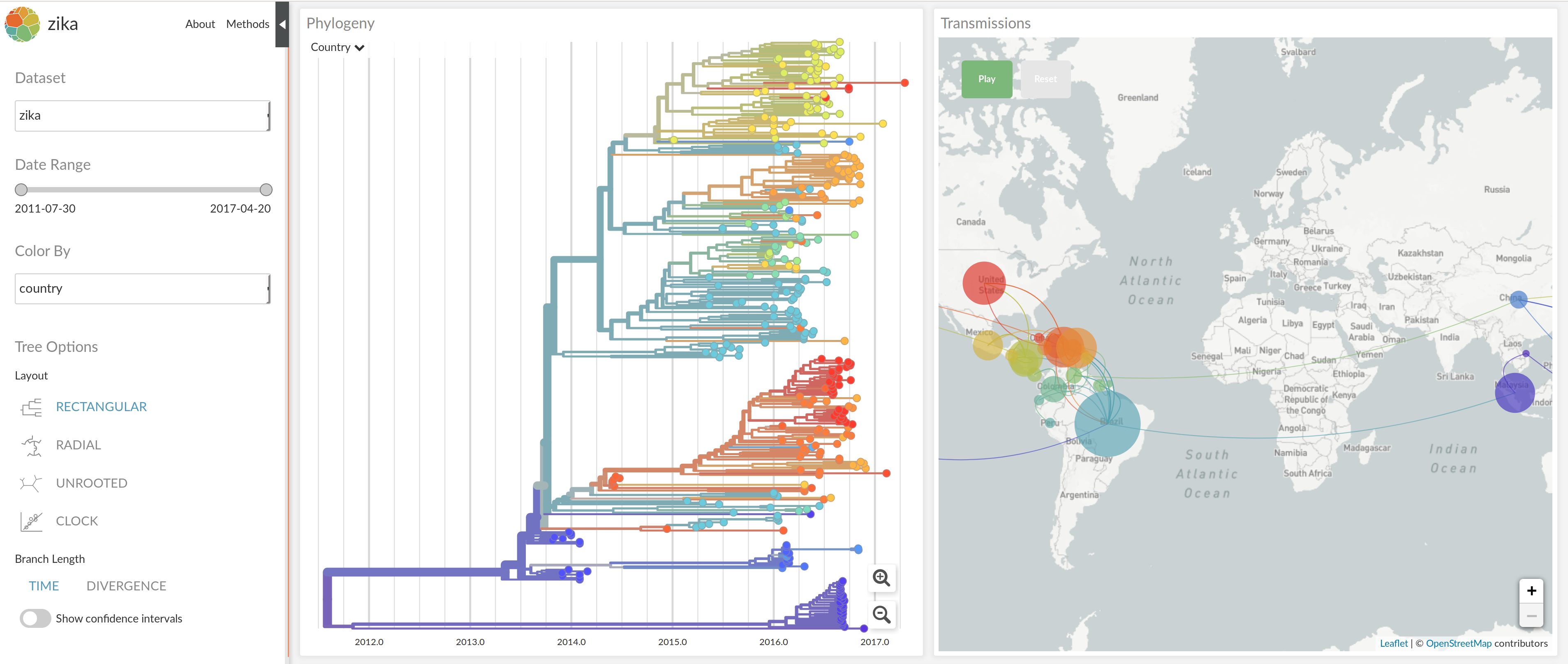
NextStrain architecture

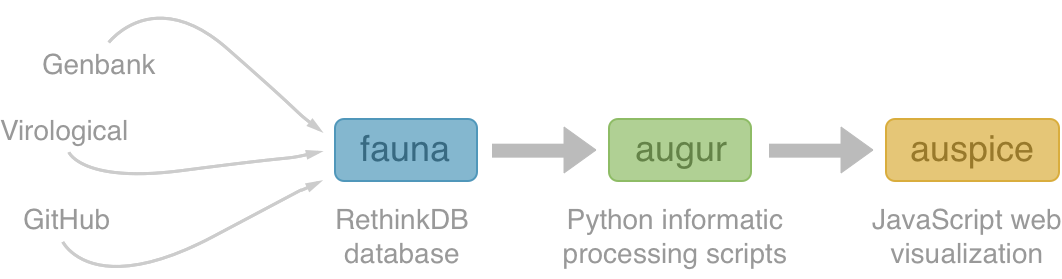
Using treetime to rapidly compute timetrees

TreeTime: maximum likelihood phylodynamic analysis

Phylogenetic trees record history:
  • transmission
  • divergence times
  • population dynamics
  • ancestral geographic distribution/migrations
Typical approach: Bayesian parameter estimation
  • flexible
  • probabilistic → confidence intervals etc
  • but: computationally expensive
TreeTime by Pavel Sagulenko
  • probabilistic treatment of divergence times
  • dates trees with thousand sequences in a few minutes
  • linear time complexity
  • fixed tree topology
  • github.com/neherlab/treetime
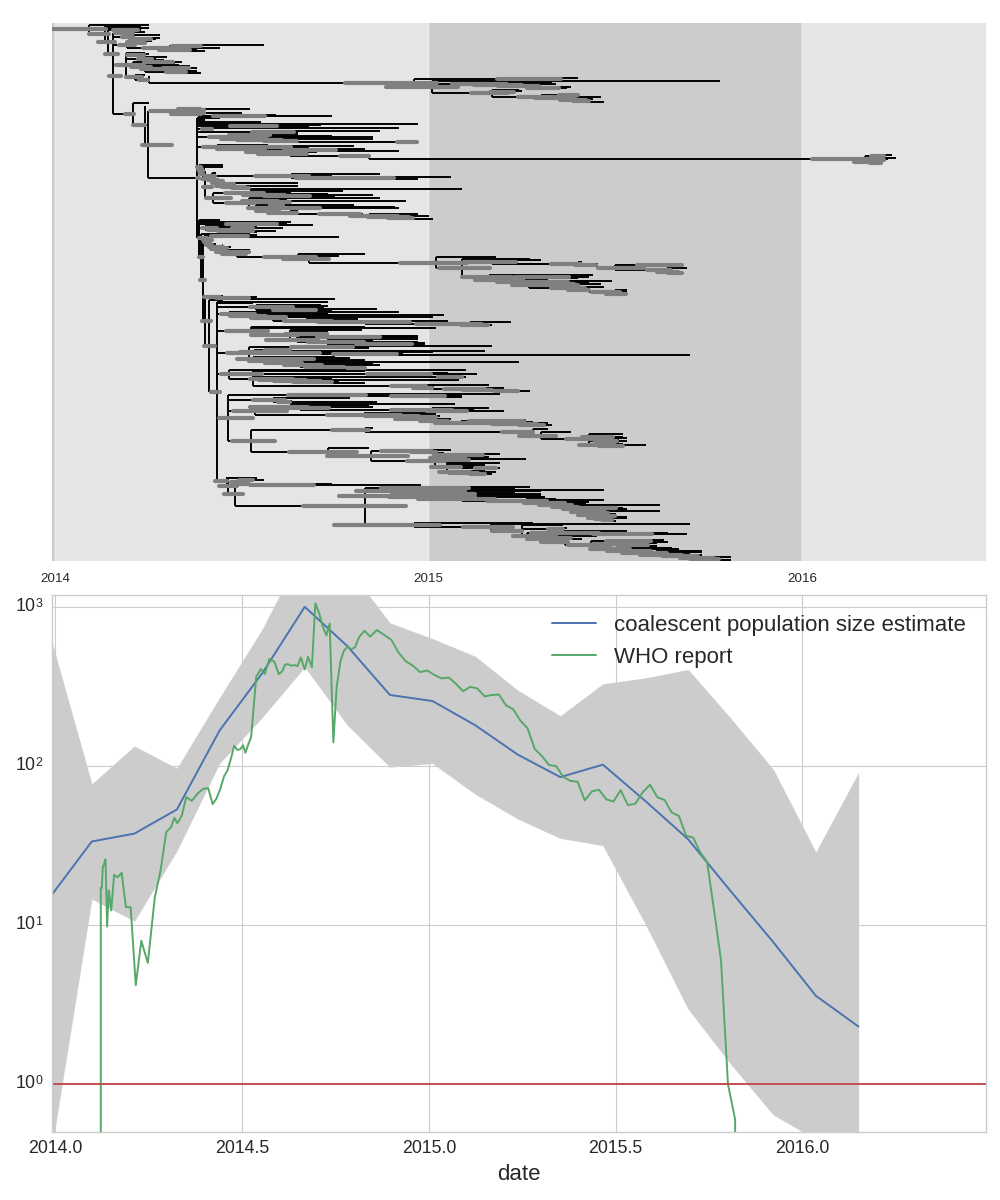
West African Ebola virus outbreak

TreeTime: nuts and bolts

Attach sequences and dates
Reconstruct ancestral sequences
Propagate temporal constraints via convolutions
Integrate up-stream and down-stream constraints
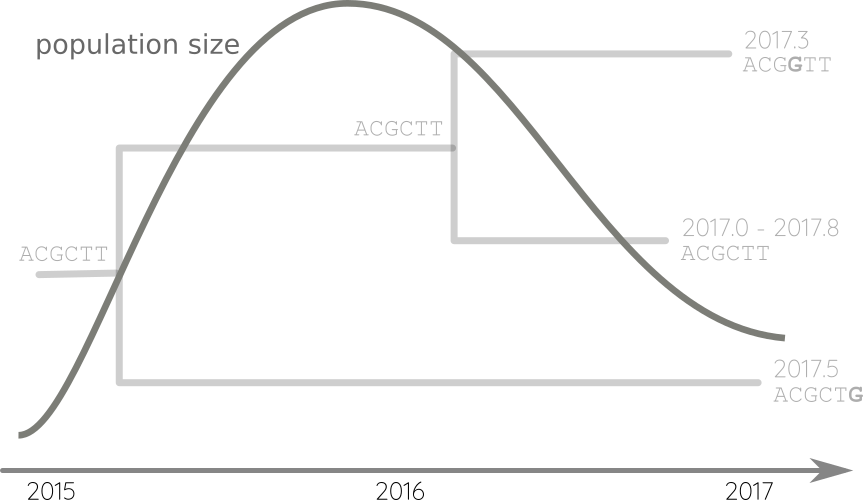
Fit phylodynamic model → iterate

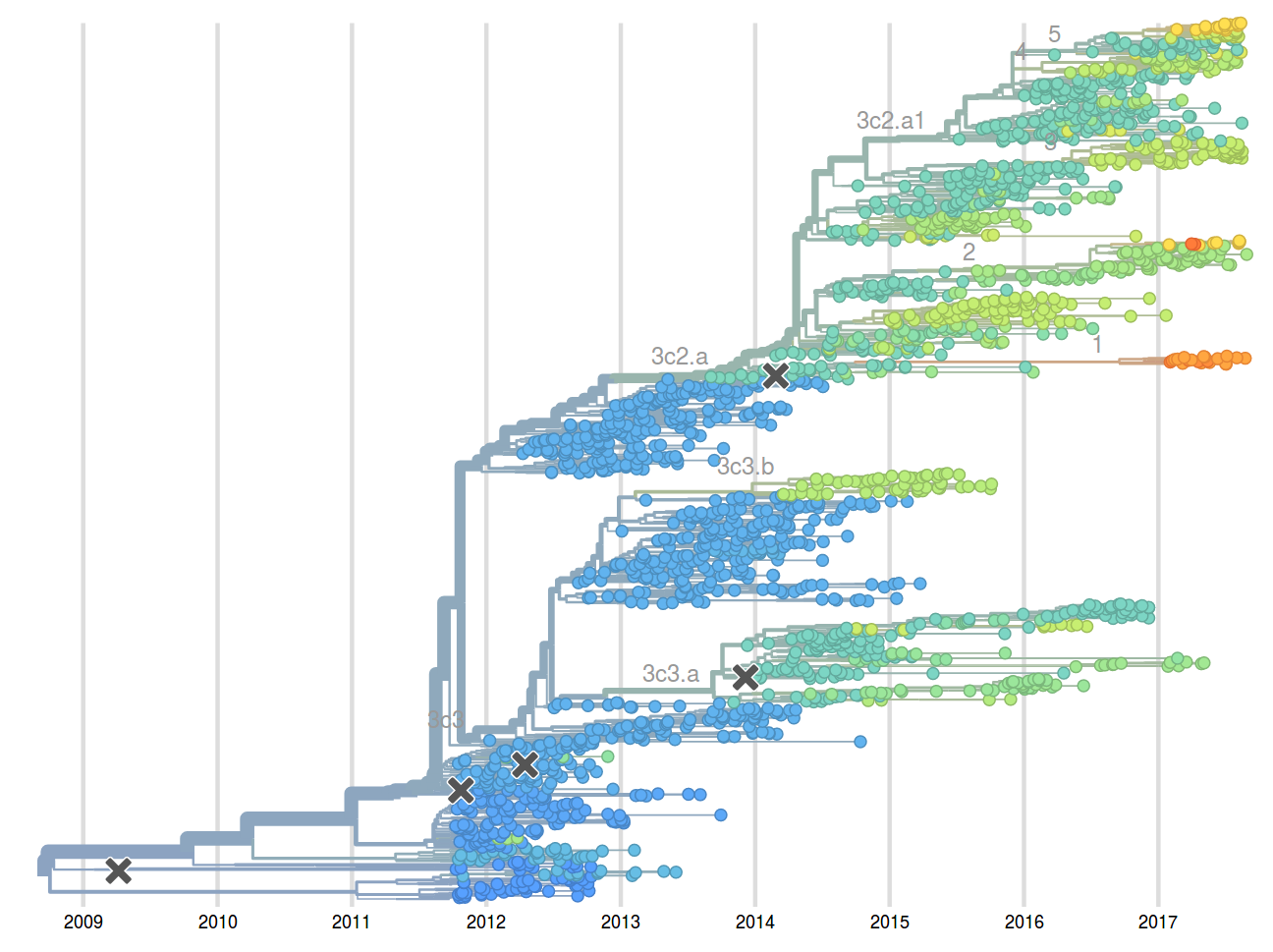
Molecular clock phylogenies of ~2000 A/H3N2 HA sequences -- a few minutes

What about bacteria?

  • vertical and horizontal transmission
  • genome rearrangements
  • much larger genomes
  • variation of divergence along the genome
  • NGS genomes tend to be fragmented
  • annotations of variable quality
panX by Wei Ding
  • pan-genome identification pipeline
  • phylogenetic analysis of each orthologous cluster
  • detect associations with phenotypes
  • fast: analyze hundreds of genomes in a few hours
  • github.com/neherlab/pan-genome-analysis

panX @ pangenome.de

S. pneumoniae data set by Croucher et al.

Pan-genome statistics and filters

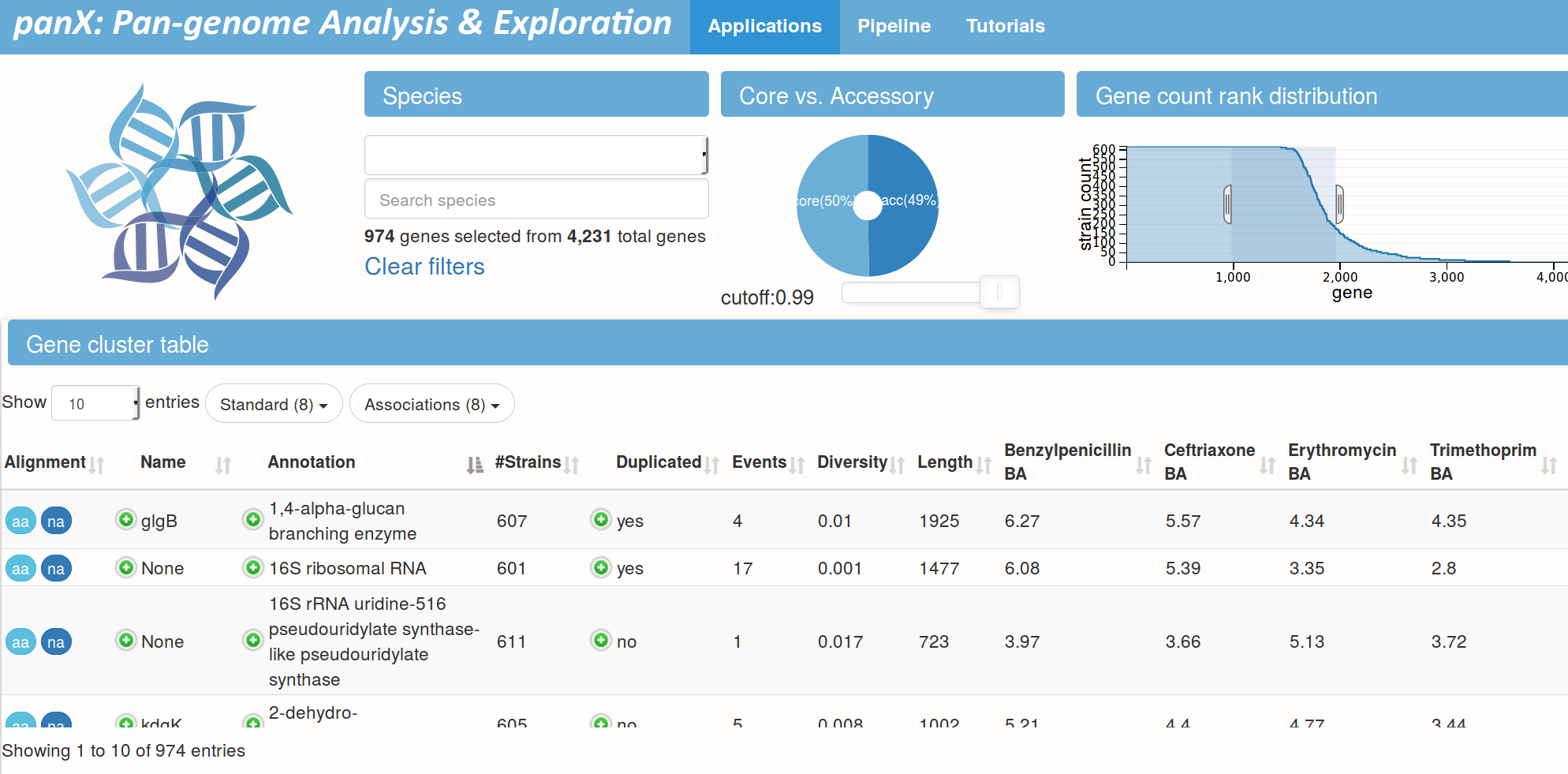
Species trees and gene trees

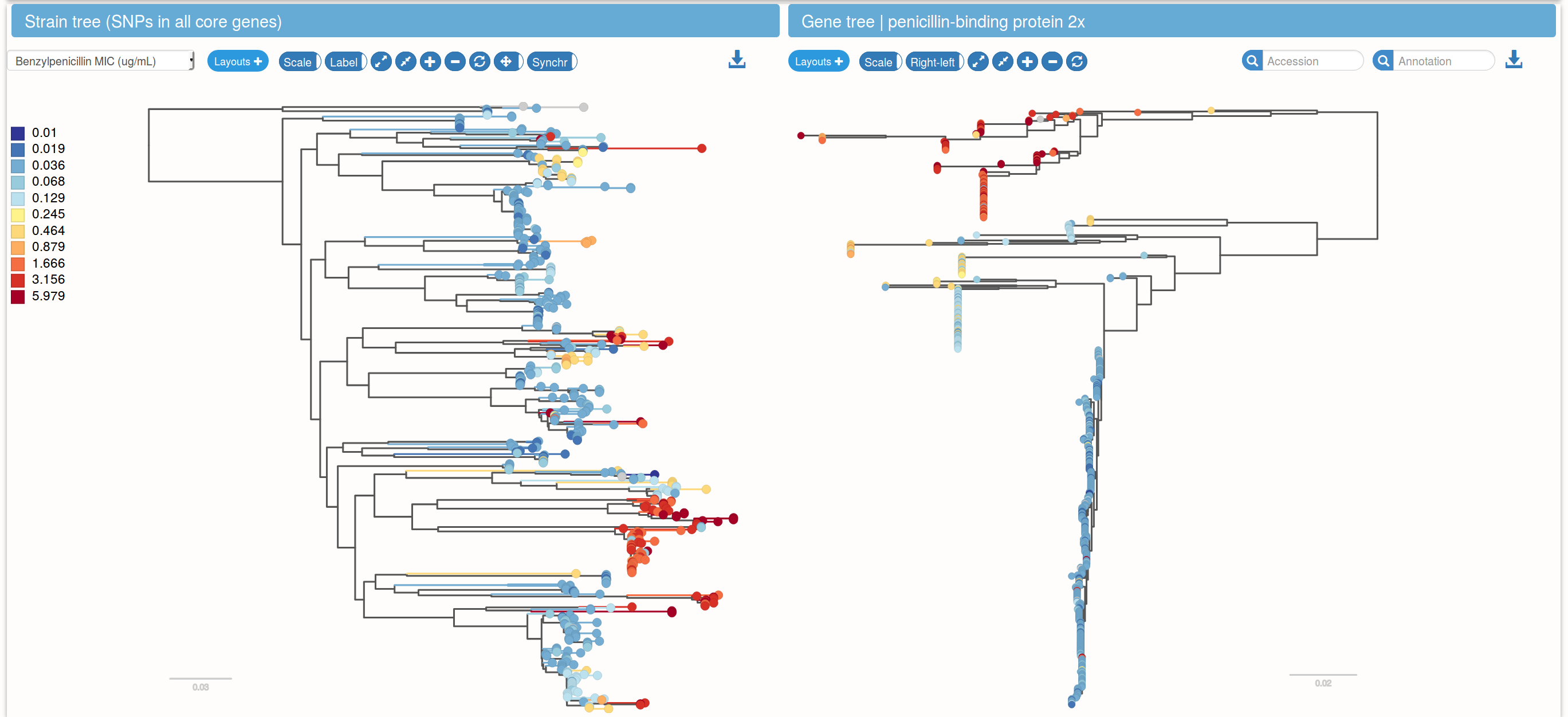
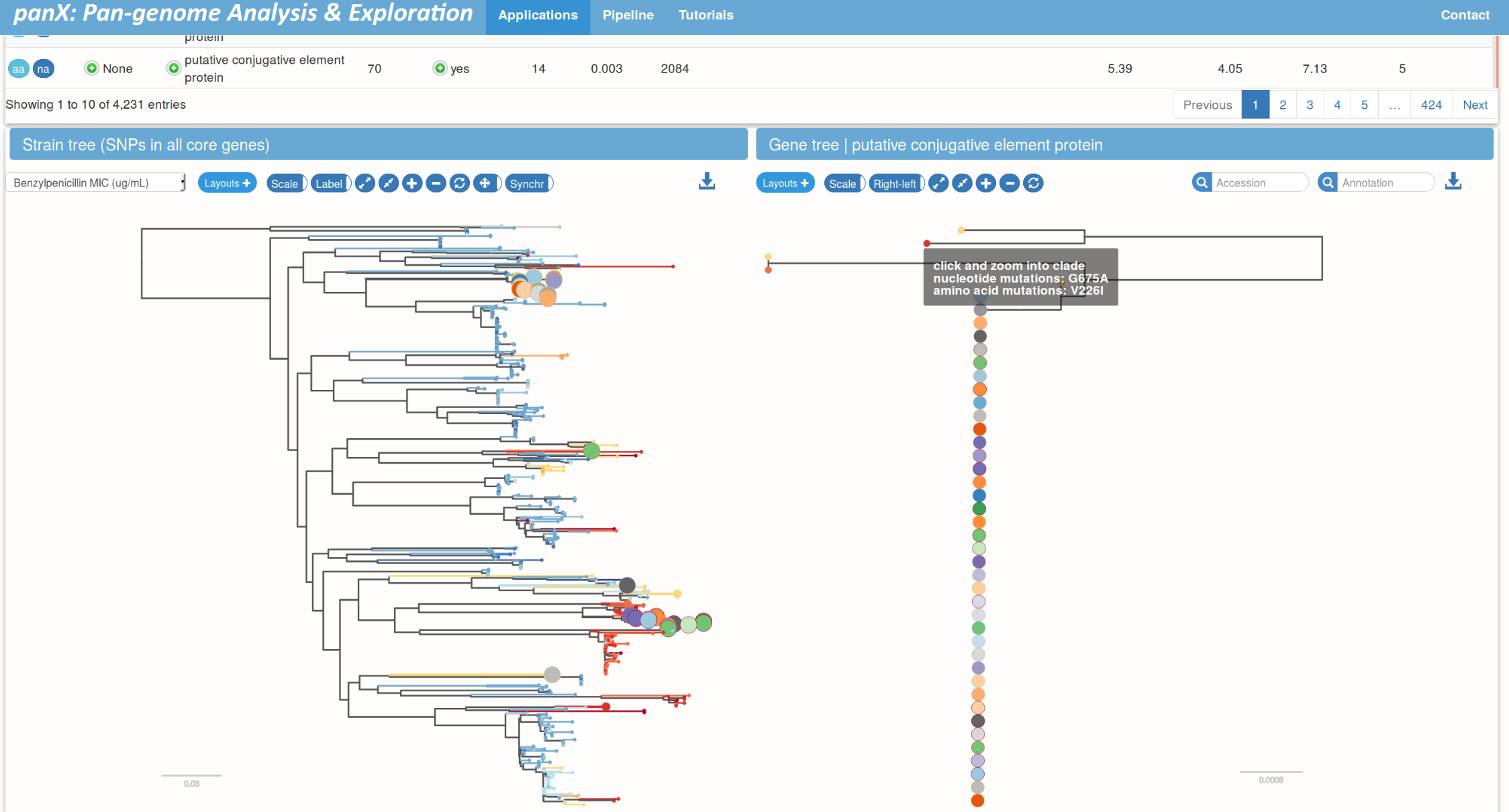
Links between species trees and gene trees

Summary

  • Data set are growing rapidly
    → tools for interpretation and exploration are crucial
  • Breadth and depth
    → provide an overview, integrate, and go deep
  • Actionable outputs require (near)real-time analysis
    → fast analysis pipelines are essential
  • We are just scratching the surface...

Interested in HIV NGS: come find me!

Influenza and Theory acknowledgments

  • Boris Shraiman
  • Colin Russell
  • Trevor Bedford
  • Oskar Hallatschek

  • All the NICs and WHO CCs that provide influenza sequence data

nextstrain.org

  • Trevor Bedford
  • Colin Megill
  • Sidney Bell
  • James Hadfield

  • All the scientist that share virus sequence data

TreeTime & panX

TreeTime: Pavel Sagulenko

github.com/neherlab/treetime
webserver at treetime.ch
manuscript on bioRxiv
panX: Wei Ding
github.com/neherlab/pan-genome-analysis
live site at pangenome.de
manuscript on bioRxiv