Virus evolution and population genetics
Richard Neher
Biozentrum, University of Basel
Viruses
 tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
bacteria phage (adenosine, wikipedia)
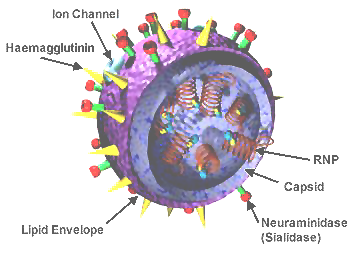
influenza virus wikipedia
human immunodeficiency virus wikipedia
- rely on host to replicate
- little more than genome + capsid
- genomes typically 5-200k bases (+exceptions)
- most abundant organisms on earth $\sim 10^{31}$
Evolution of HIV
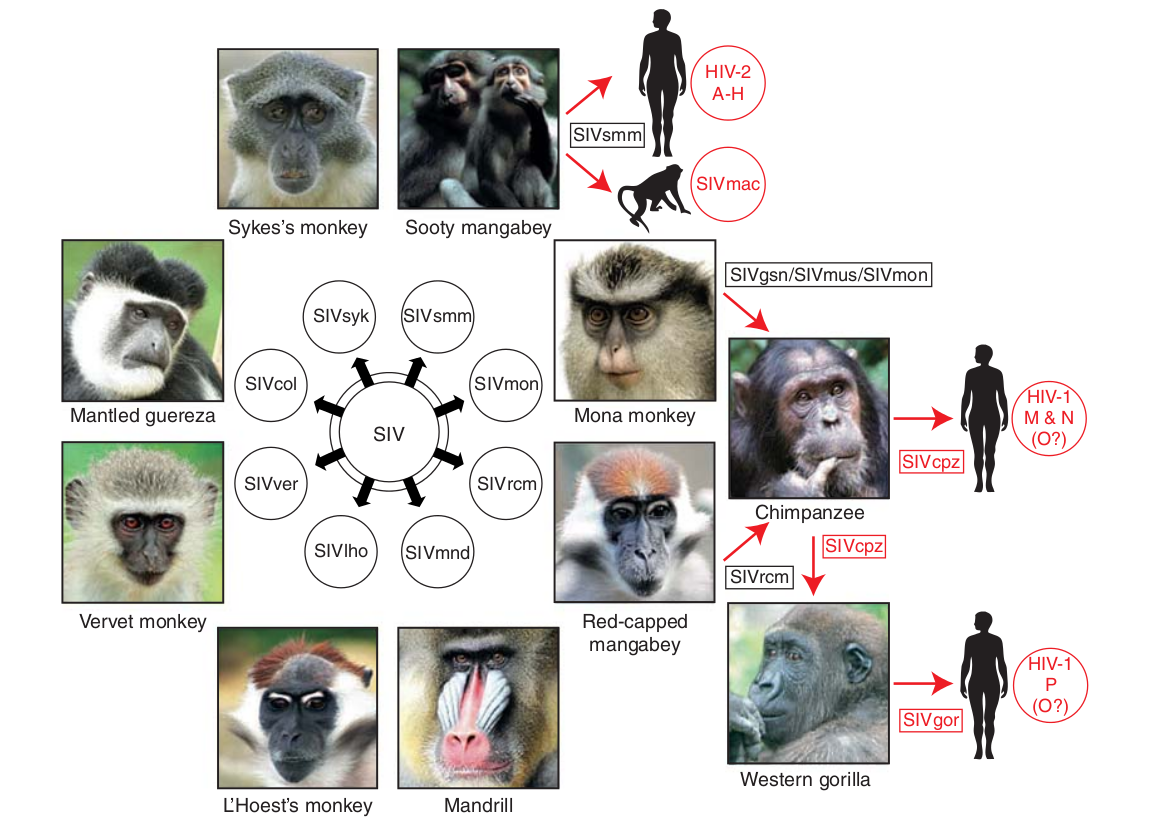
- Chimp → human transmission around 1900 gave rise to HIV-1 group M
- ~100 million infected people since
- subtypes differ at 10-20% of their genome
- HIV-1 evolves ~0.1% per year
HIV infection
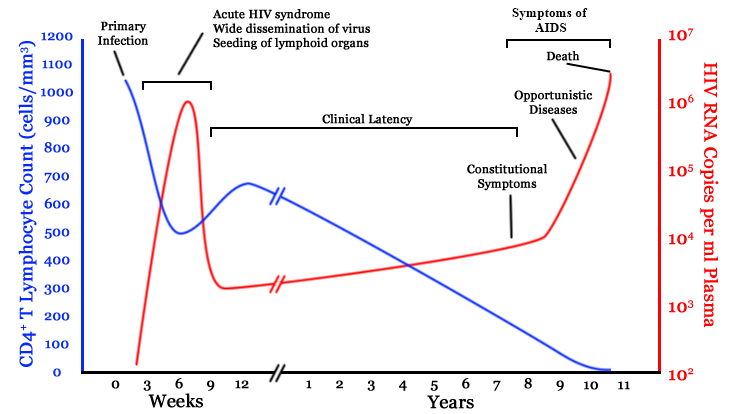
- $10^8$ cells are infected every day
- the virus repeatedly escapes immune recognition
- integrates into T-cells as
latent provirus
Some viruses evolve a million times faster than animals
Animal haemoglobin

HIV protein

Development of sequencing technologies
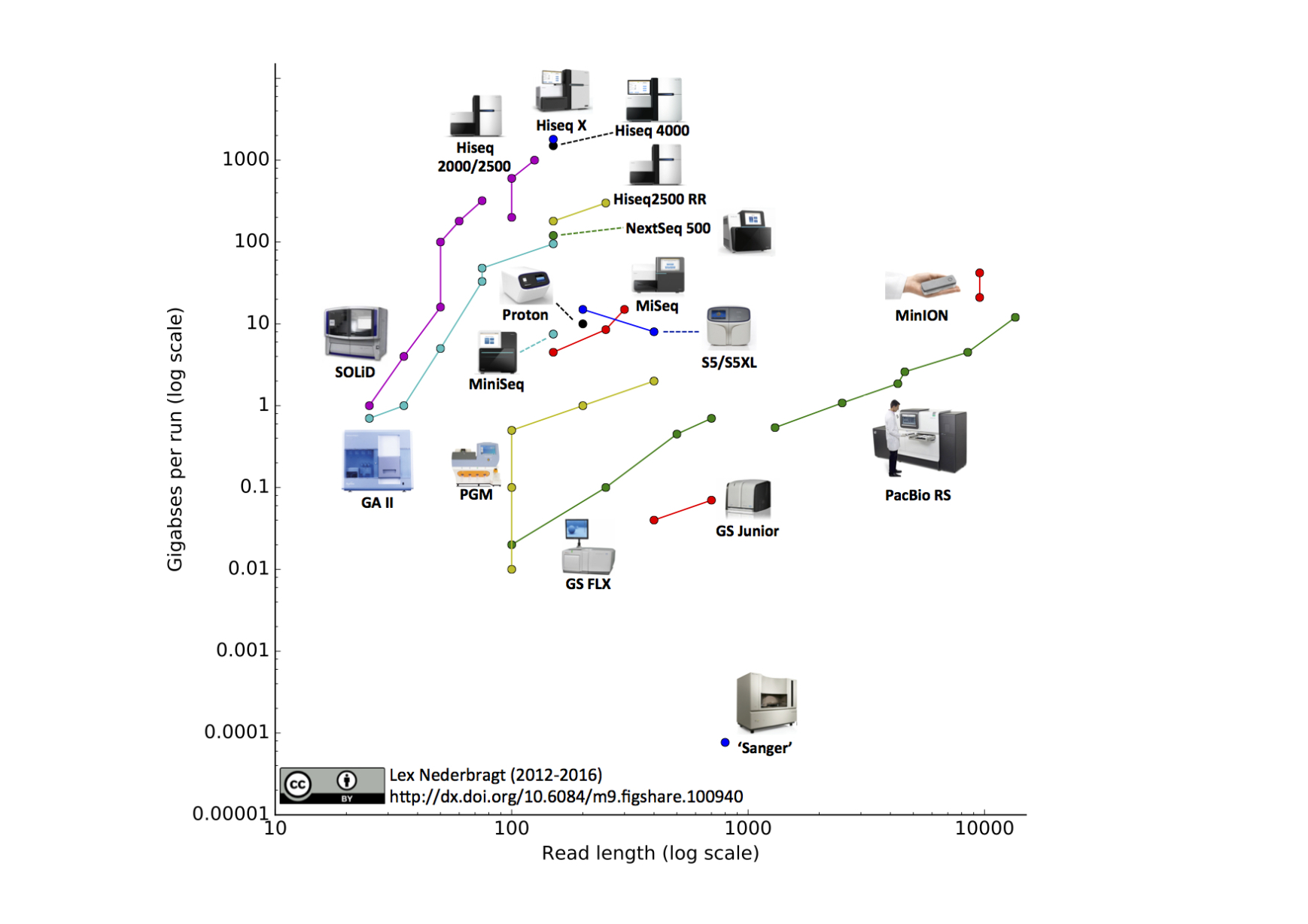
We can now sequence...
- thousands of bacterial isolates
- thousands of single cells
- populations of viruses, bacteria or flies
- diverse ecosystems
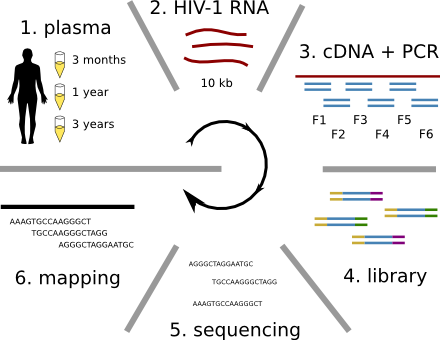
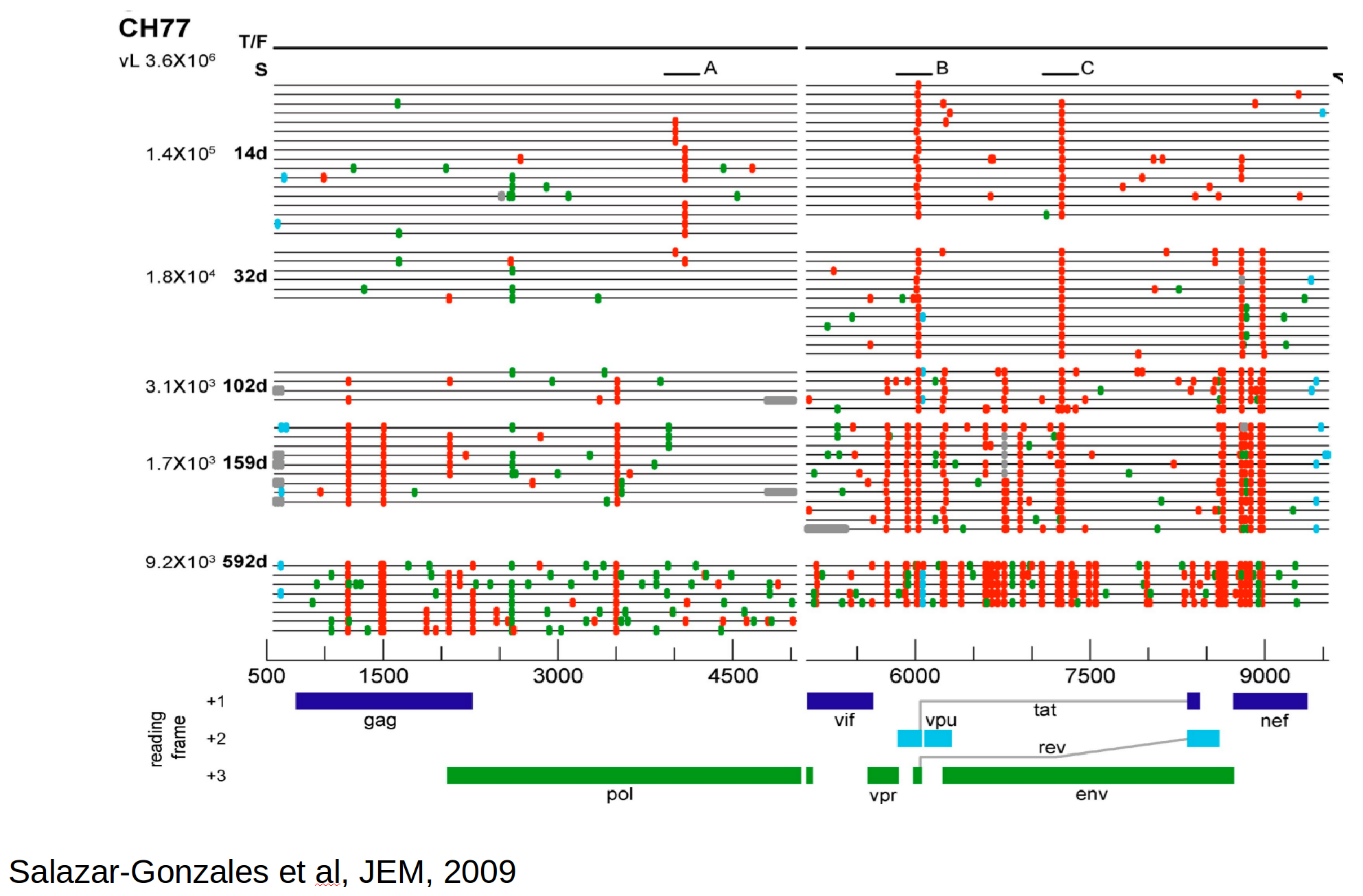
HIV-1 evolution within one individual

Immune escape in early HIV infection
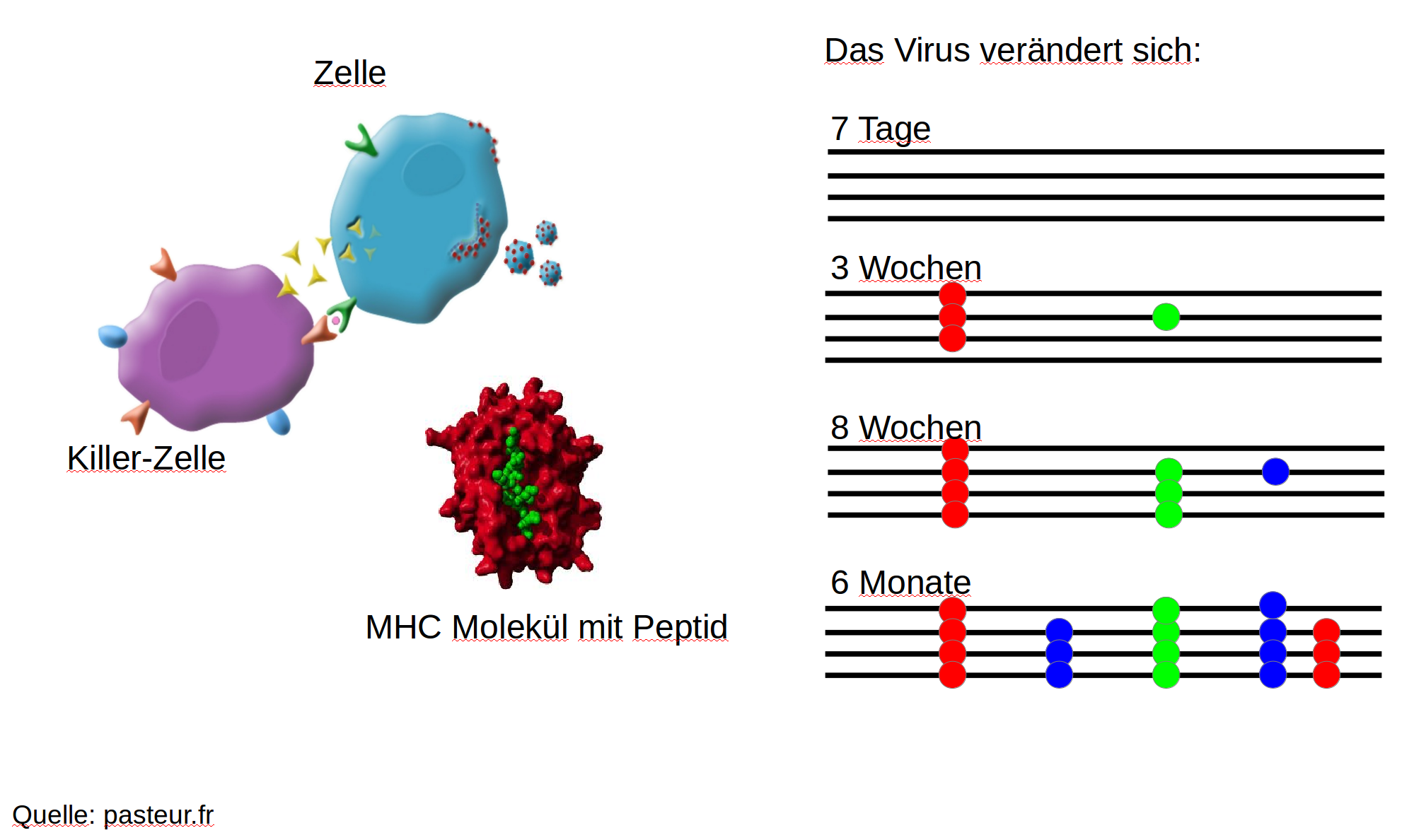
Immune escape in early HIV infection
Population genetics & evolutionary dynamics
evolutionary processes ↔ trees ↔ genetic diversity
Selective sweeps
- Viruses carrying a beneficial mutation have more offspring: on average $1+s$ instead of $1$
- $s$ is called selection coefficient
- Fraction $x$ of viruses carrying the mutation changes as $$x(t+1) = \frac{(1+s)x(t)}{(1+s)x(t) + (1-x(t))}$$
- In continuous time → logistic differential equation: $$\frac{dx}{dt} = sx(1-x) \Rightarrow x(t) = \frac{e^{s(t-t_0)}}{1+ e^{s(t-t_0)}}$$
Mutation rates and diversity and neutral sites
Balance between mutation and deleterious mutations
- mutation away from preferred state with rate $\mu$
- selection against non-preferred state with strength $s$
- variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
- equilibrium frequency: $\bar{x} = \mu/s $
- fitness cost: $s = \mu/\bar{x}$
Time-scaled phylogenies
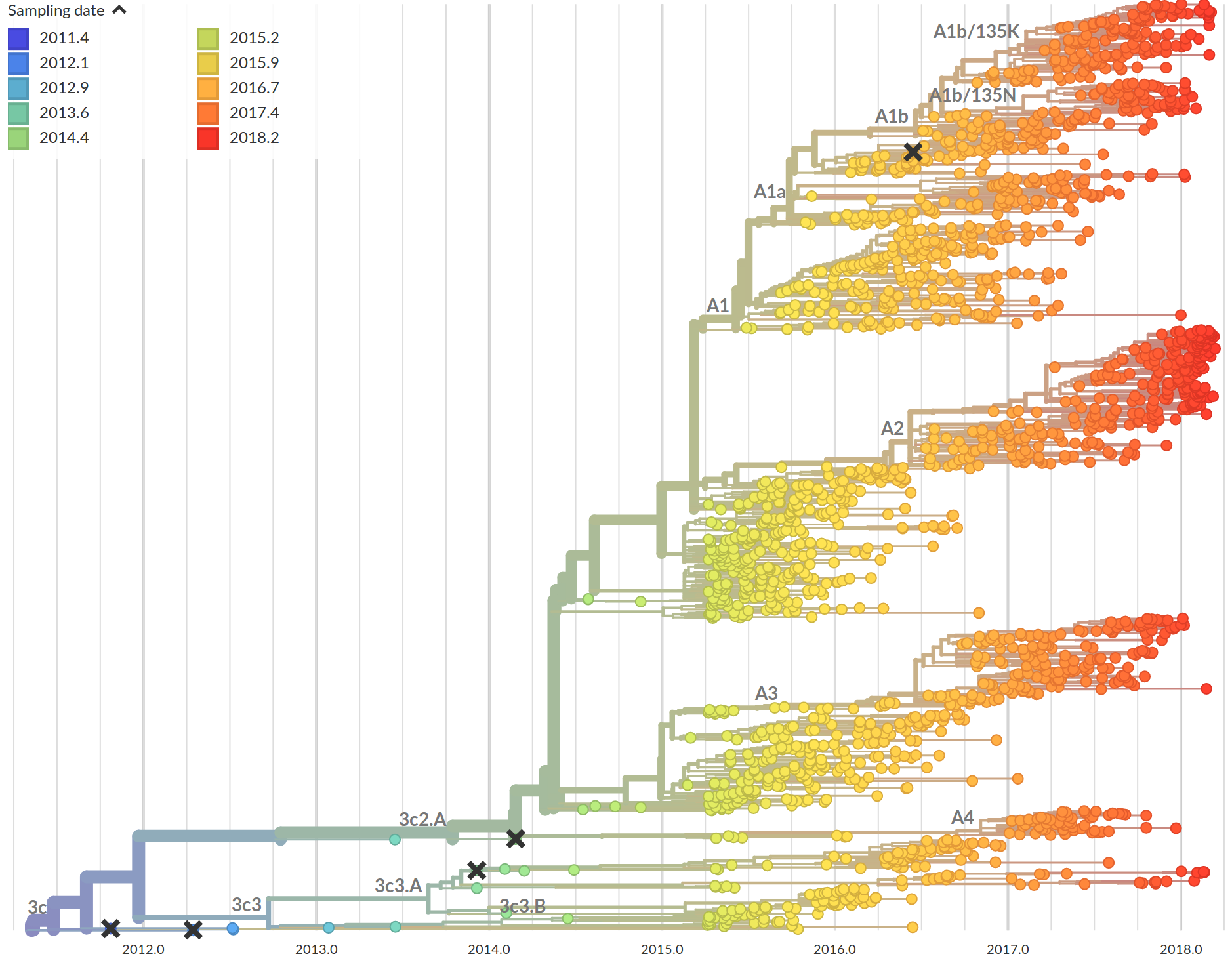
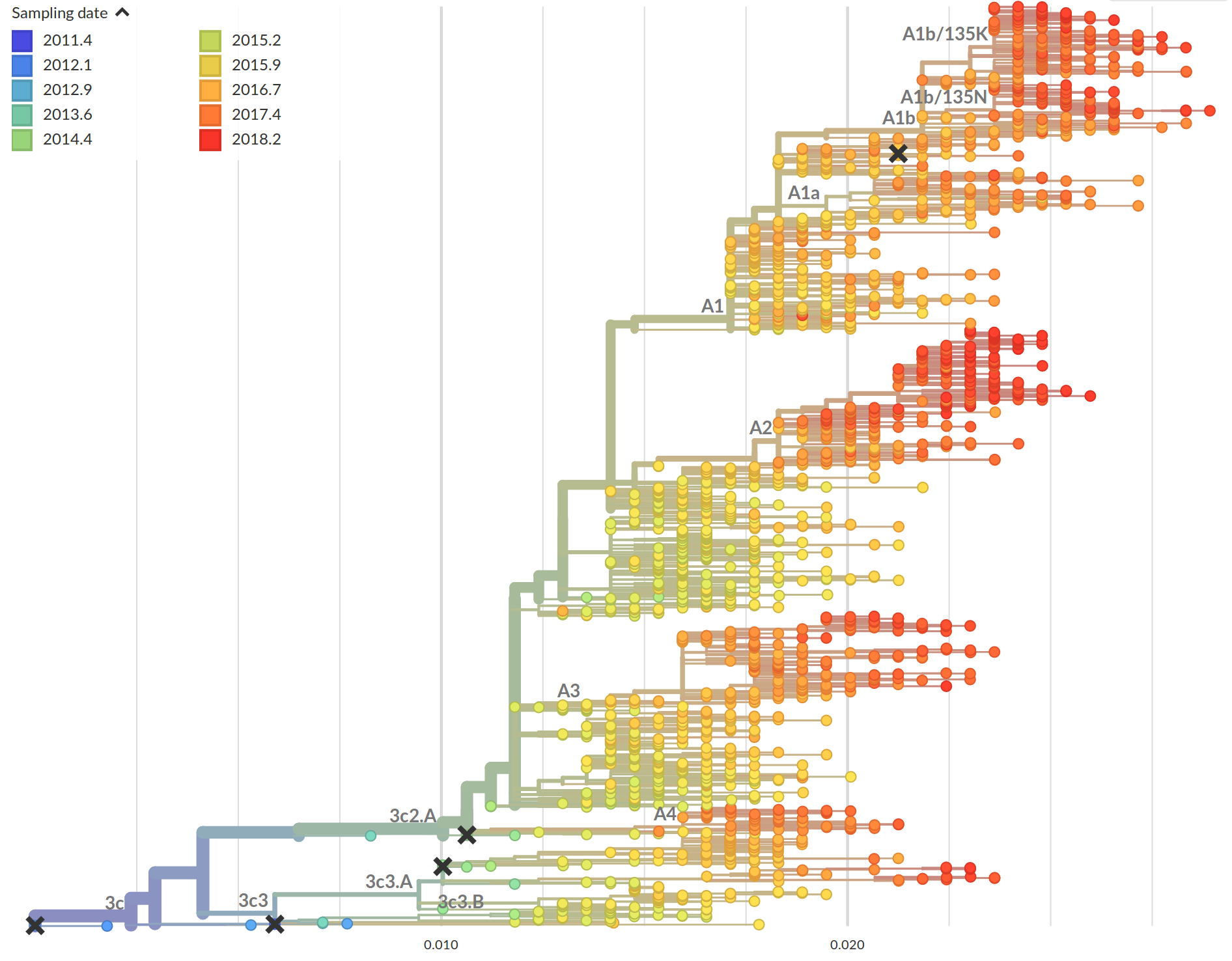
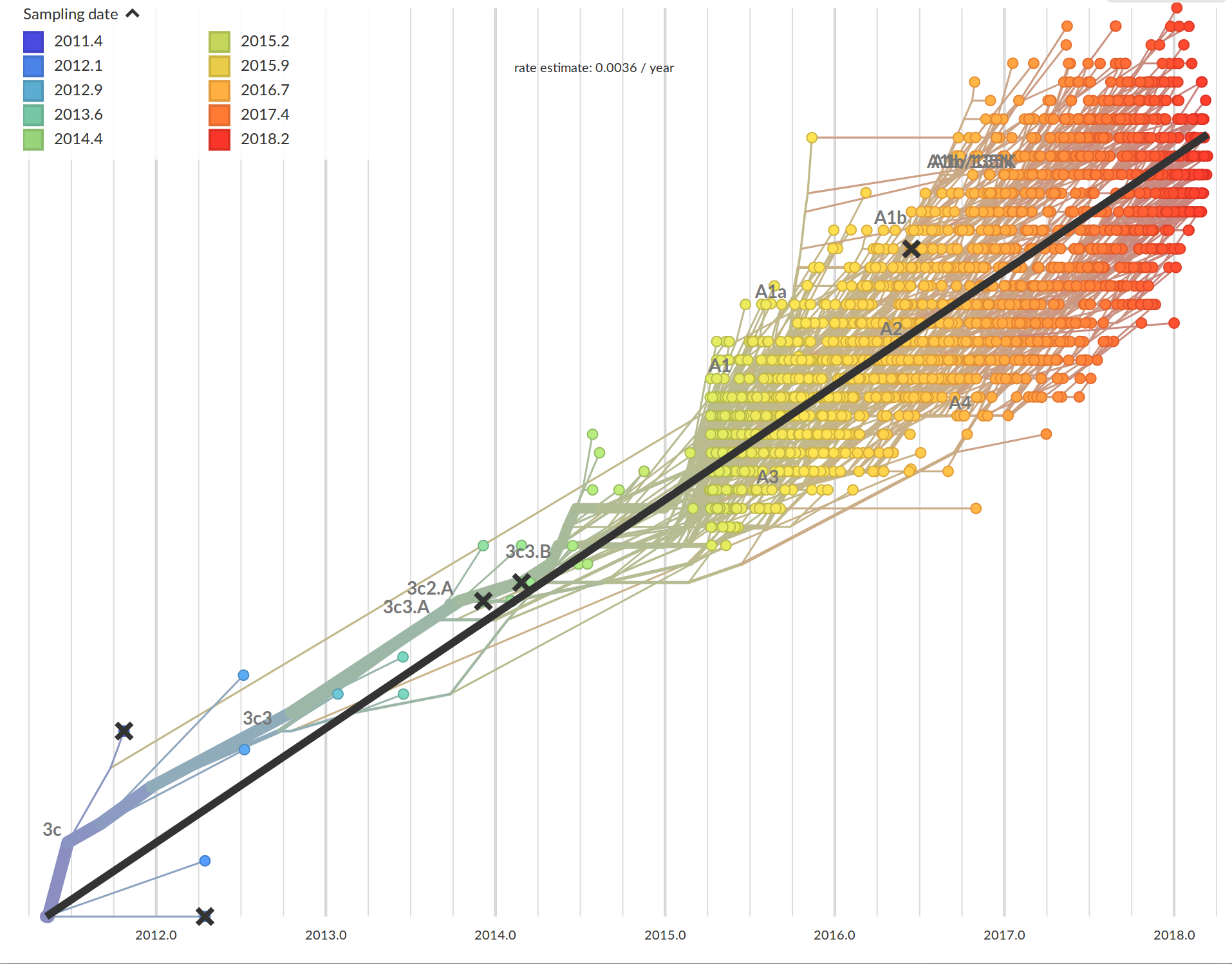
Tree building optimization with temporal constraints
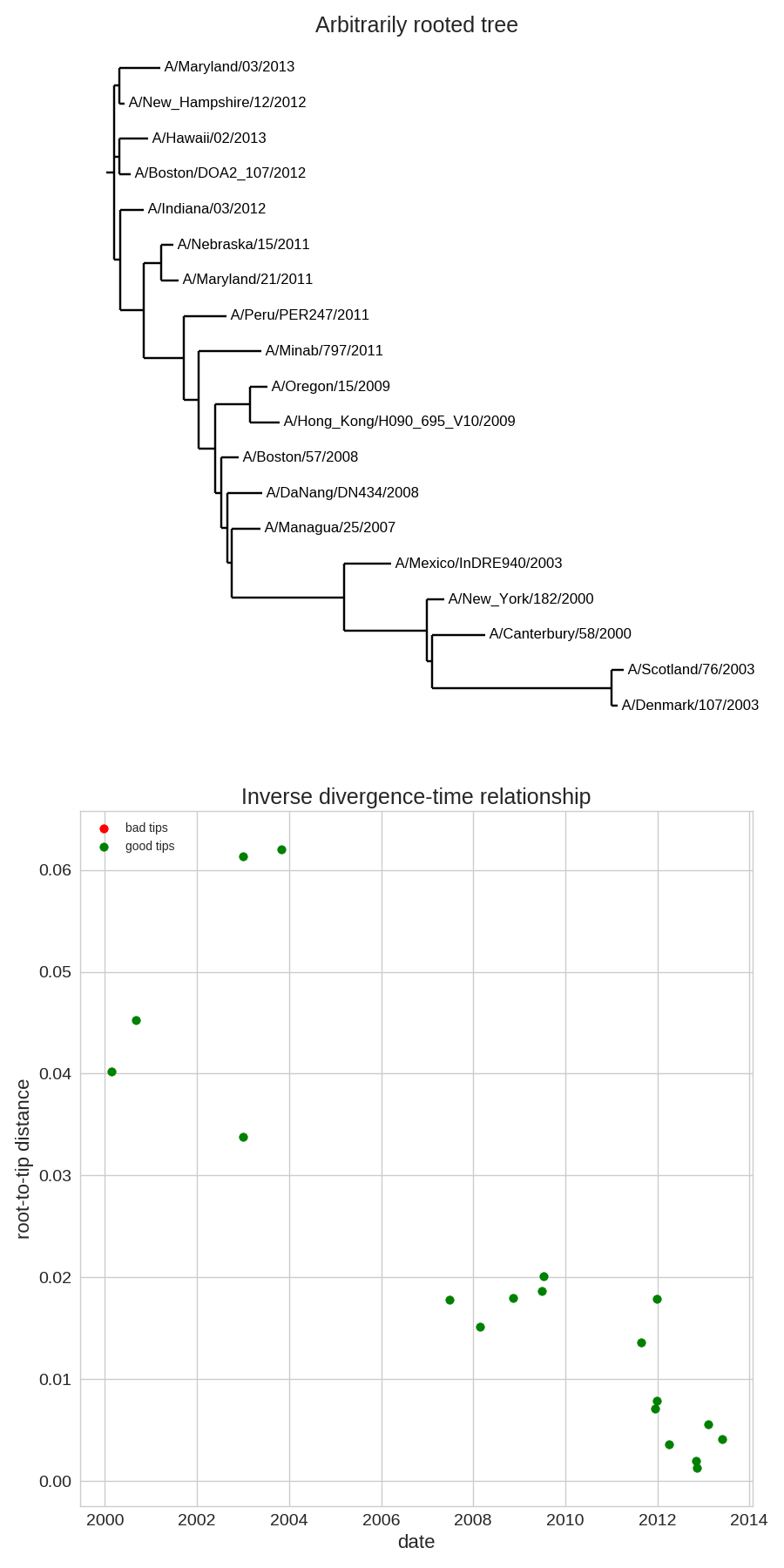
- Time stamps single out a root
- Root can be found by optimizing root-to-tip regression
- BEAST: Markov-Chain Monte Carlo tree sampler
- If topology is correct, temporal constraints can be accounted for in linear time
- Multiple tools: treedate, LSD, treetime
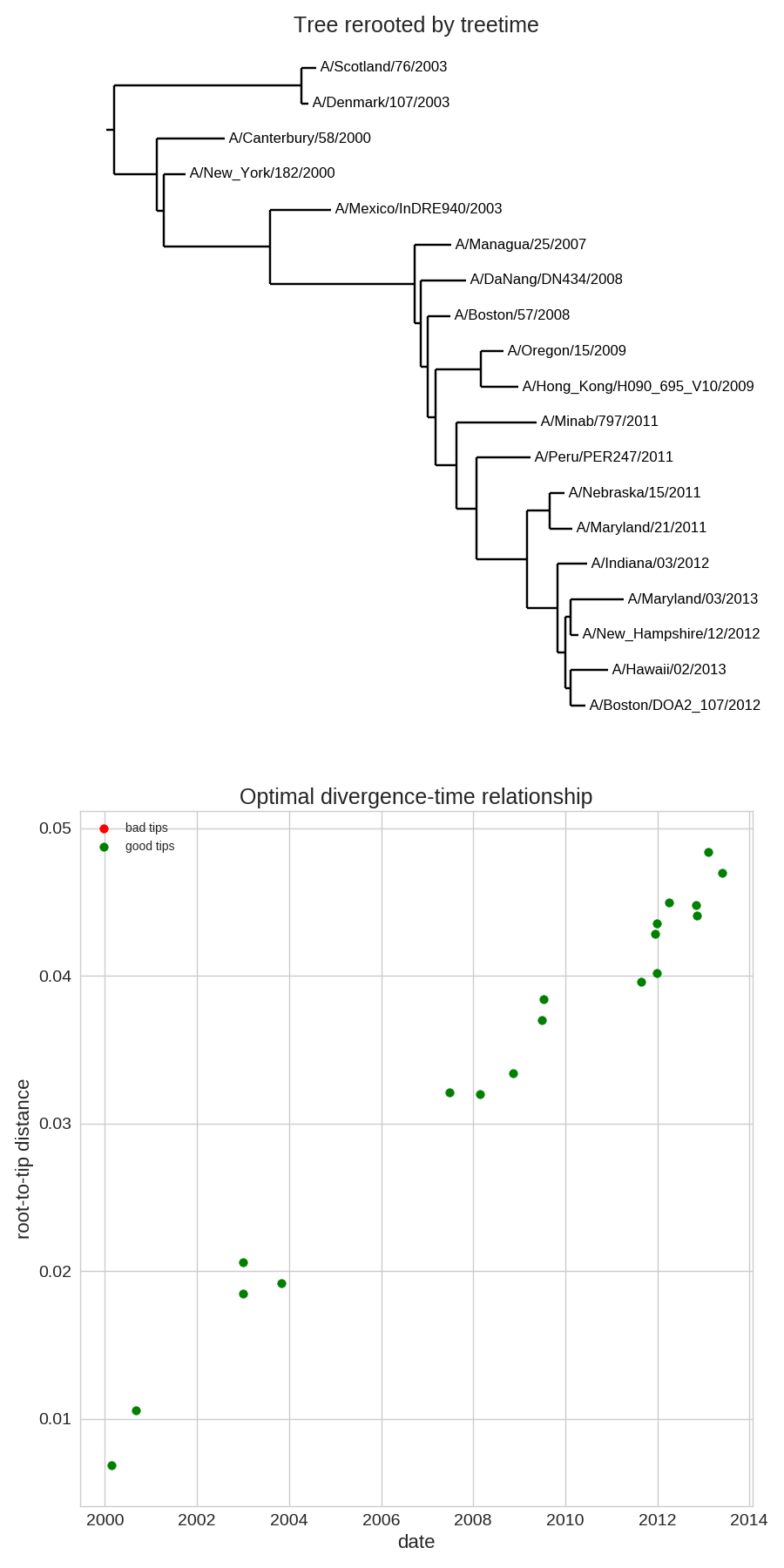
Time-scaled phylogenies

Attach sequences and dates

Propagate temporal constraints via convolutions

Integrate up-stream and down-stream constraints
Time-scaled phylogenies
- Calibration points can be longitudinal samples, ancient DNA or fossils
- Rates can vary between proteins and organisms from 0.01/year to $<10^{-8}$/y
- Some site change often, some rarely → saturation
- The apparent rate changes over time
- Divergence times are often under estimated.