Real-time phylodynamics with nextflu and nextstrain


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/201806_BSSE.html

How this all started...

.... population genetics of rapid adaptation and predicting flu

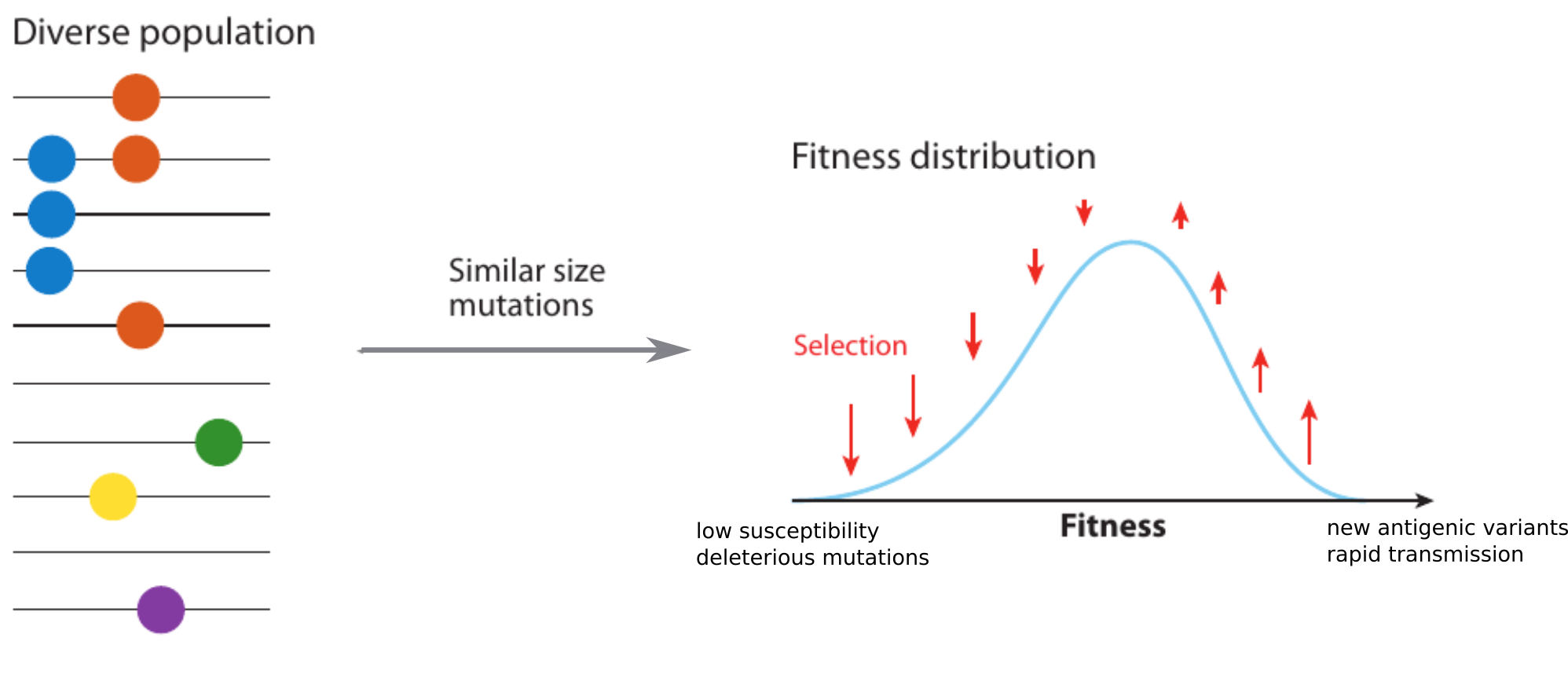
Model of rapidly adapting virus populations

RN, Annual Reviews, 2013; Desai & Fisher; Brunet & Derrida; Kessler & Levine

Typical tree

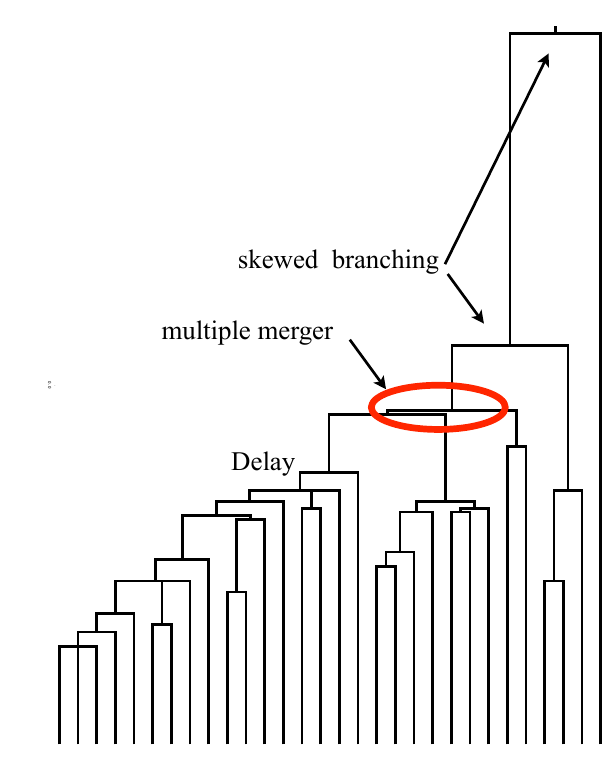
Bolthausen-Sznitman Coalescent

RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007; Desai, Walczak, Fisher, Genetics, 2013

Bursts in a tree ↔ high fitness genotypes

Predicting evolution

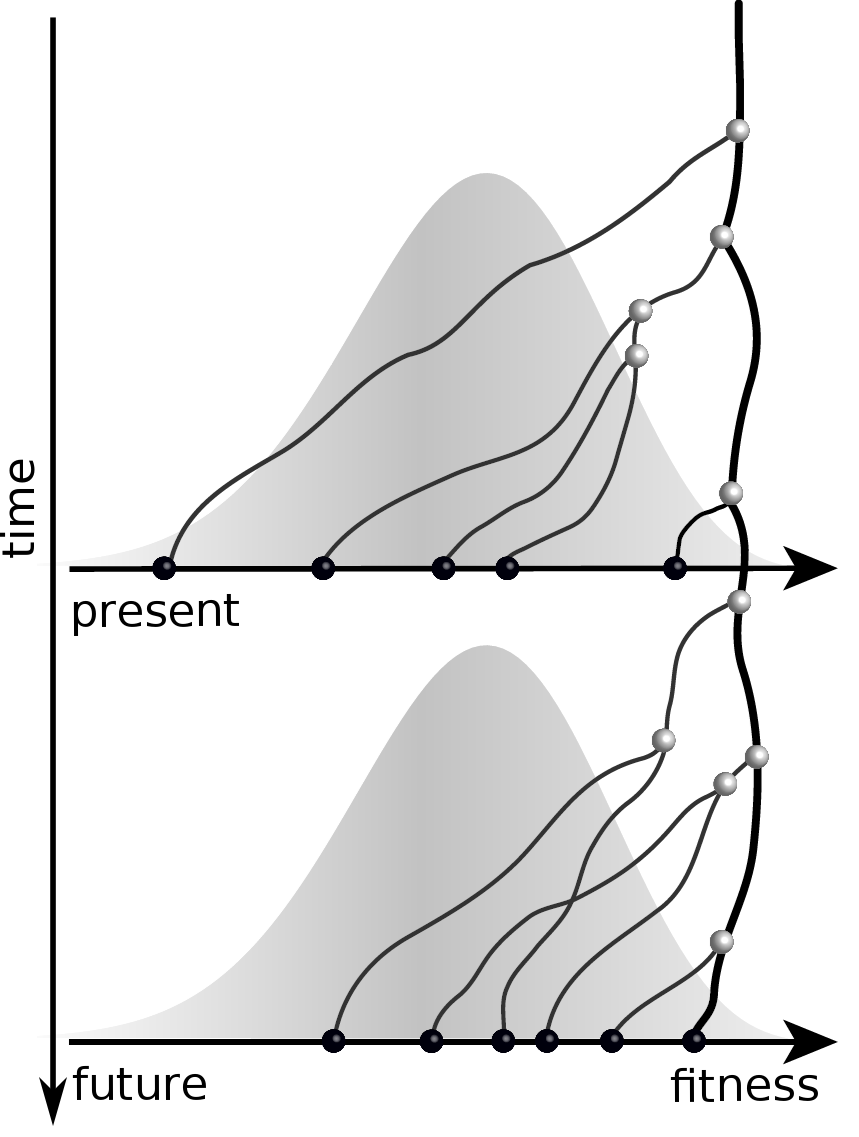
Given the branching pattern:

  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$ $$\partial_t g( x,t'|y, t) = [y - 2\phi_{\omega} (y,t)] g(x,t'| y,t)-\sigma^2 \partial_yg( x,t'| y, t) +D \partial_y^2 g( x,t'|y,t)$$
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

nextstrain.org/flu

joint work with Trevor Bedford & his lab

code at github.com/nextstrain

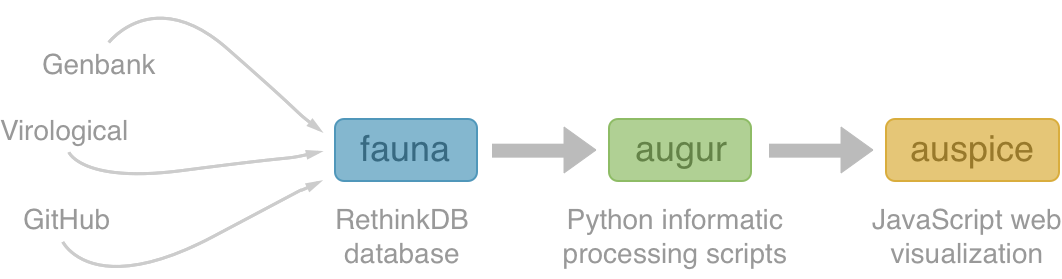
NextStrain architecture

Using treetime to rapidly compute timetrees

TreeTime: maximum likelihood phylodynamic analysis

desired features:
  • ancestral sequences
  • divergence times
  • ancestral geographic distribution
  • population dynamics
Typical approach: Bayesian parameter estimation
  • flexible
  • probabilistic → confidence intervals etc
  • but: computationally expensive
TreeTime by Pavel Sagulenko
  • probabilistic treatment of divergence times
  • dates trees with thousand sequences in a few minutes
  • linear time complexity
  • fixed tree topology
  • github.com/neherlab/treetime
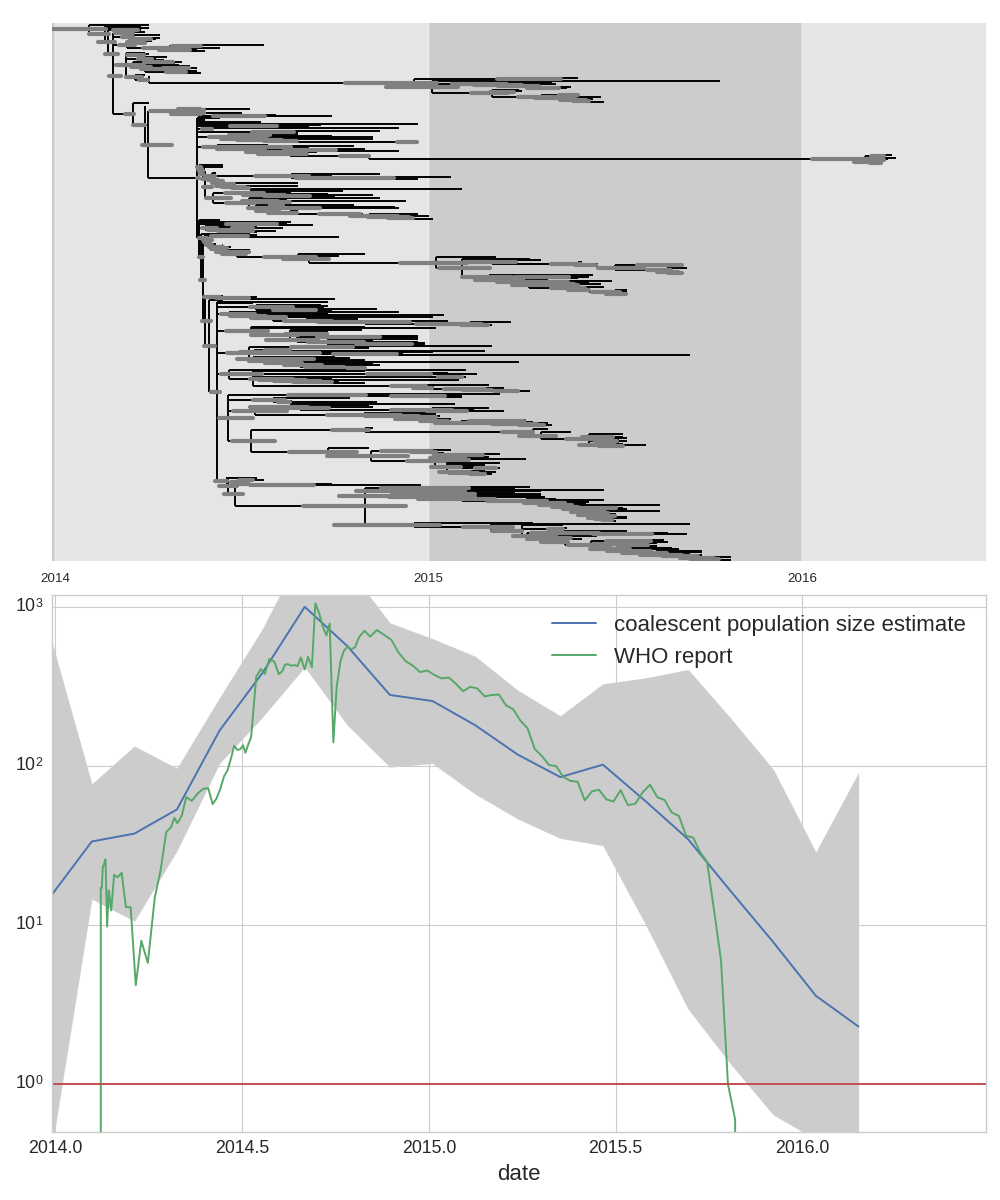
West African Ebola virus outbreak

TreeTime: nuts and bolts

Attach sequences and dates
Reconstruct ancestral sequences
Propagate temporal constraints via convolutions
Integrate up-stream and down-stream constraints
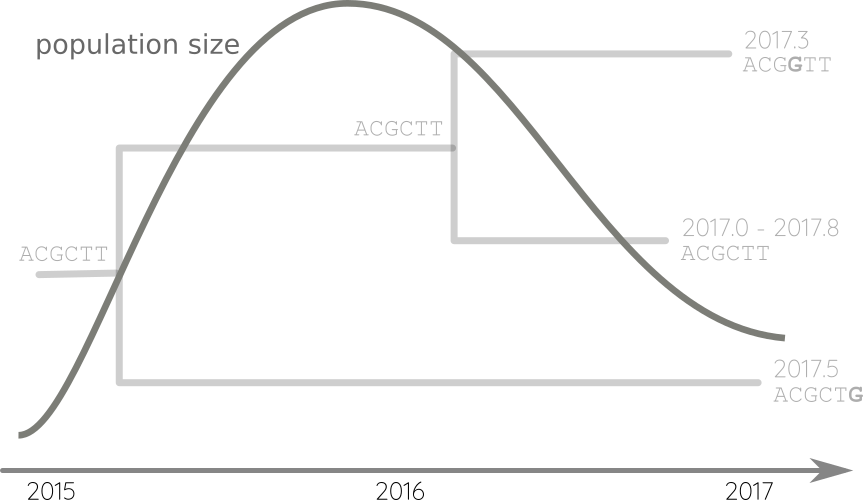
Fit phylodynamic model → iterate

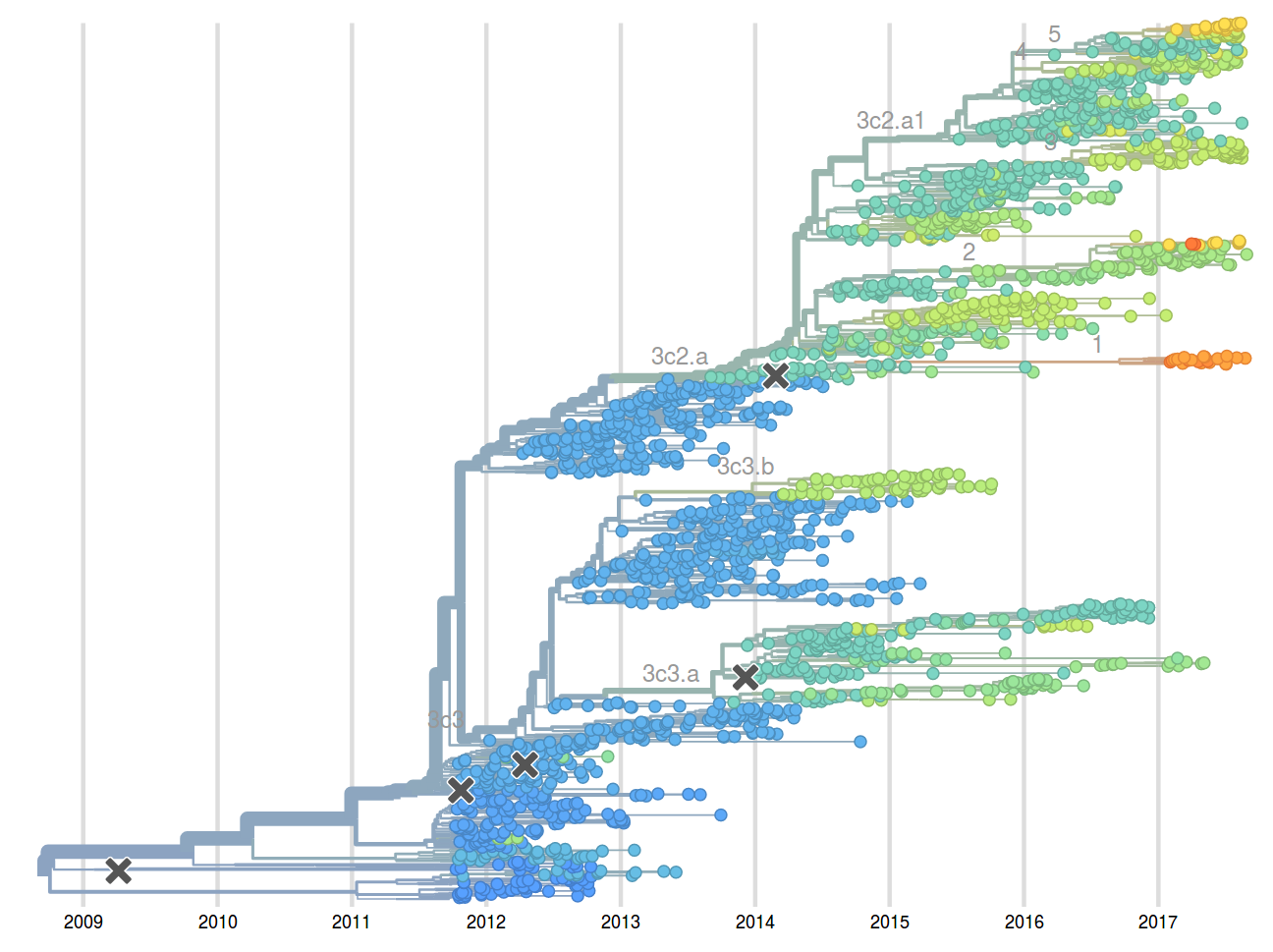
Molecular clock phylogenies of ~2000 A/H3N2 HA sequences -- a few minutes

Integrating phenotype and genotype data

Slide by Trevor Bedford

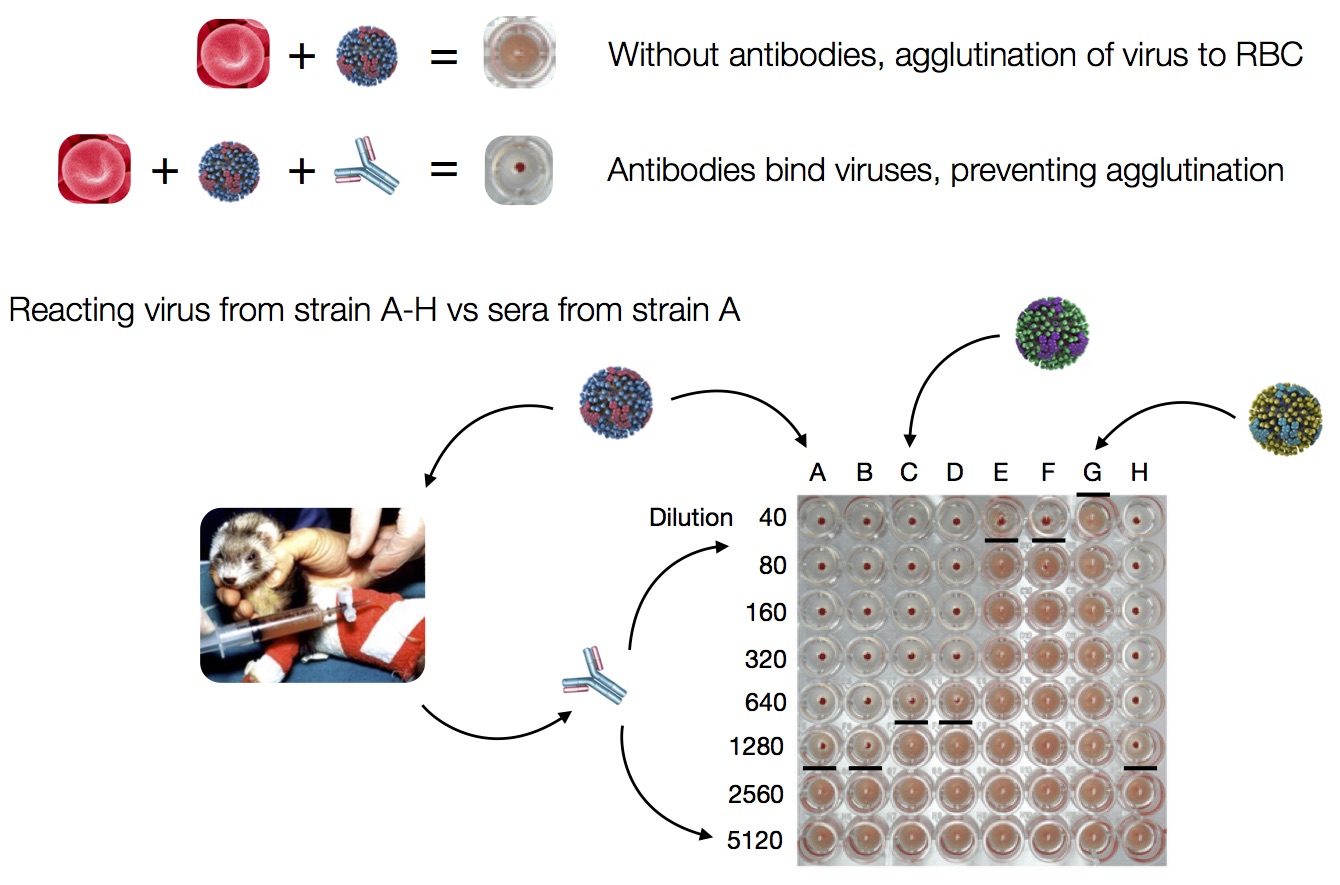
Antigenic distance tables

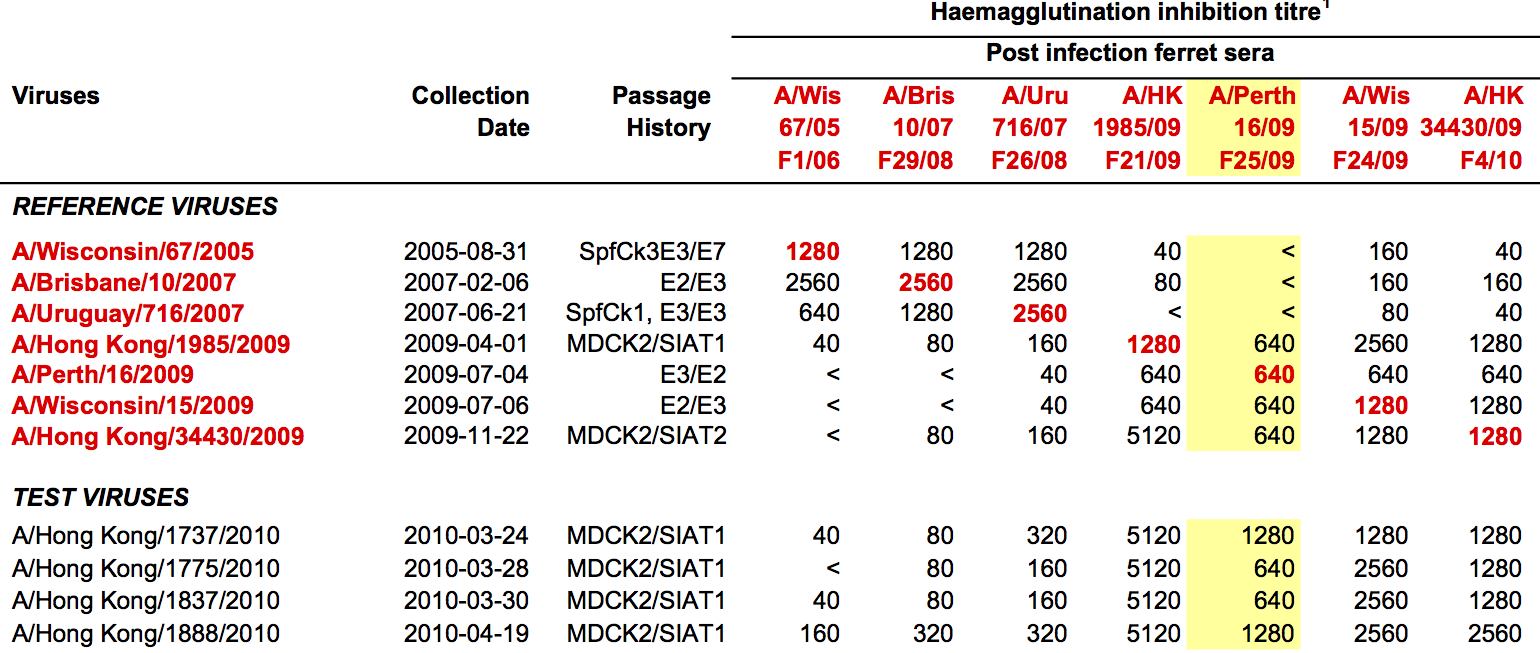
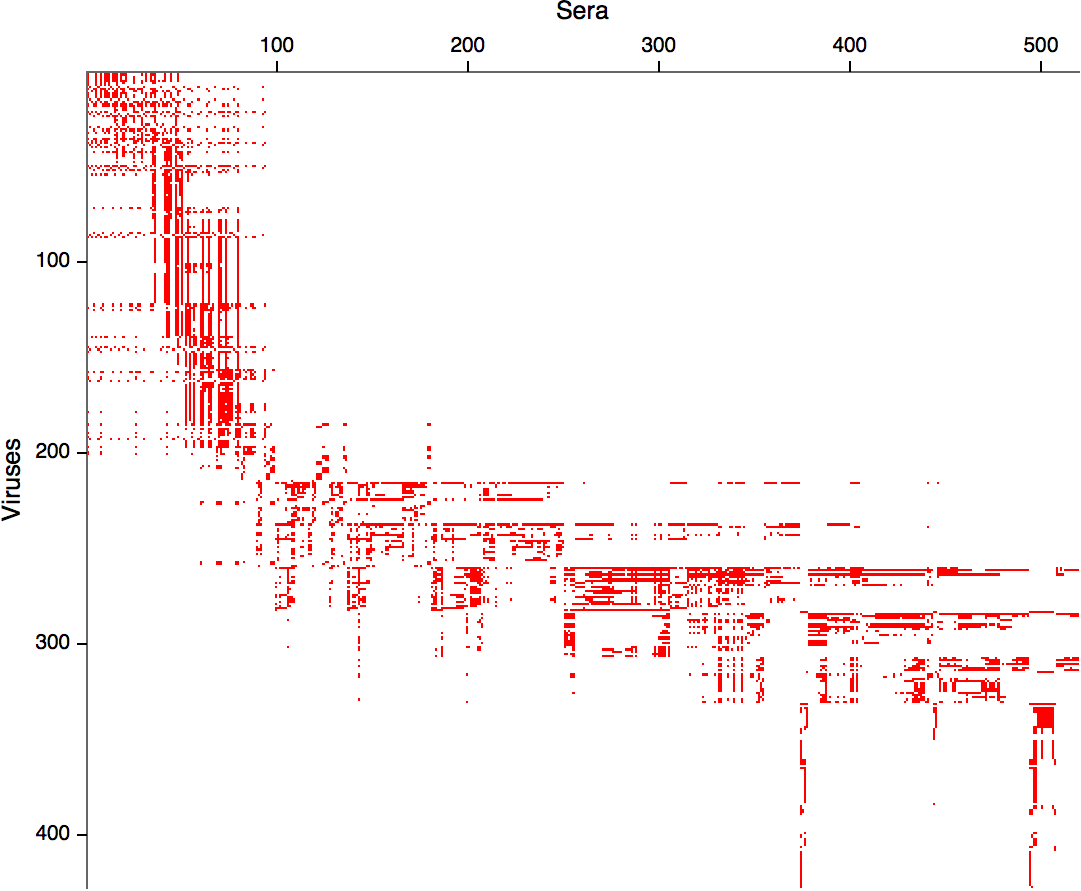
  • Long list of distances between sera and viruses
  • Tables are sparse, only close by pairs
  • Structure of space is not immediately clear
  • MDS in 2 or 3 dimensions
Slide by Trevor Bedford

Integrating antigenic and molecular evolution

  • each branch contributes $d_i$ to antigenic distance
  • sparse solution for $d_i$ through $l_1$ regularization
RN et al, PNAS, 2016

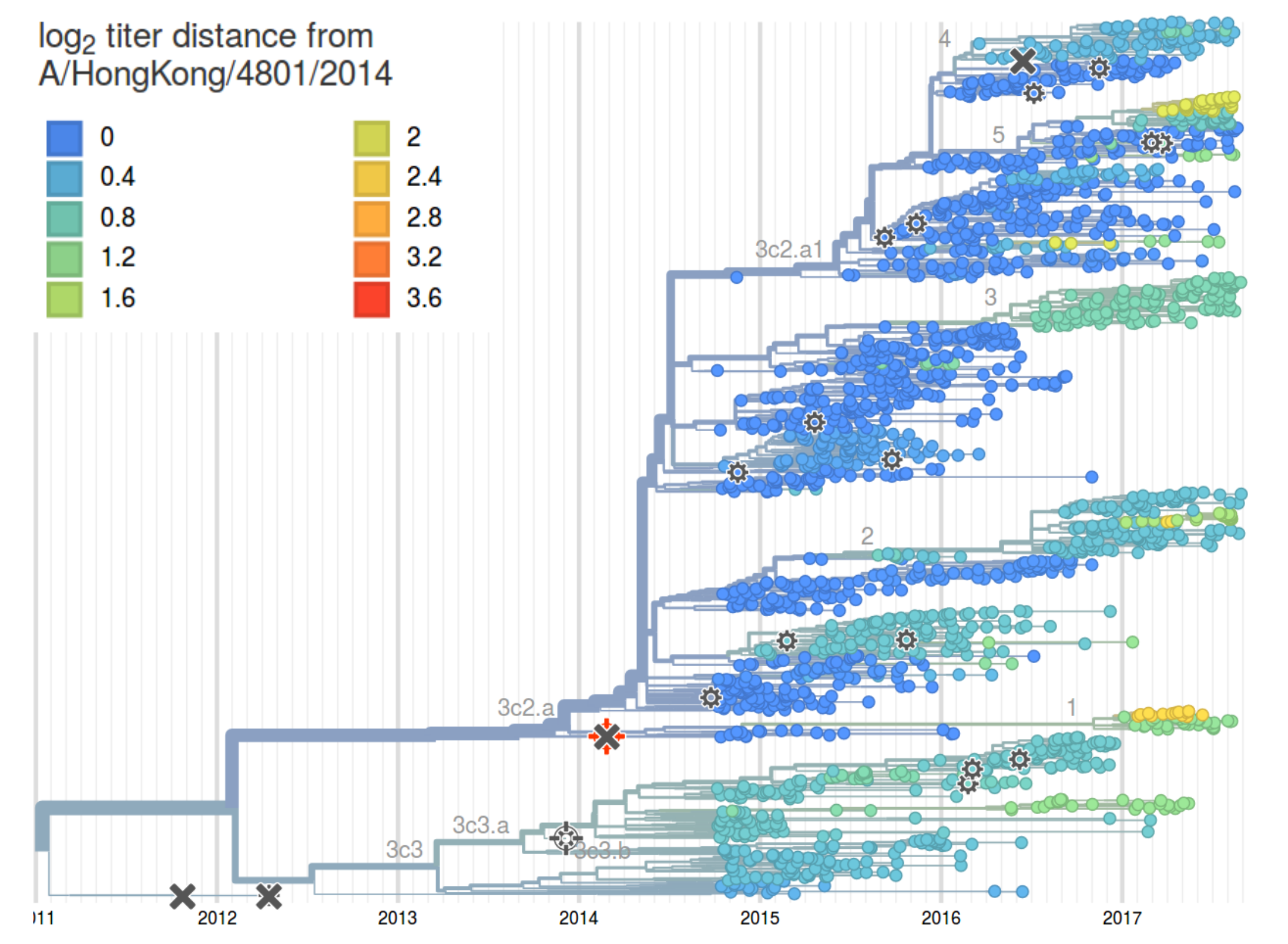
HI distances on the phylogenetic tree

Acknowlegdements

  • Trevor Bedford
  • Colin Megill
  • Pavel Sagulenko
  • Sidney Bell
  • James Hadfield
  • Wei Ding
  • Emma Hodcroft
  • Sanda Dejanic