Universality and predictability in RNA virus evolution


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/201810_cuny.html

Human seasonal influenza viruses

slide by Trevor Bedford


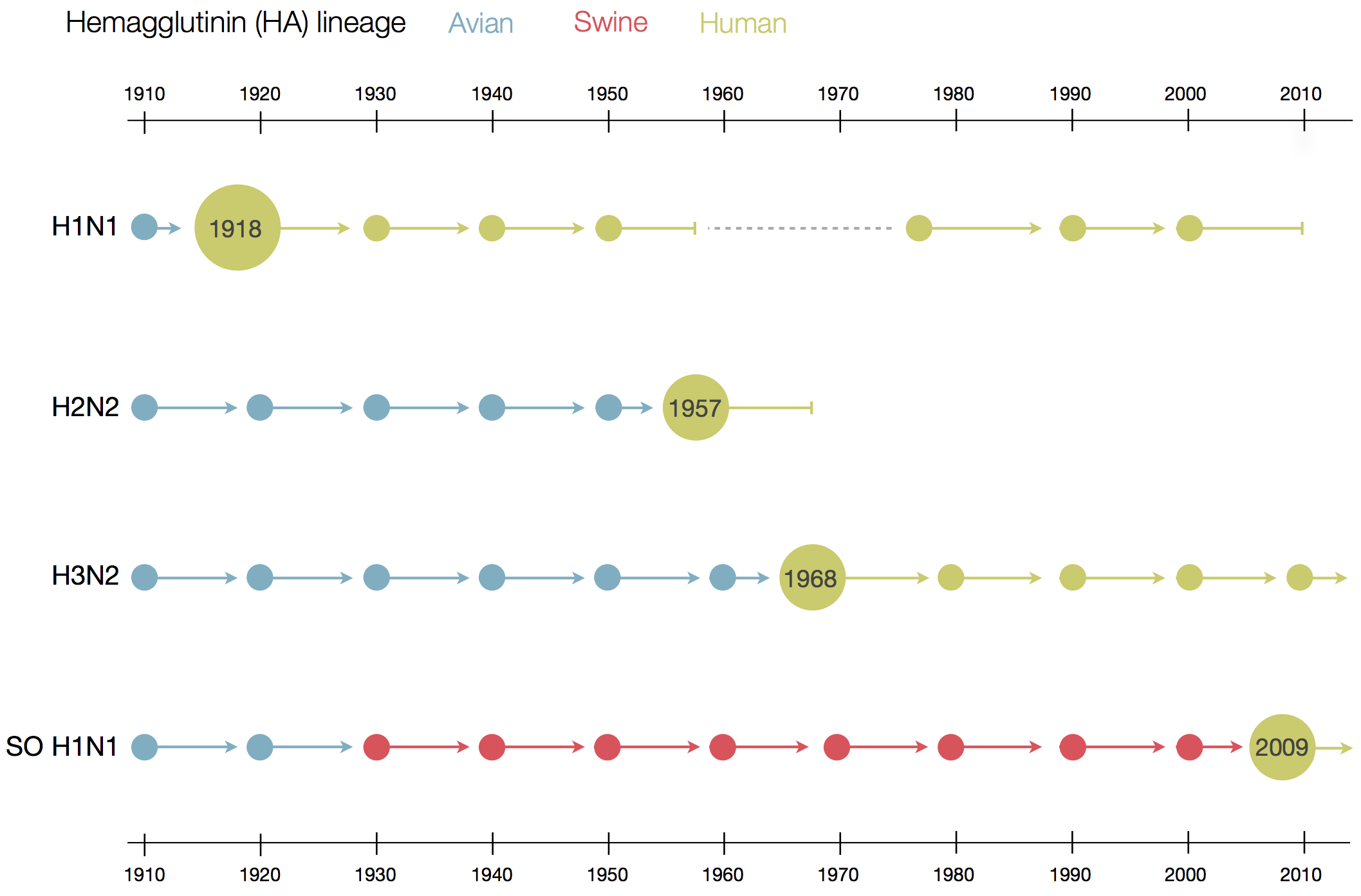
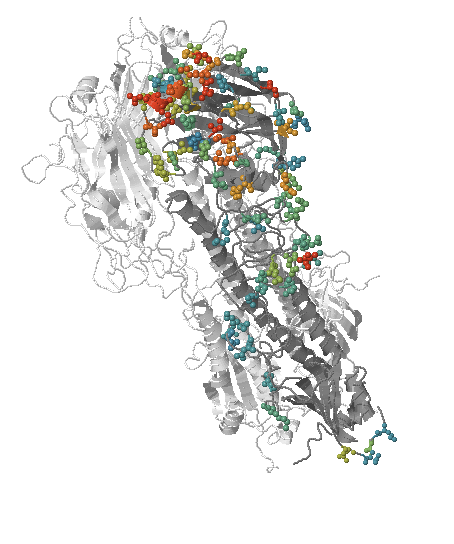
  • Influenza virus evolves to avoid human immunity
  • Vaccines need frequent updates

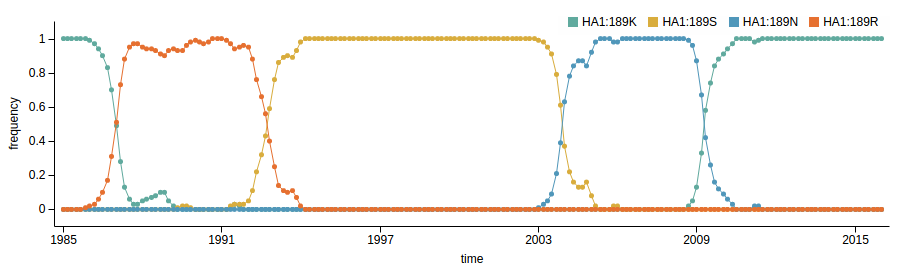
Virus evolution happens within hosts!

This is much easier to study in HIV than influenza

HIV infection

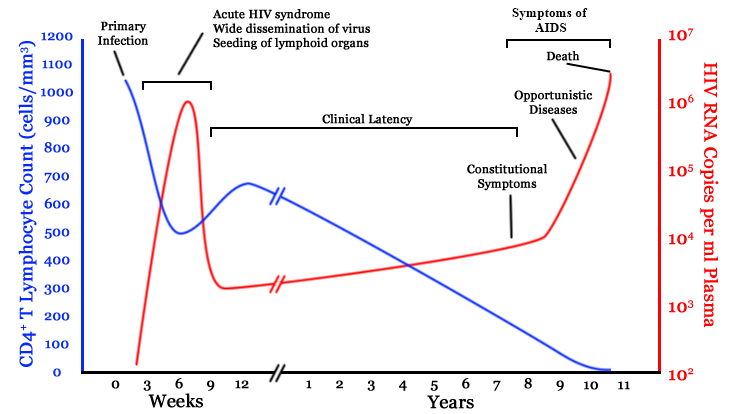
  • $10^8$ cells are infected every day
  • the virus repeatedly escapes immune recognition
  • integrates into T-cells as latent provirus
image: wikipedia

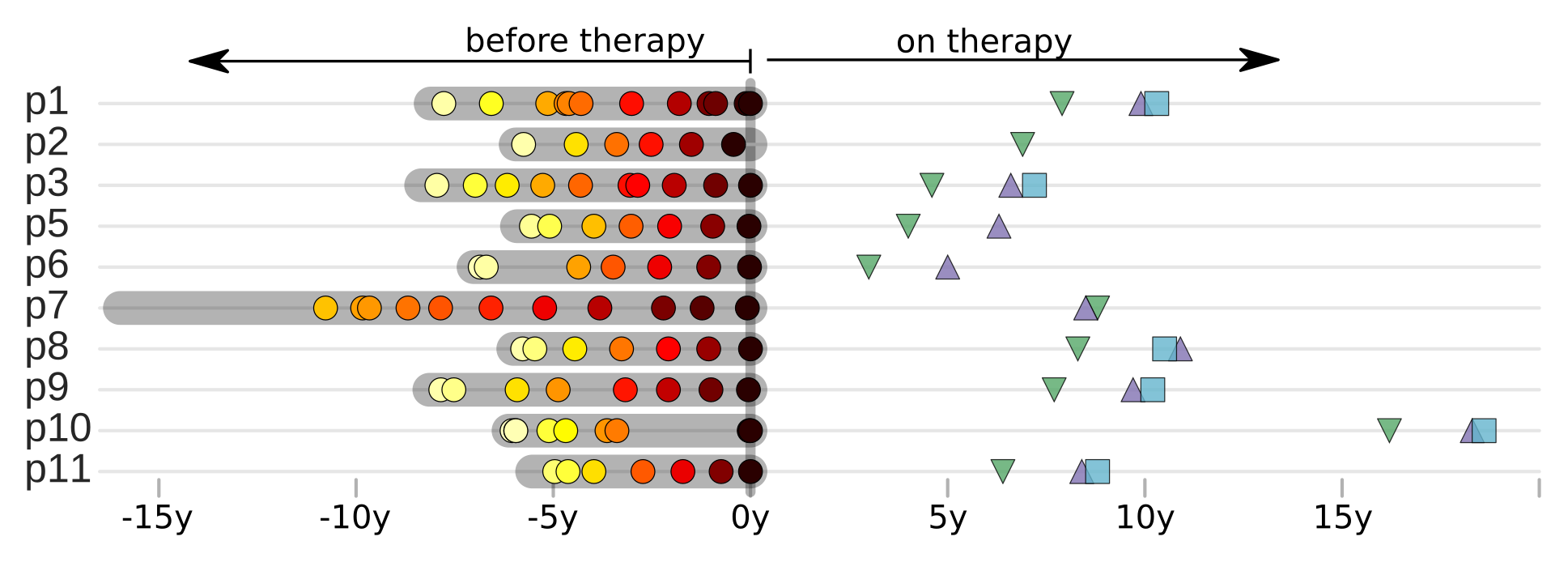
HIV-1 evolution within one individual



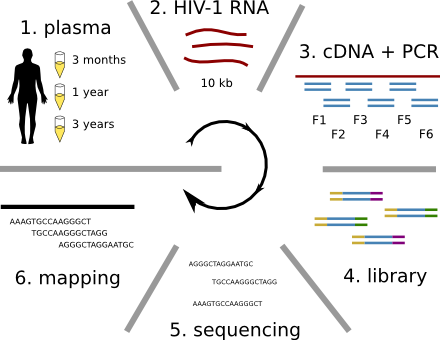
silouhette: clipartfest.com, Zanini at al, 2015. Collaboration with Jan Albert and his group

HIV-1 sequencing before and after therapy

Zanini et al, eLife, 2015; Brodin et al, eLife, 2016. Collaboration with the group of Jan Albert

Population sequencing to track all mutations above 1%

Zanini et al, eLife, 2015; antibody data from Richman et al, 2003

Approximately neutral divergence -- silent mutations

Zanini et al, Virus Evolution, 2017

In vivo mutation rate estimates

Zanini et al, Virus Evolution, 2017

Divergence at increasingly conserved positions

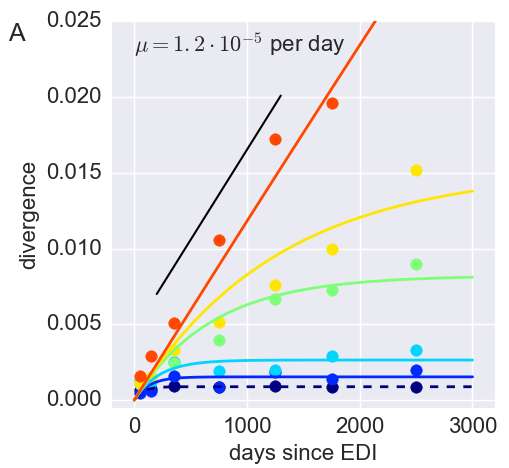
  • Six categories from high to low conservation
  • deleterious mutations arise with rate $\mu$
  • selection against them with strength $s$
  • variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
  • equilibrium frequency: $\bar{x} = \mu/s $
  • fitness cost: $s = \mu/\bar{x}$
  • Fit model of minor variation to categories of conservation
  • $\Rightarrow$ harmonic average fitness cost in category

Fitness landscape of HIV-1

Zanini et al, Virus Evolution, 2017

Selection on RNA structures and regulatory sites

  • Blue: all mutations
  • Red: only mutations that don't change amino acids
Zanini et al, Virus Evolution, 2017

Immune adaptation

Zanini et al, eLife, 2015

Theory, models...?

  • about 10-20 mutations fix in the HIV per year
  • many of them are beneficial
  • 100s of mutations at low frequencies
  • most of them compromise viral replication mildly

Fitness variation in rapidly adapting populations

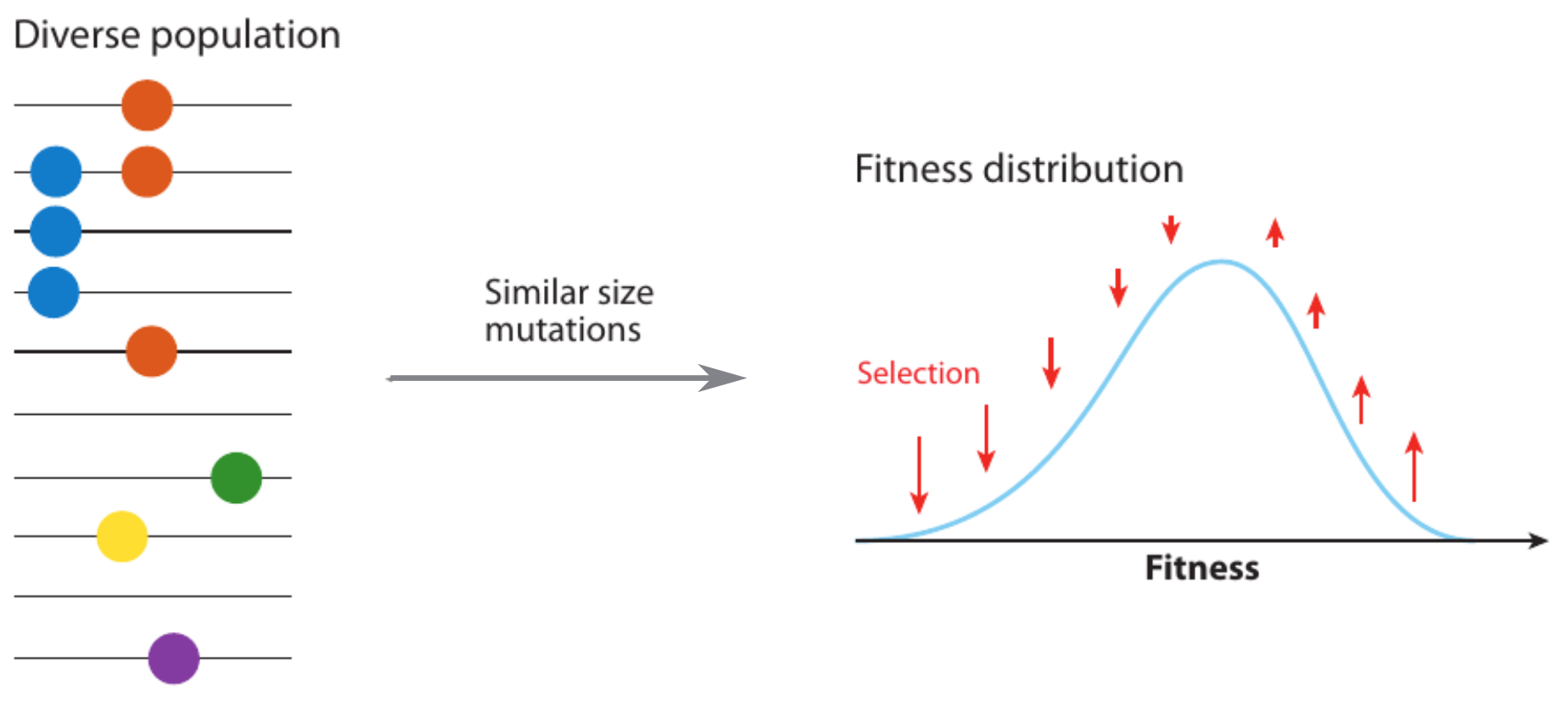
RN, Annual Reviews, 2013; Desai & Fisher; Brunet & Derride; Kessler & Levine

Traveling wave models of adaptation

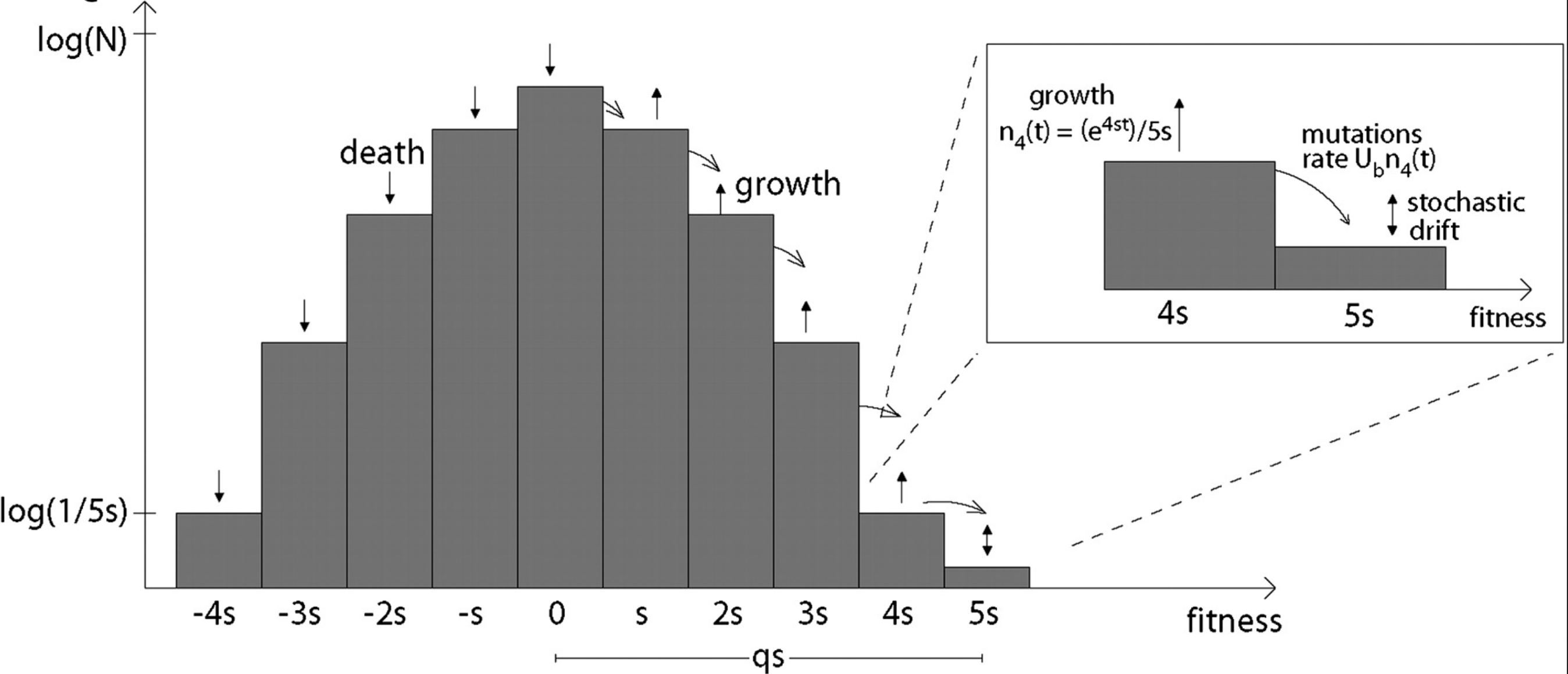
  • Speed of adaptation is logarithmic in population size
  • Environment (fitness landscape), not mutation supply, determines adaptation
  • Different models have universal emerging properties
Desai & Fisher, Genetics

Dynamics, genetic diversity, and phylogenetic trees

evolutionary processes ↔ trees ↔ genetic diversity

Neutral/Kingman coalescent

strong selection

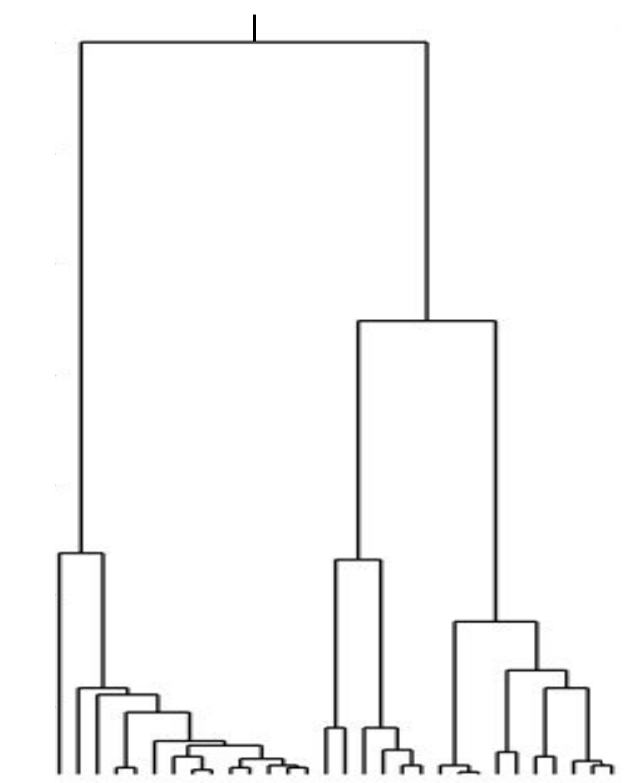
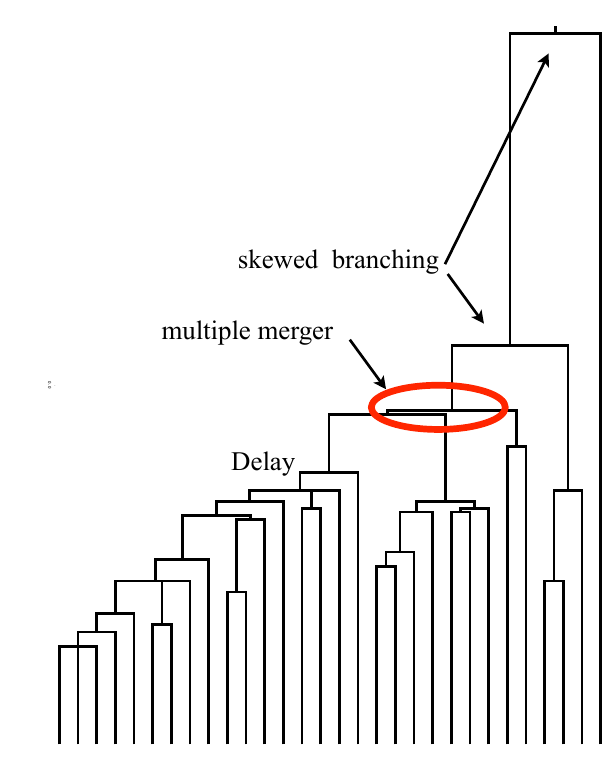
Bolthausen-Sznitman Coalescent

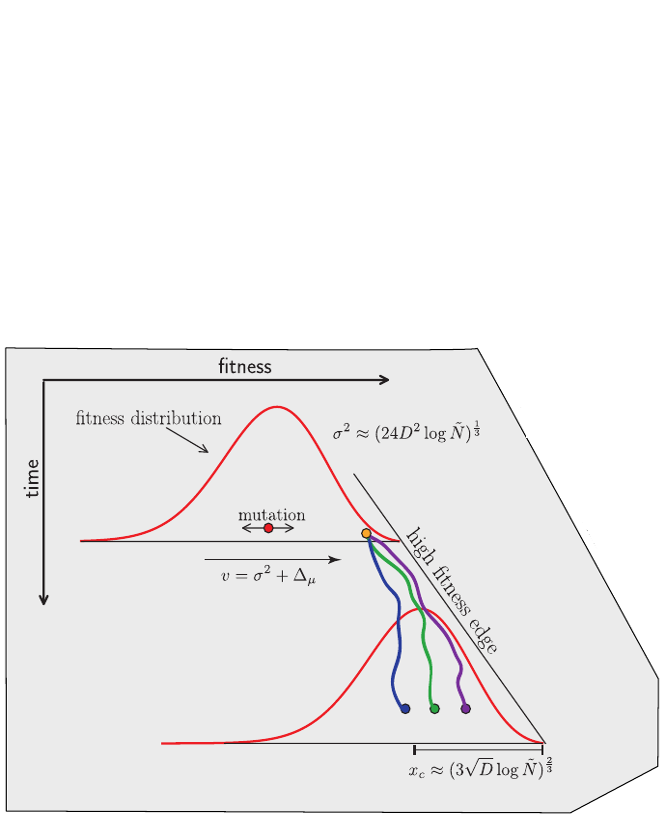
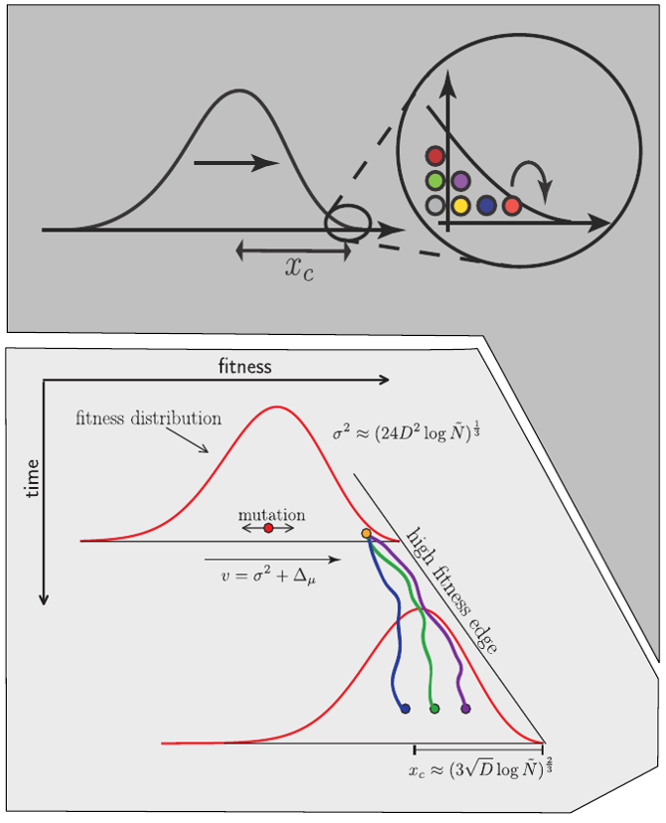
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007; Desai, Walczak, Fisher, Genetics, 2013

Traveling waves and the Bolthausen-Snitman coalescent

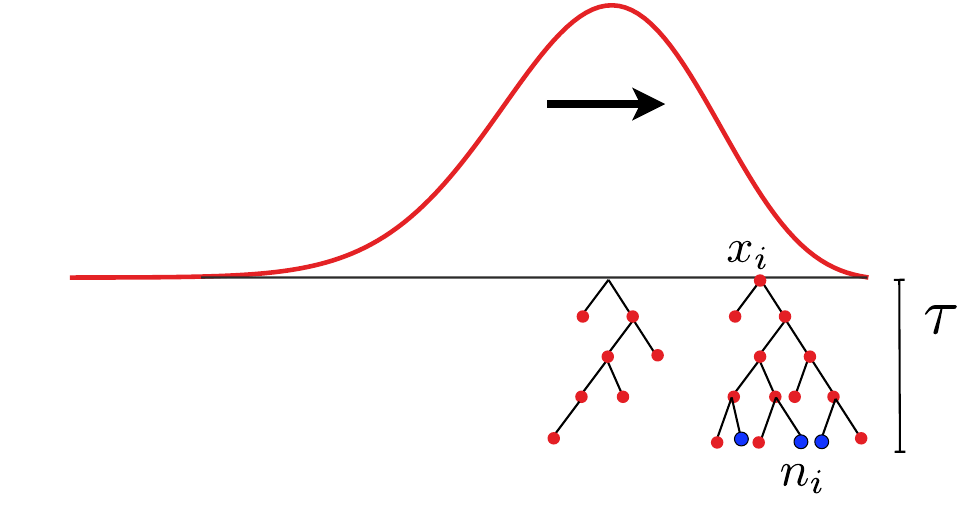
  • Branching process approximation: $P(n_i, t|x_i)$
  • Does a sample (blue dots) have a common ancestor $\tau$ generations ago?
    $\quad Q_b = \langle \sum_i \left(\frac{n_i}{\sum_j n_j}\right)^b\rangle \approx \frac{\tau-T_c}{T_c(b-1)} $
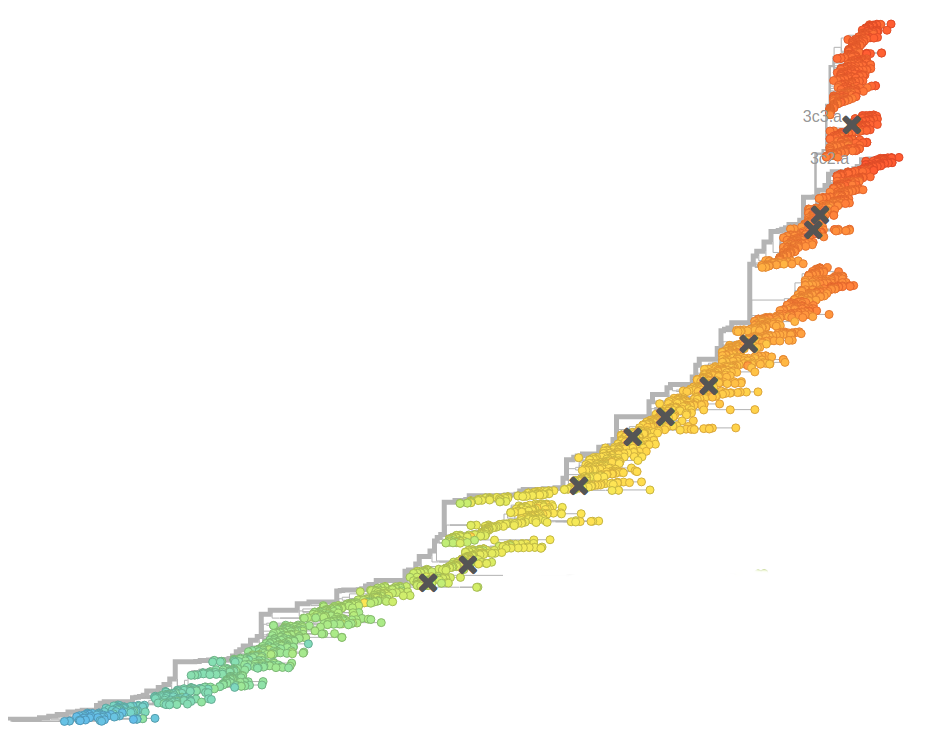
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007

U-shaped polarized site frequency spectra



RN, Hallatschek, PNAS, 2013

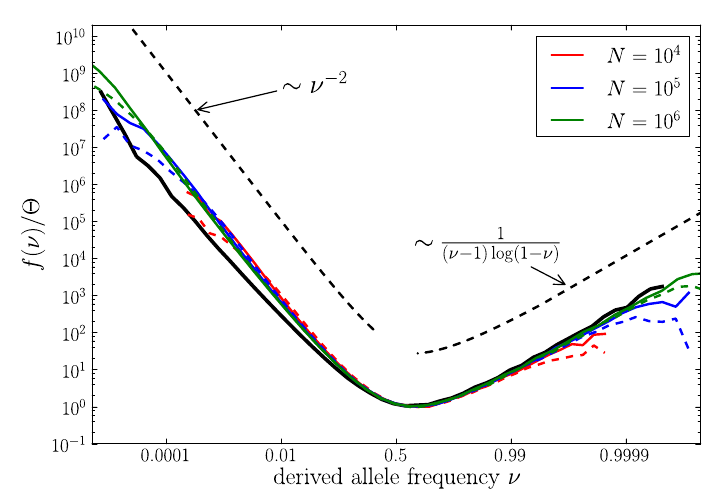
Bursts in a tree ↔ high fitness genotypes

Can we read fitness of a tree?

nextflu.org

joint work with Trevor Bedford & his lab

Predicting evolution

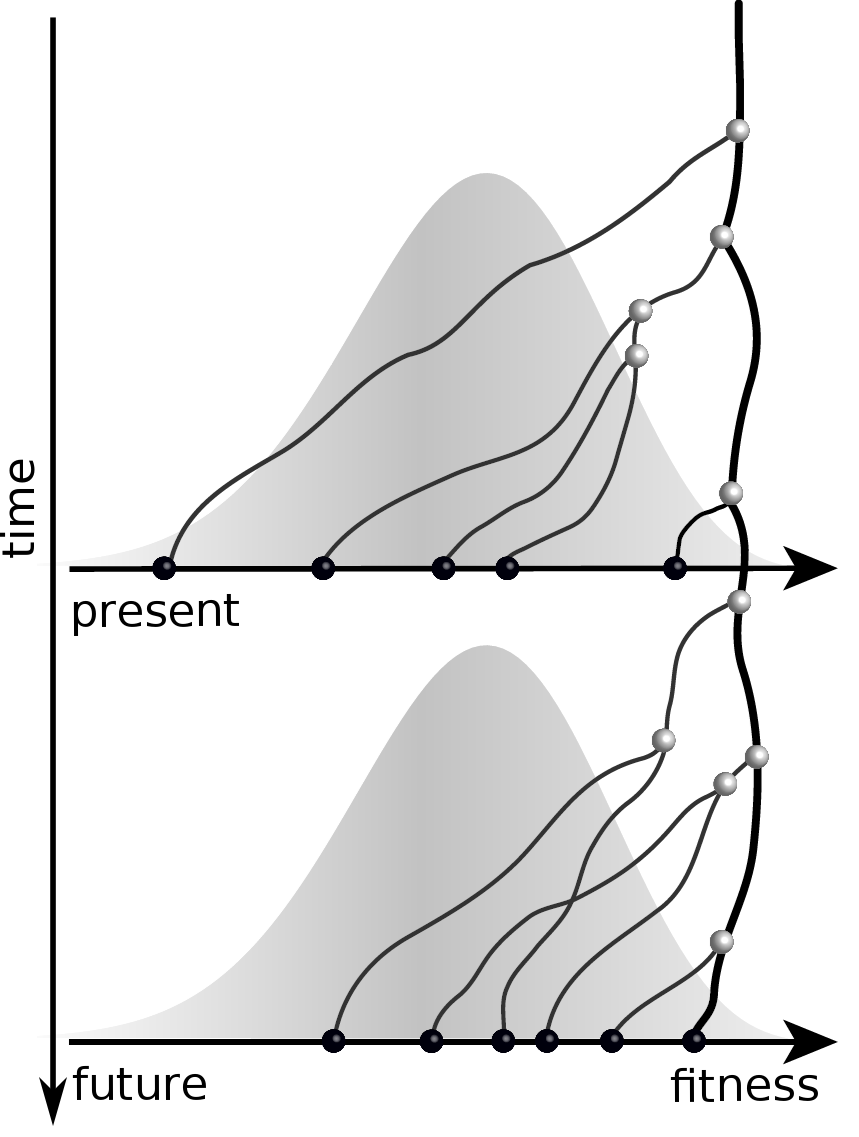
Given the branching pattern:

  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014

Validate on simulation data

  • simulate evolution
  • sample sequences
  • reconstruct trees
  • infer fitness
  • predict ancestor of future
  • compare to truth
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Prediction of the dominating H3N2 influenza strain

  • no influenza specific input
  • how can the model be improved? (see model by Luksza & Laessig)
  • what other context might this apply?
 RN, Russell, Shraiman, eLife, 2014

Summary

  • RNA virus evolution can be observed directly
  • Extensive reversion to preferred amino acid sequence
  • Rapidly adapting population require new population genetic models
  • Those model can be used to infer fit clades
  • Future influenza population can be anticipated
  • Automated real-time analysis can help fight the spread of disease

Acknowledgments

  • Fabio Zanini
  • Jan Albert
  • Johanna Brodin
  • Christa Lanz
  • Göran Bratt
  • Lina Thebo
  • Vadim Puller

Acknowlegdements

  • Trevor Bedford
  • Colin Megill
  • Pavel Sagulenko
  • Sidney Bell
  • James Hadfield
  • Wei Ding
  • Emma Hodcroft
  • Sanda Dejanic

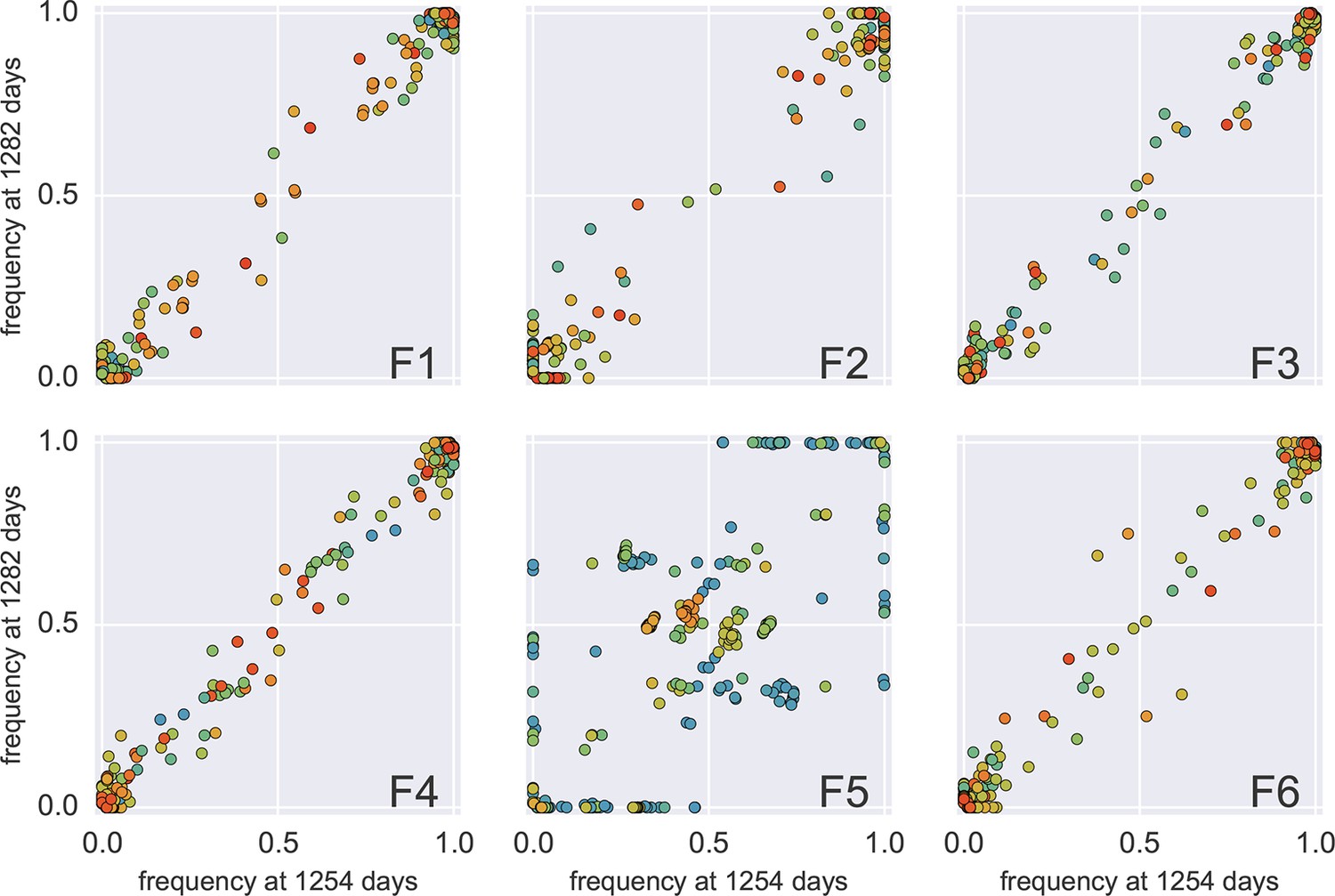
Amplification bias and template input

Accuracy of minor variant frequencies

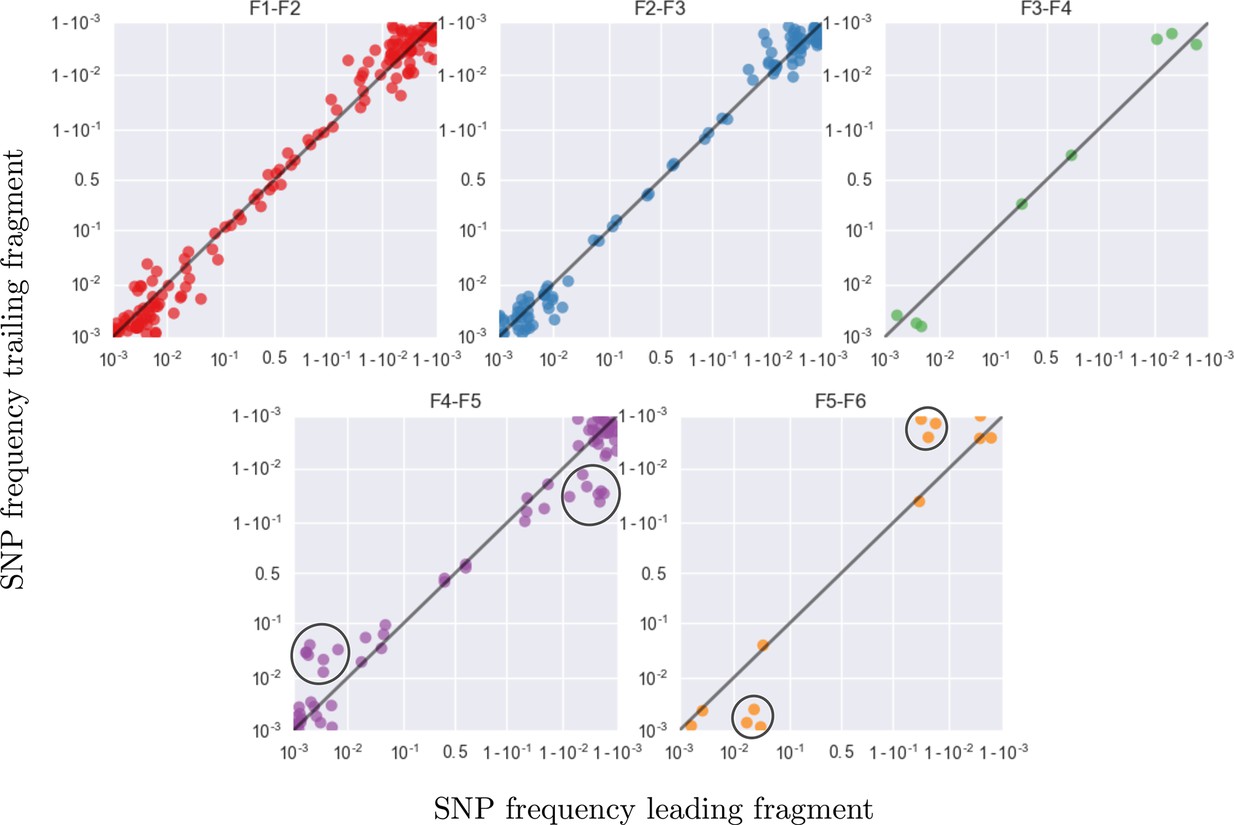
Frequency concordance in samples 4 weeks apart

The distribution of fitness costs

Zanini et al, Virus Evolution, 2017

Fitness costs vs consensus amino acid

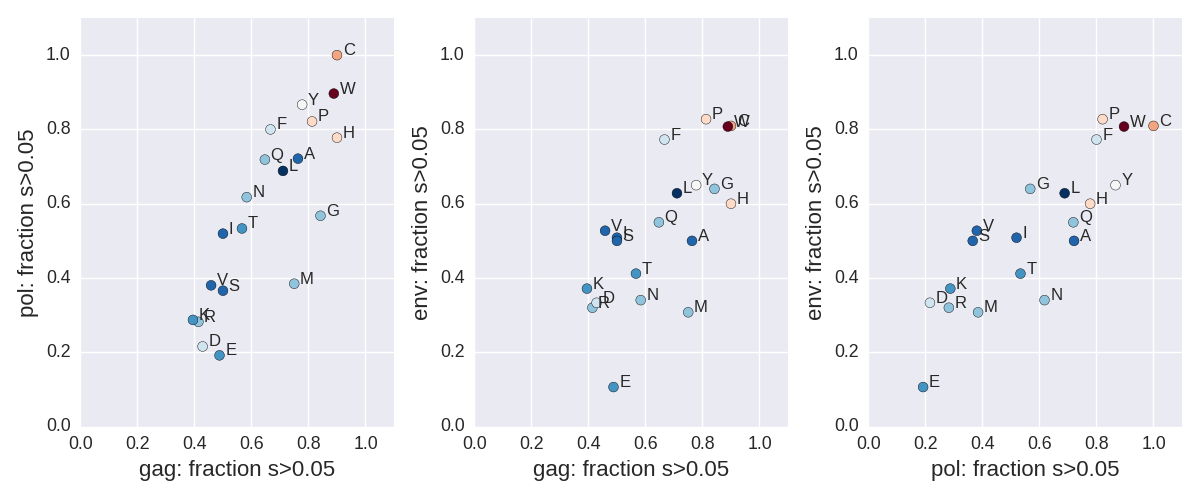Zanini et al, Virus Evolution, 2017

Frequent reversion of previously beneficial mutations

  • HIV escapes immune systems
  • most mutations are costly
  • humans selects for different mutations
  • compensation or reversion?
Zanini et al, eLife, 2015

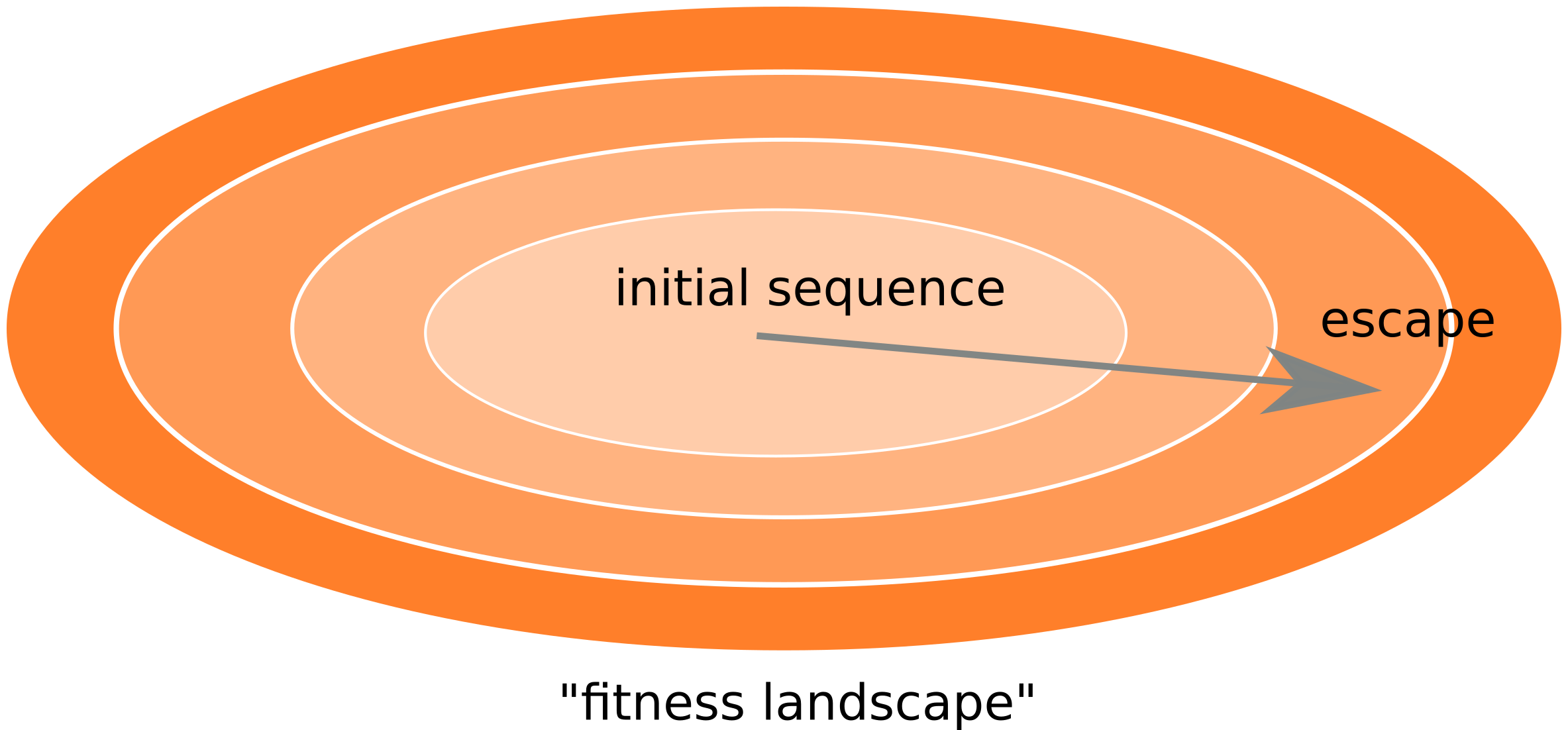
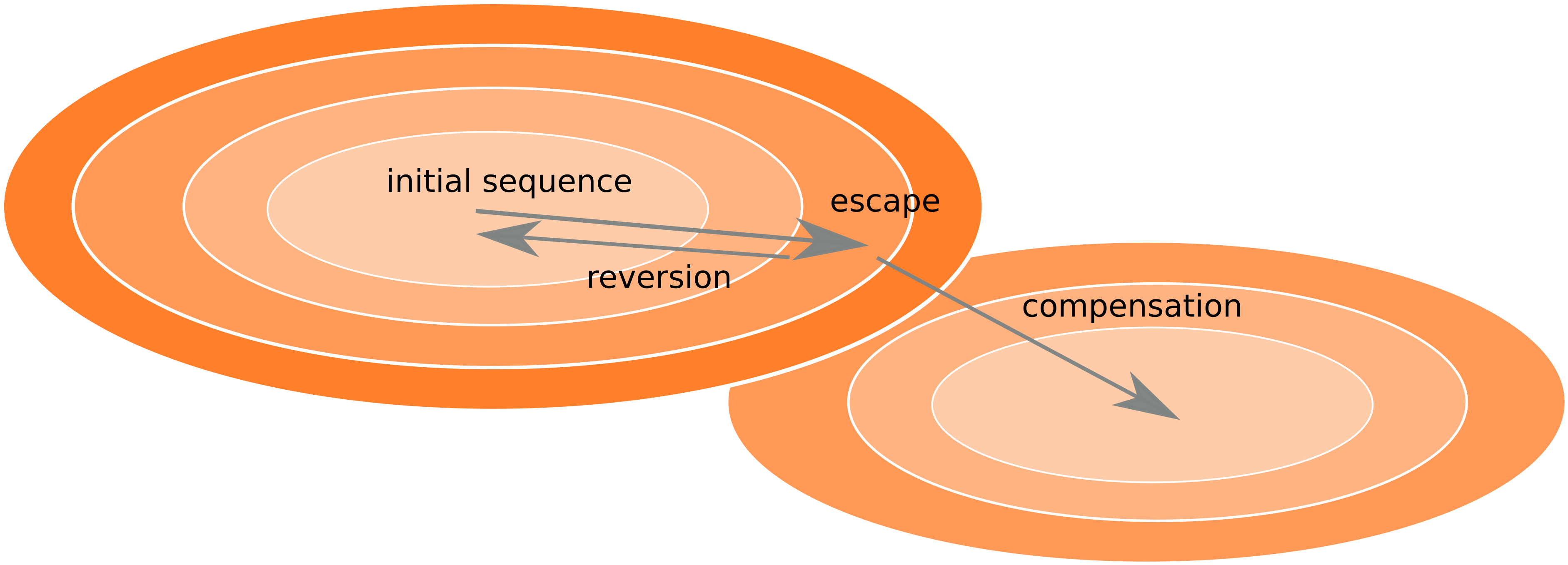
Accurate frequency estimates by averaging many samples

  • Frequencies of costly mutations decorrelate fast $\frac{d x}{dt} = \mu -s x $
  • $\Rightarrow$ average many samples to obtain accurate estimates