Virus evolution and the spread of infectious disease
Richard Neher
Biozentrum, University of Basel
slides at neherlab.org/20181212_Ringvorlesung.html
Viruses
 tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
tobacco mosaic virus
(Thomas Splettstoesser, wikipedia)
bacteria phage (adenosine, wikipedia)
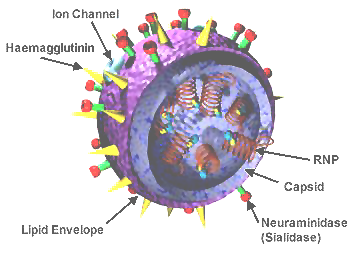
influenza virus wikipedia
human immunodeficiency virus wikipedia
- rely on host to replicate
- little more than genome + capsid
- genomes typically 5-200k bases (+exceptions)
- most abundant organisms on earth $\sim 10^{31}$
Lifecycle of animal viruses
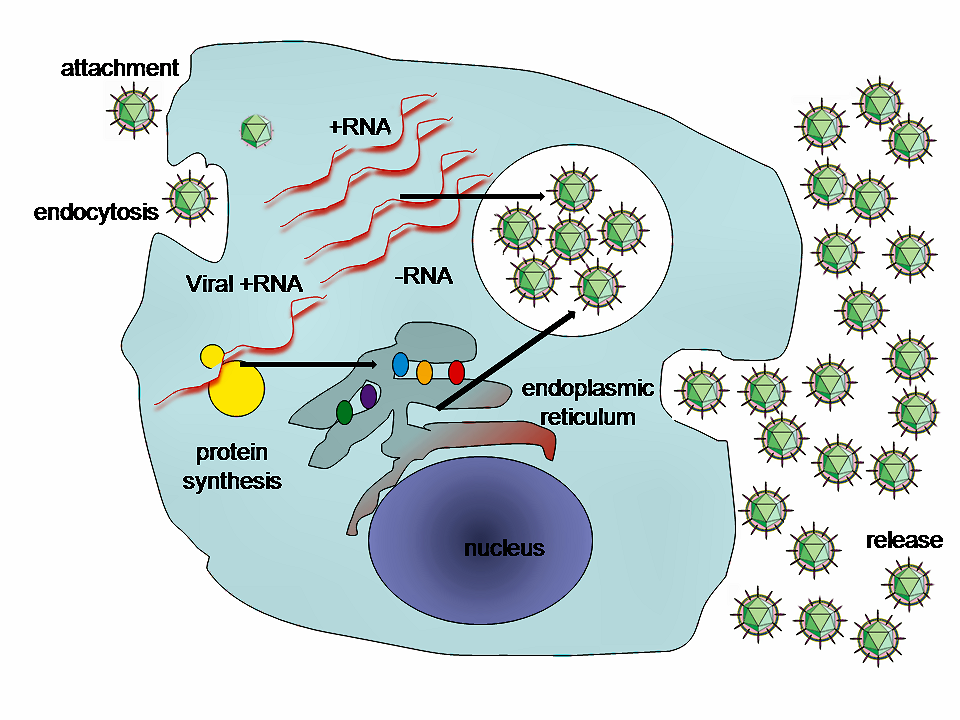 By GrahamColm at English Wikipedia
By GrahamColm at English Wikipedia
Development of sequencing technologies
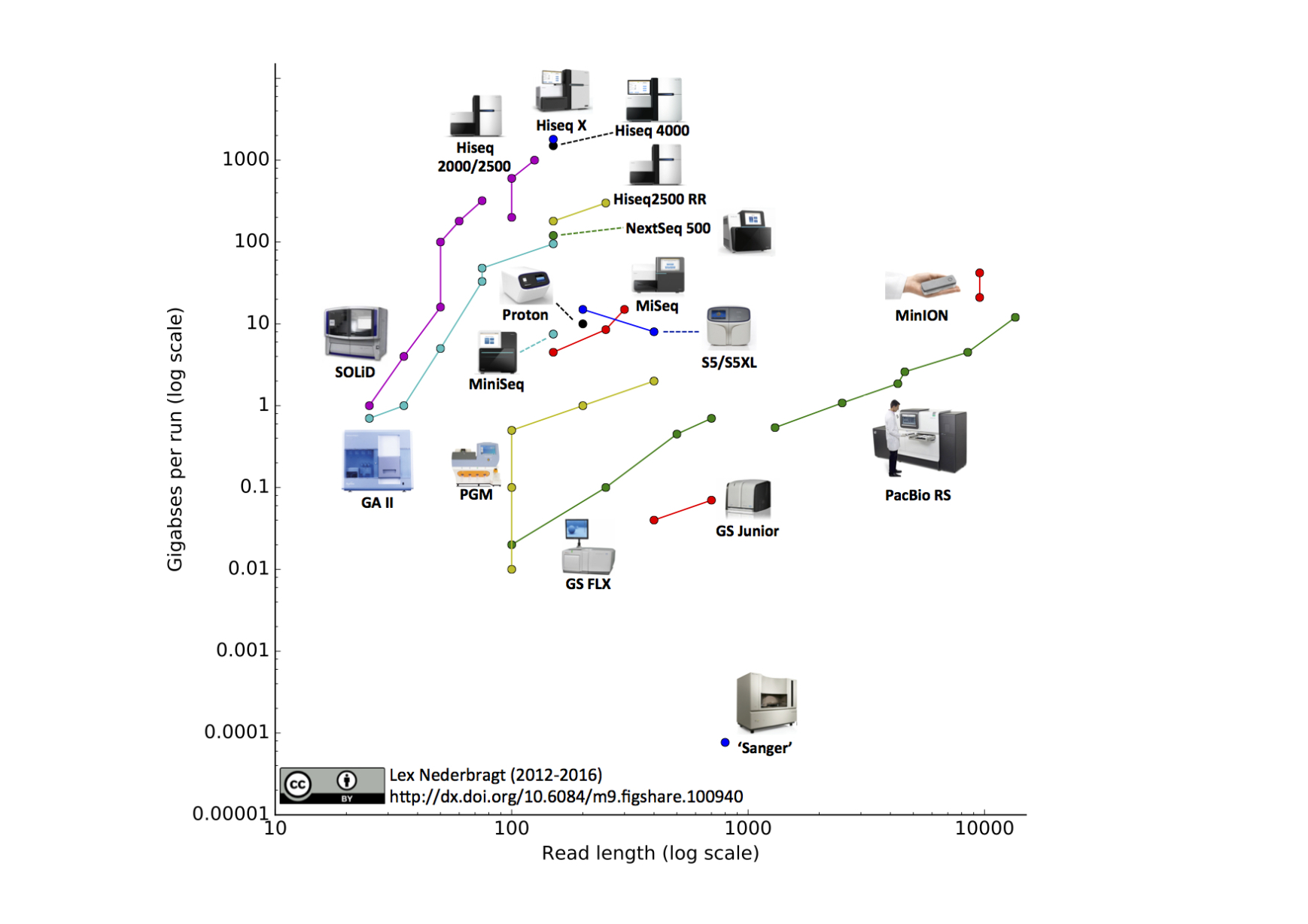
We can now sequence...
- thousands of bacterial isolates
- thousands of single cells
- populations of viruses, bacteria or flies
- diverse ecosystems
Viral sequences
A/Brisbane/100/2014
GGATAATTCTATTAACCATGAAGACTATCATTGCTTT...
A/Brisbane/1000/2015
GGATAATTCTATTAACCATGAAGACTATTATTGCTTT...
A/Brisbane/1/2017
GGATAATTCTATTAACCATGAAGACTATCATTGCTTT...
... thousands of sequences...
GGATAATTCTATTAACCATGAAGACTATCATTGCTTT...
A/Brisbane/1000/2015
GGATAATTCTATTAACCATGAAGACTATTATTGCTTT...
A/Brisbane/1/2017
GGATAATTCTATTAACCATGAAGACTATCATTGCTTT...
... thousands of sequences...
Phylogenetic analysis of viral sequences
RNA viruses have a high mutation rate. New mutations arise every few weeks.
Some viruses evolve a million times faster than animals
Animal haemoglobin

HIV protein

Evolution of HIV
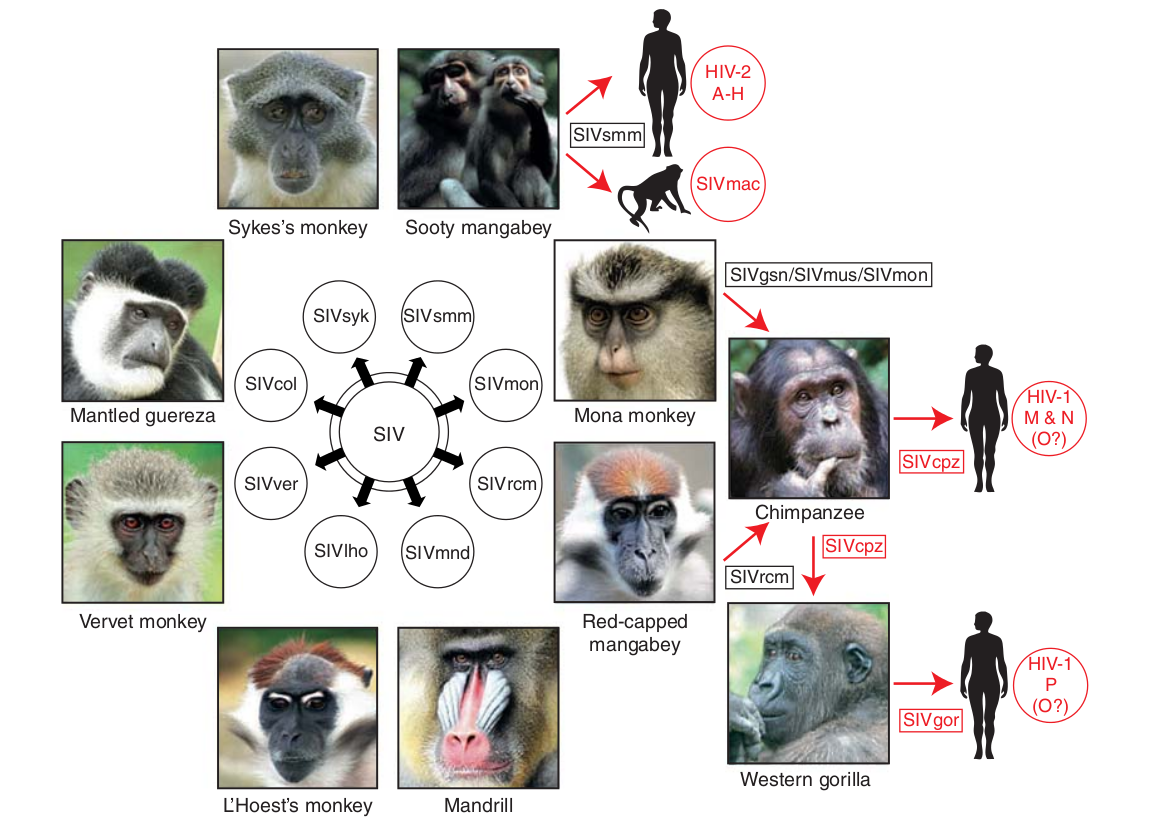
- Chimp → human transmission around 1900 gave rise to HIV-1 group M
- ~100 million infected people since
- subtypes differ at 10-20% of their genome
- HIV-1 evolves ~0.1% per year
HIV infection
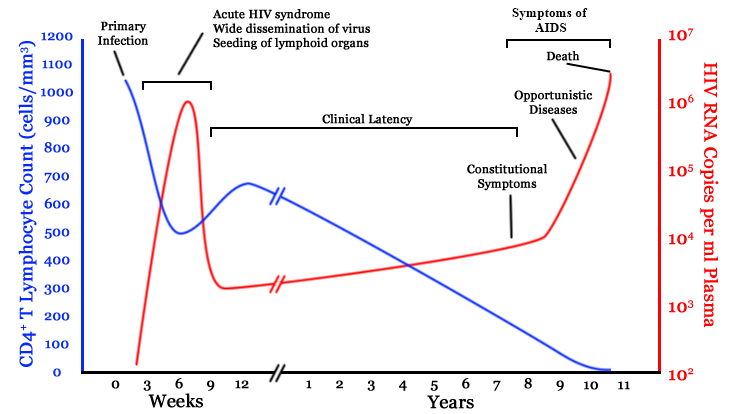
- $10^8$ cells are infected every day
- the virus repeatedly escapes immune recognition
- integrates into T-cells as
latent provirus
HIV-1 evolution within one individual
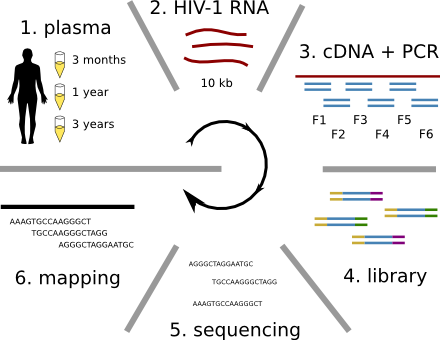

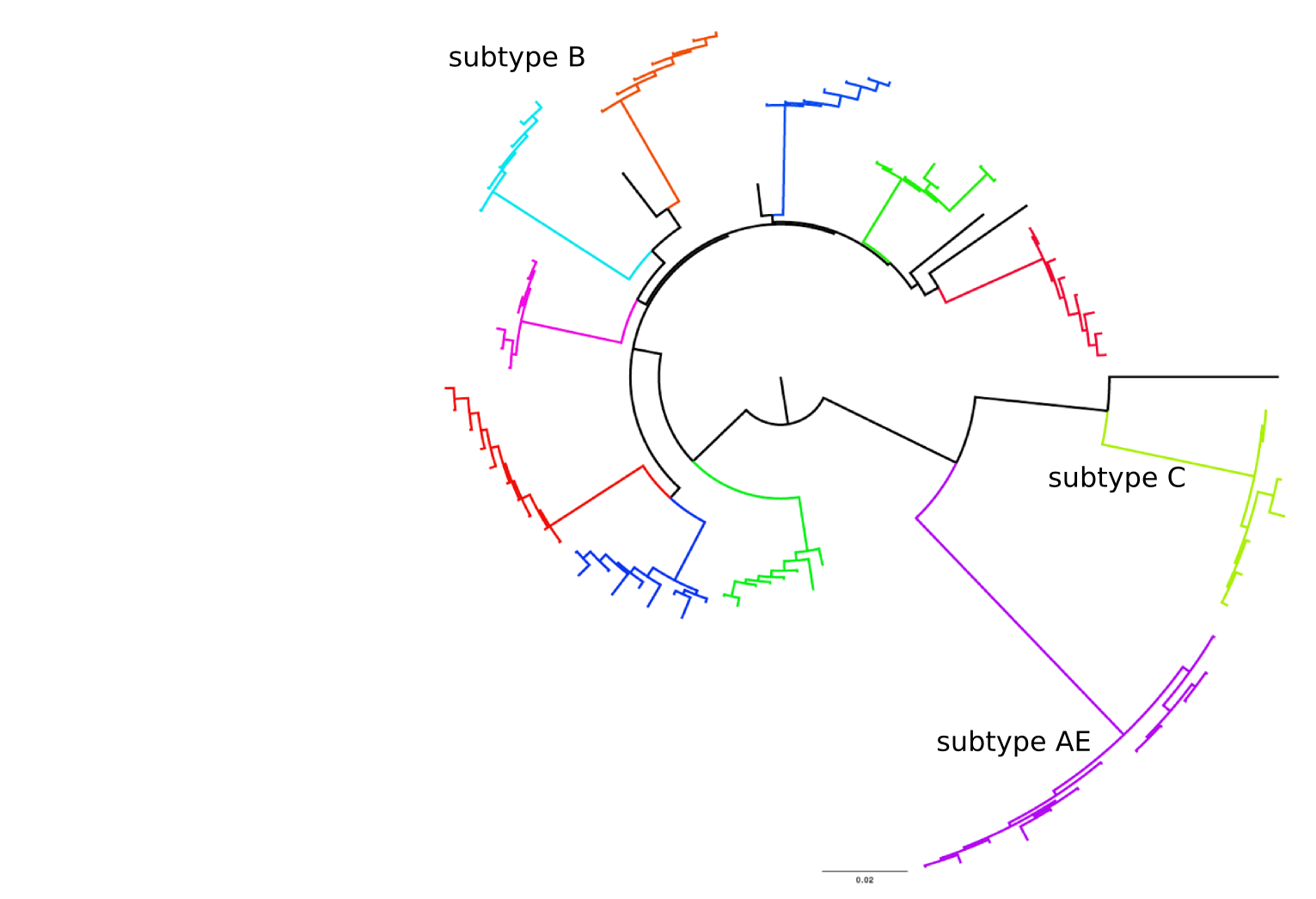
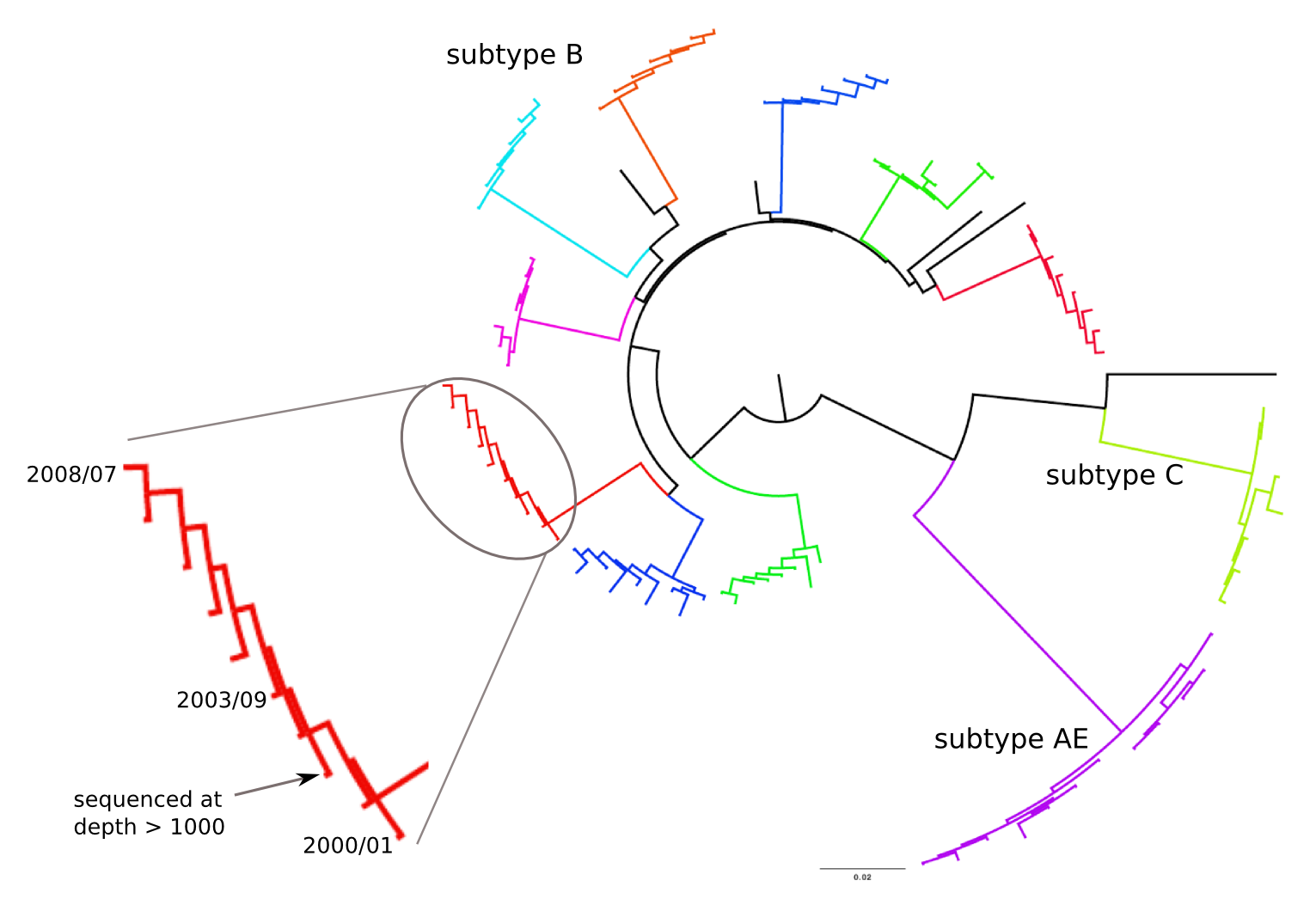
Immune escape in early HIV infection
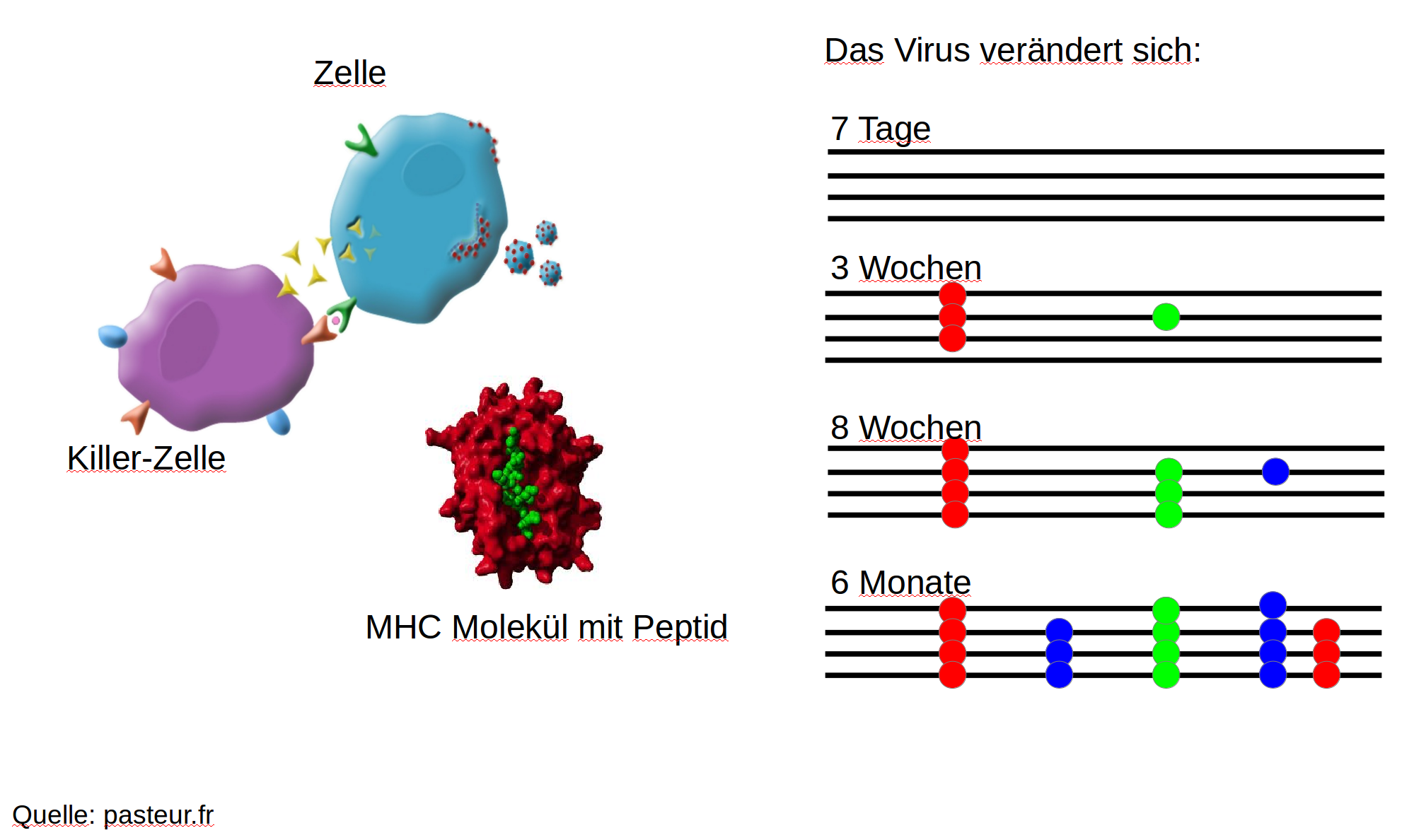
Immune escape in early HIV infection
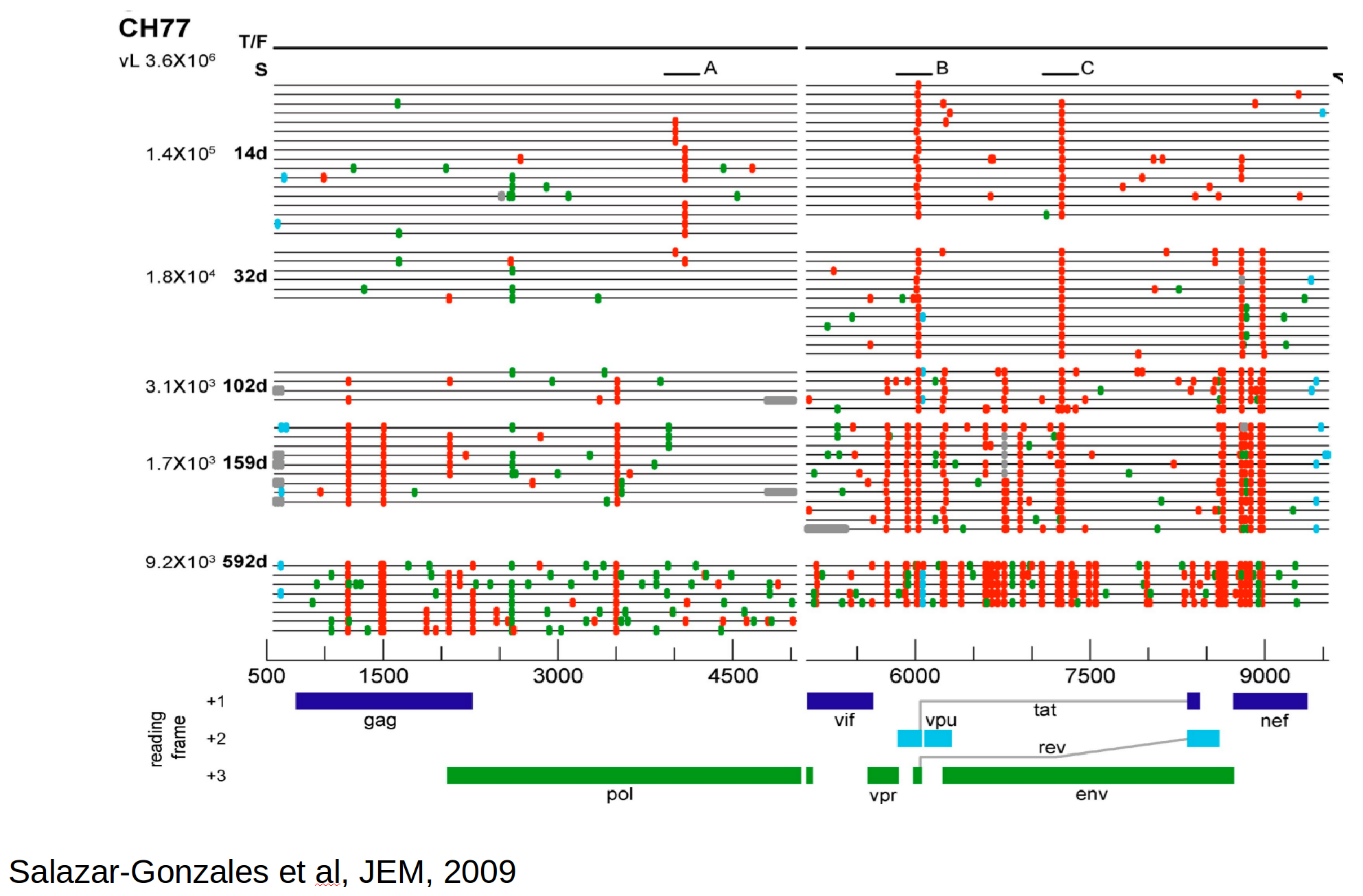
Population genetics & evolutionary dynamics
evolutionary processes ↔ trees ↔ genetic diversity
Selective sweeps
- Viruses carrying a beneficial mutation have more offspring: on average $1+s$ instead of $1$
- $s$ is called selection coefficient
- Fraction $x$ of viruses carrying the mutation changes as $$x(t+1) = \frac{(1+s)x(t)}{(1+s)x(t) + (1-x(t))}$$
- In continuous time → logistic differential equation: $$\frac{dx}{dt} = sx(1-x) \Rightarrow x(t) = \frac{e^{s(t-t_0)}}{1+ e^{s(t-t_0)}}$$
Population sequencing to track all mutations above 1%
- diverge at 0.1-1% per year
- almost whole genome coverage in 10 patients
- full data set at hiv.tuebingen.mpg.de
The rate of sequence evolution in HIV
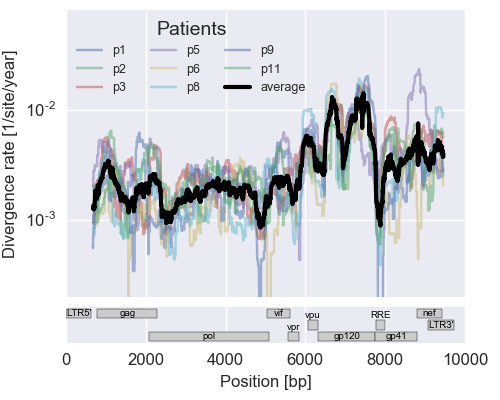
Mutation rates and diversity and neutral sites
Inference of fitness costs
- mutation away from preferred state with rate $\mu$
- selection against non-preferred state with strength $s$
- variant frequency dynamics: $\frac{d x}{dt} = \mu -s x $
- equilibrium frequency: $\bar{x} = \mu/s $
- fitness cost: $s = \mu/\bar{x}$
Fitness landscape of HIV-1
Zanini et al, Virus Evolution, 2017Human Influenza A viruses
Weekly numbers of positive influenza tests in the US by subtype
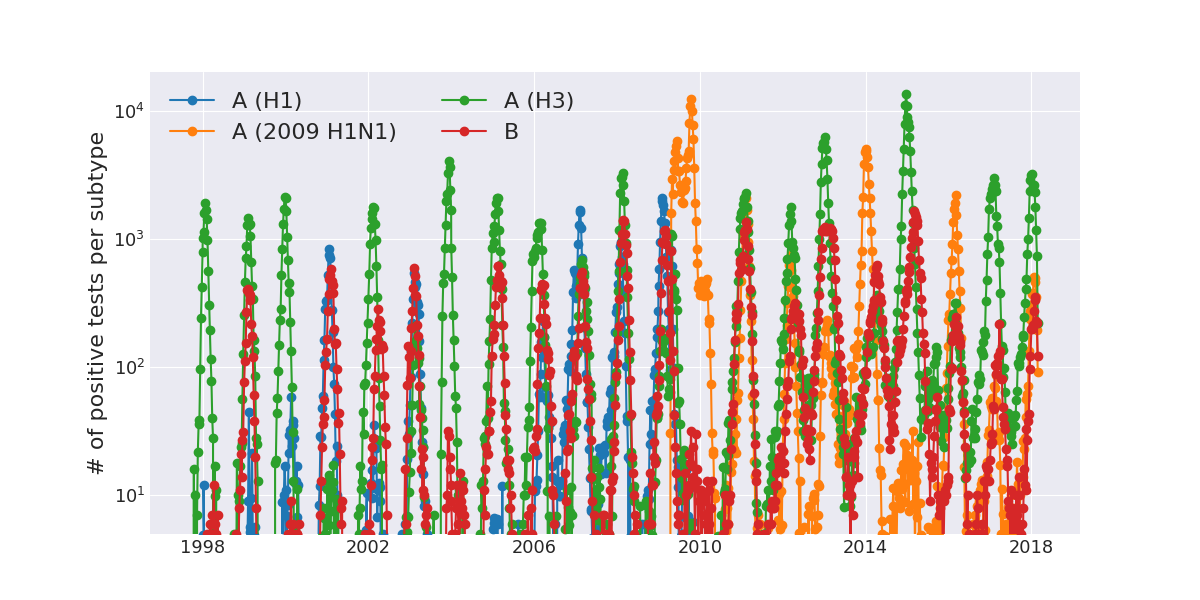 Data by the US CDC
Data by the US CDC
Influenza virus
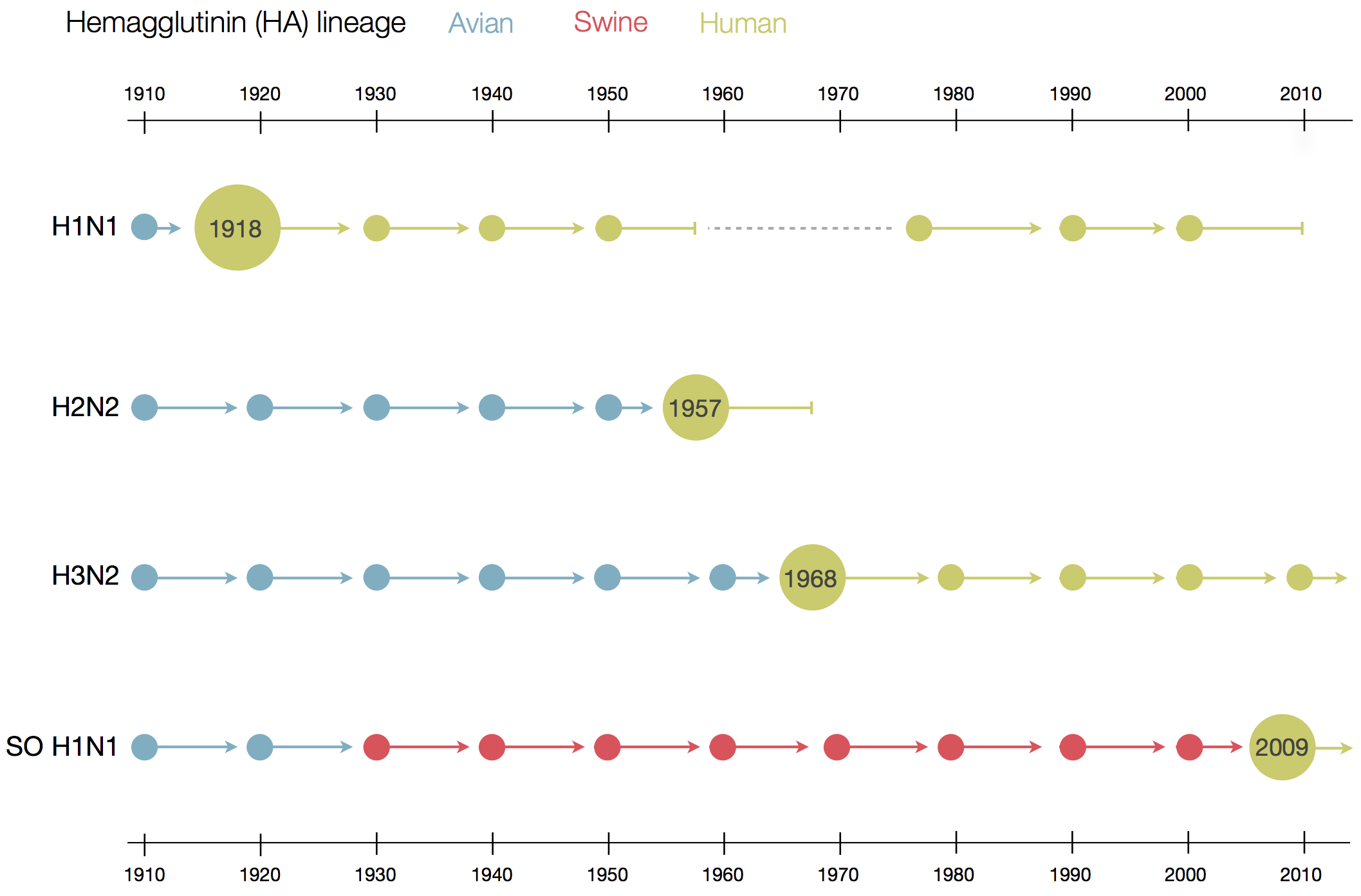
- Surface proteins hemagglutinin (HA) and neuraminidase (NA)
- Influenza A virus
- Common in birds and mammals
- Many different subtypes defined by surface proteins
- H3N2, H1N1, H7N9, H5N1
- Influenza B virus
- infects mainly humans
- two lineages that split 30-40y ago
- B/Victoria vs B/Yamagata
nextflu.org
joint work with Trevor Bedford & his lab
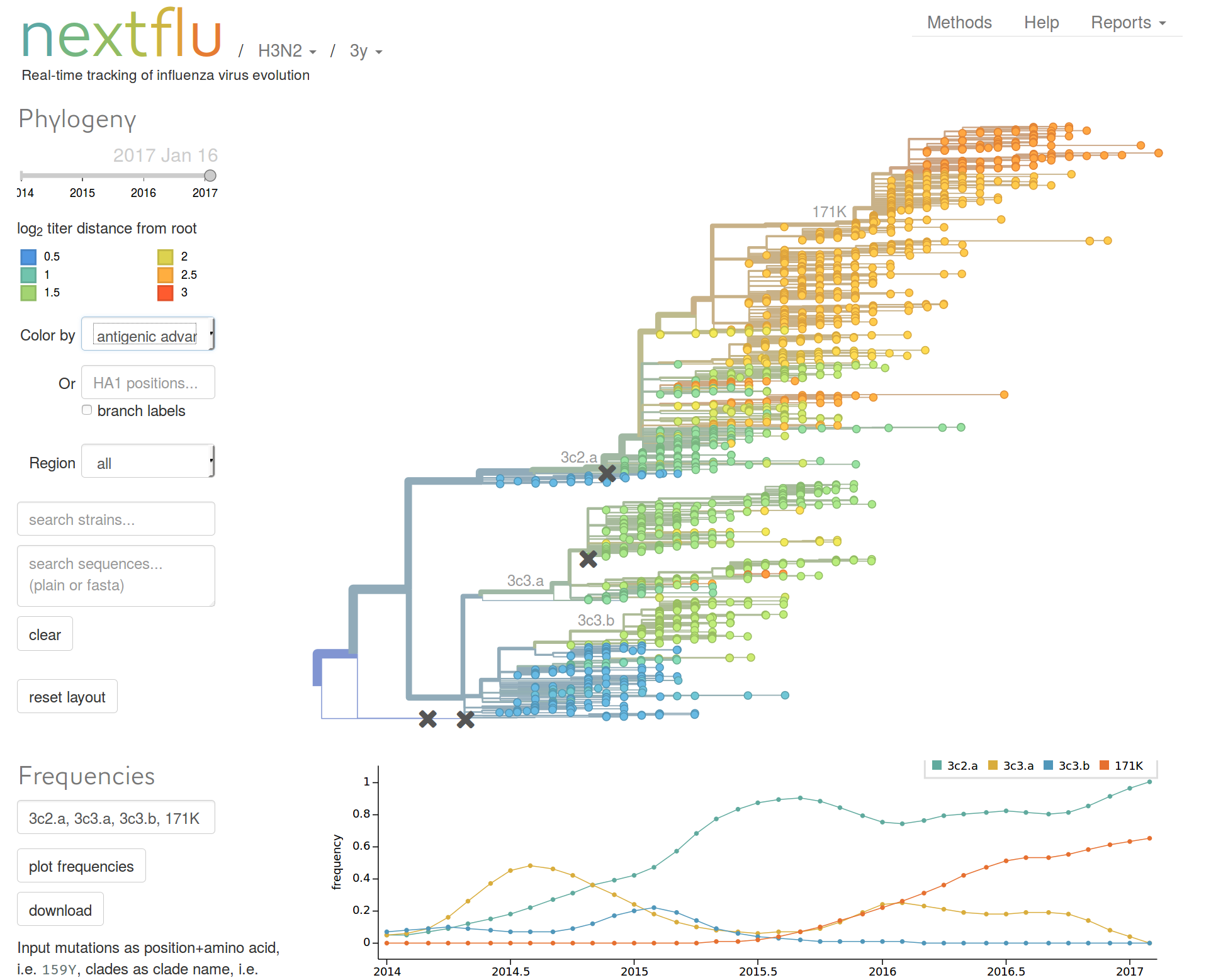
nextstrain.org
joint work with Trevor Bedford & his lab
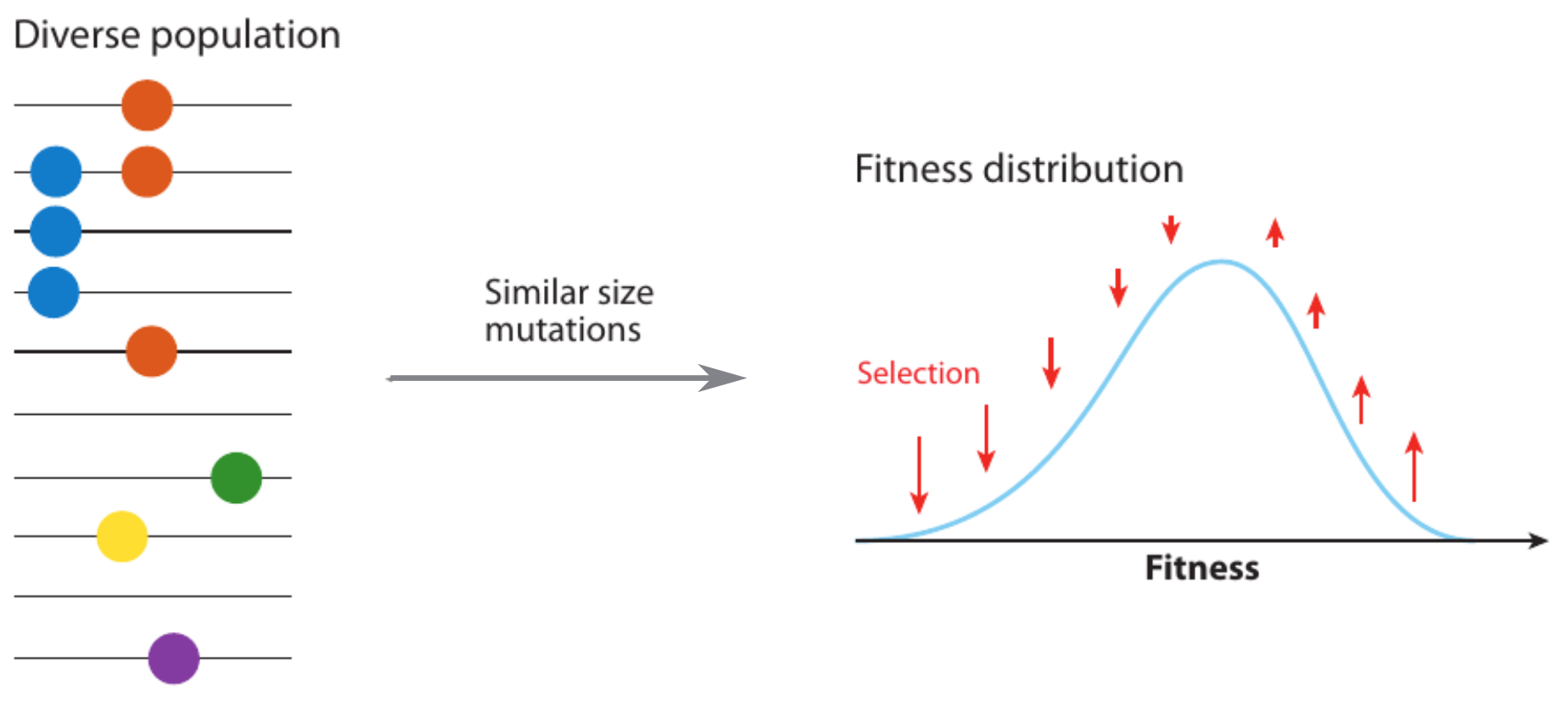
Clonal interference and traveling waves
Typical tree
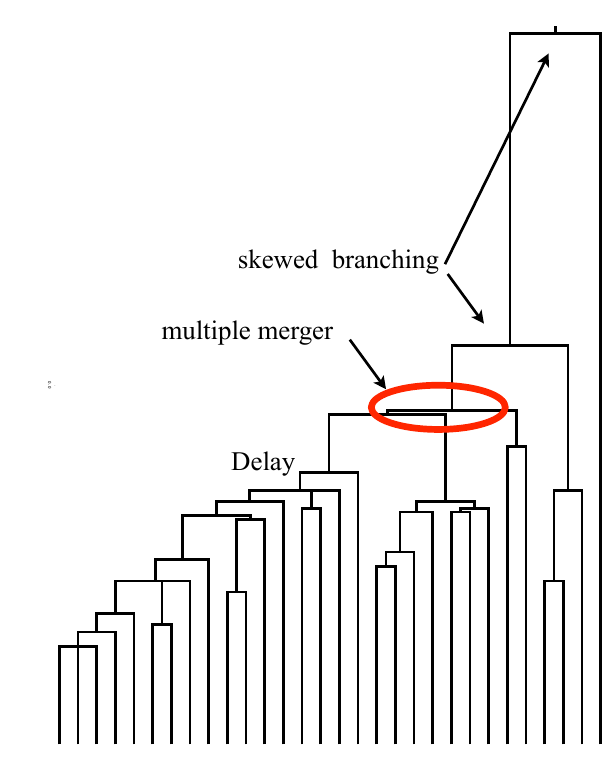
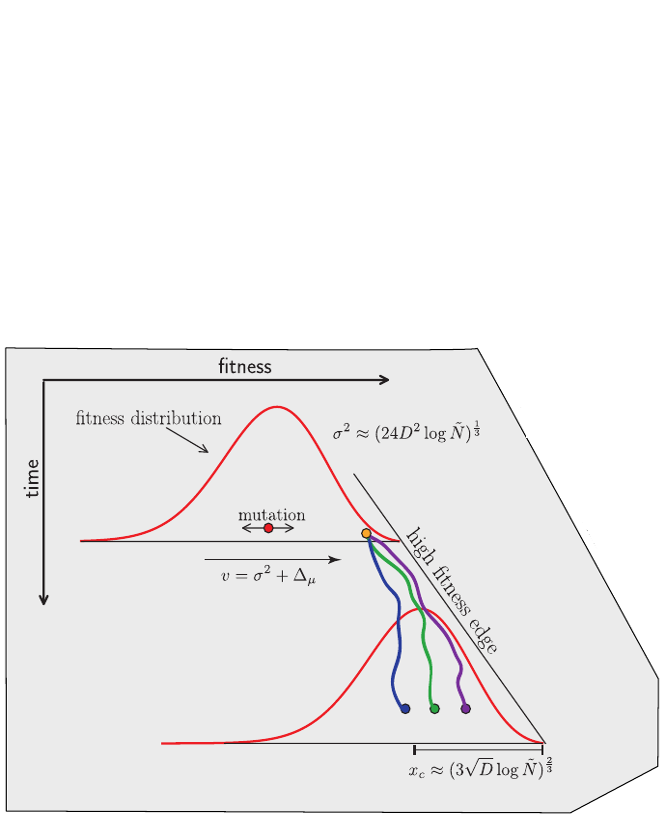
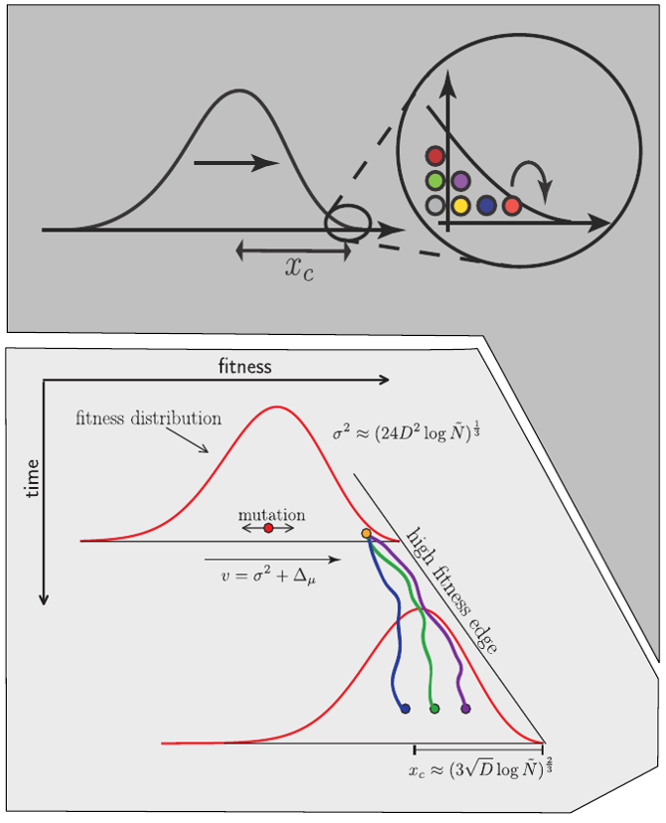
Bolthausen-Sznitman Coalescent
Bursts in a tree ↔ high fitness genotypes
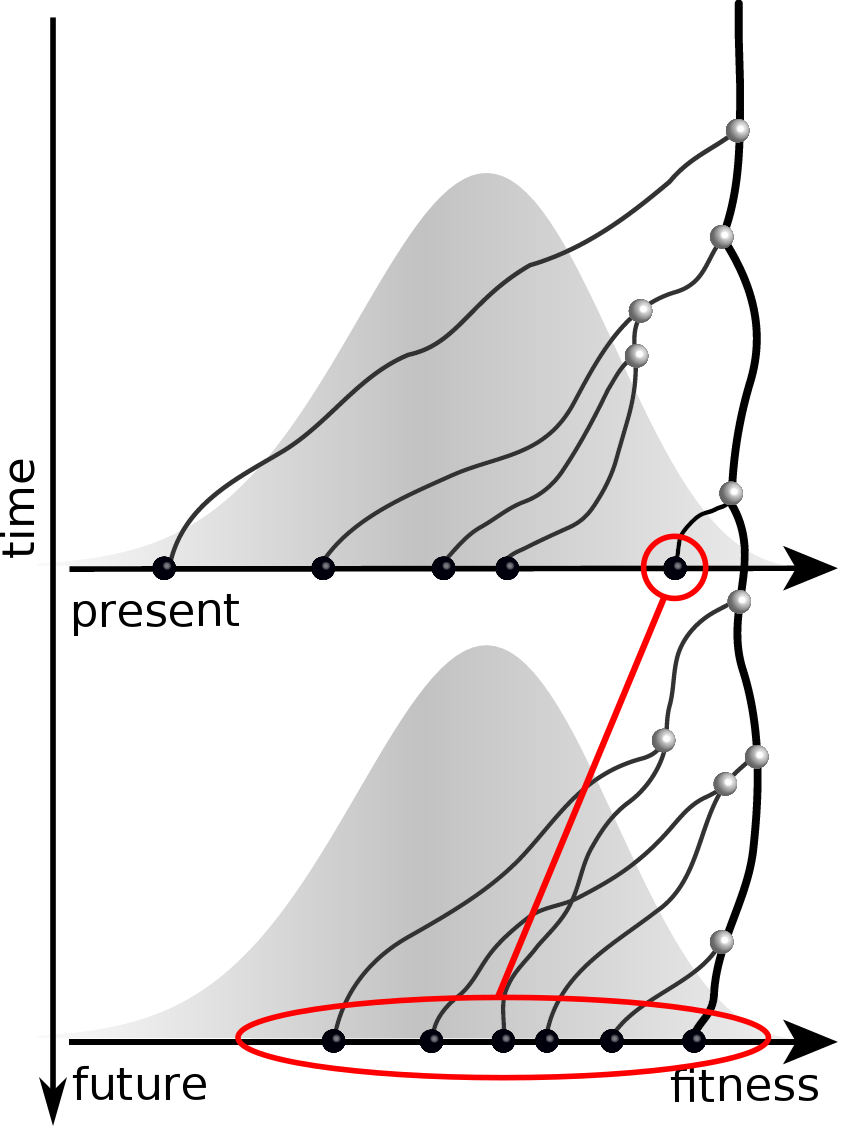
Can we read fitness of a tree?
Predicting evolution
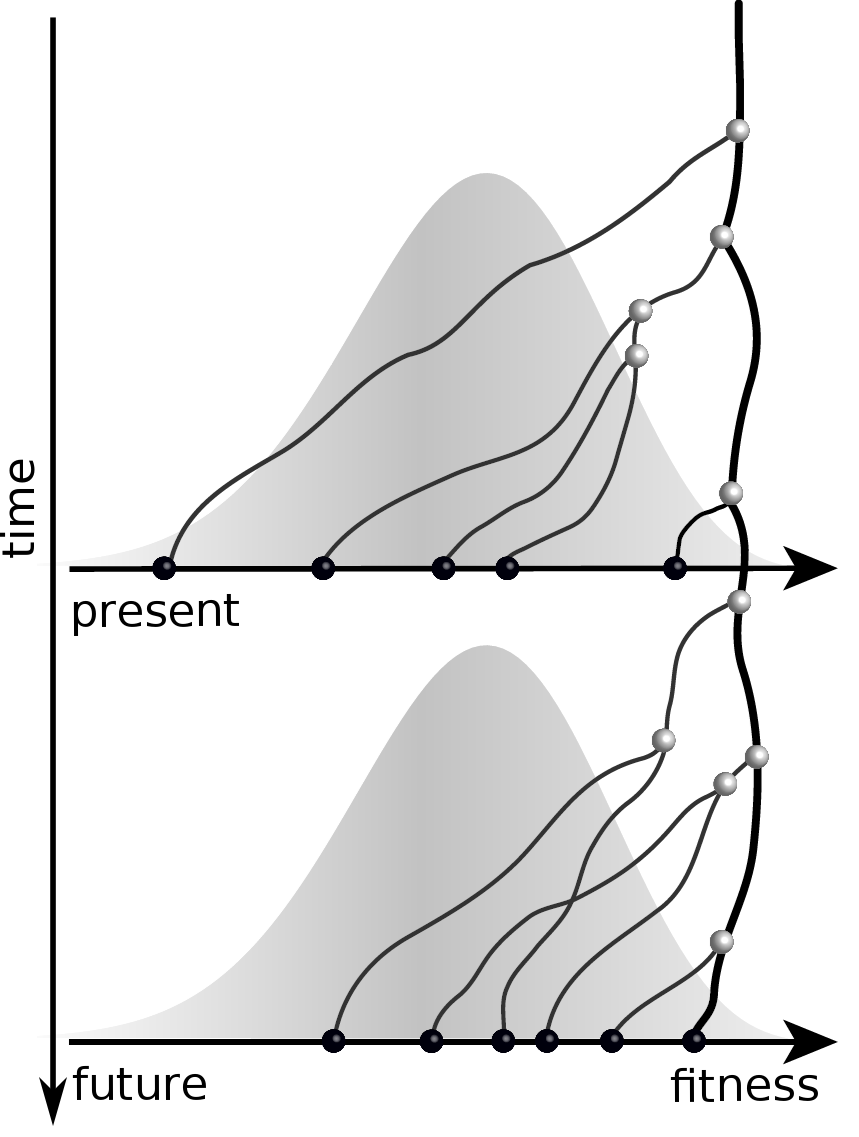
Given the branching pattern:
- can we predict fitness?
- pick the closest relative of the future?
Fitness inference from trees
$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$
RN, Russell, Shraiman, eLife, 2014
Validation on simulated data
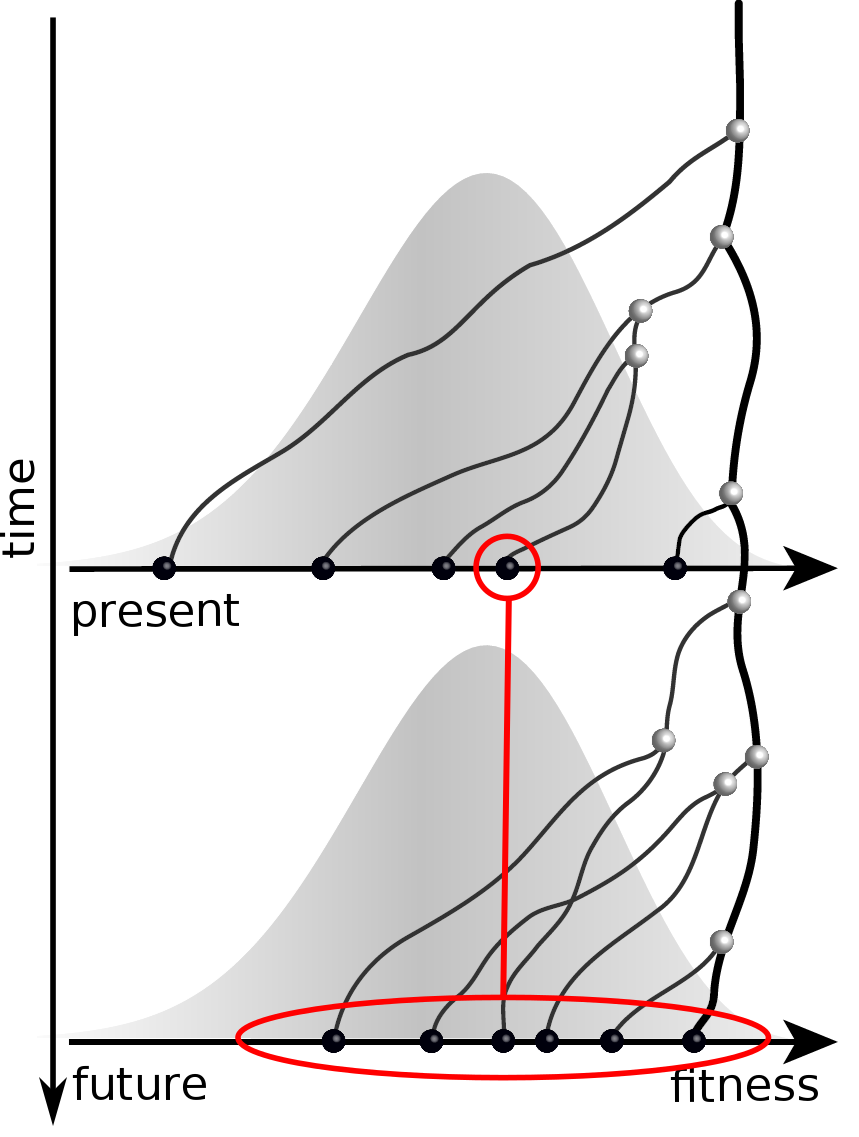
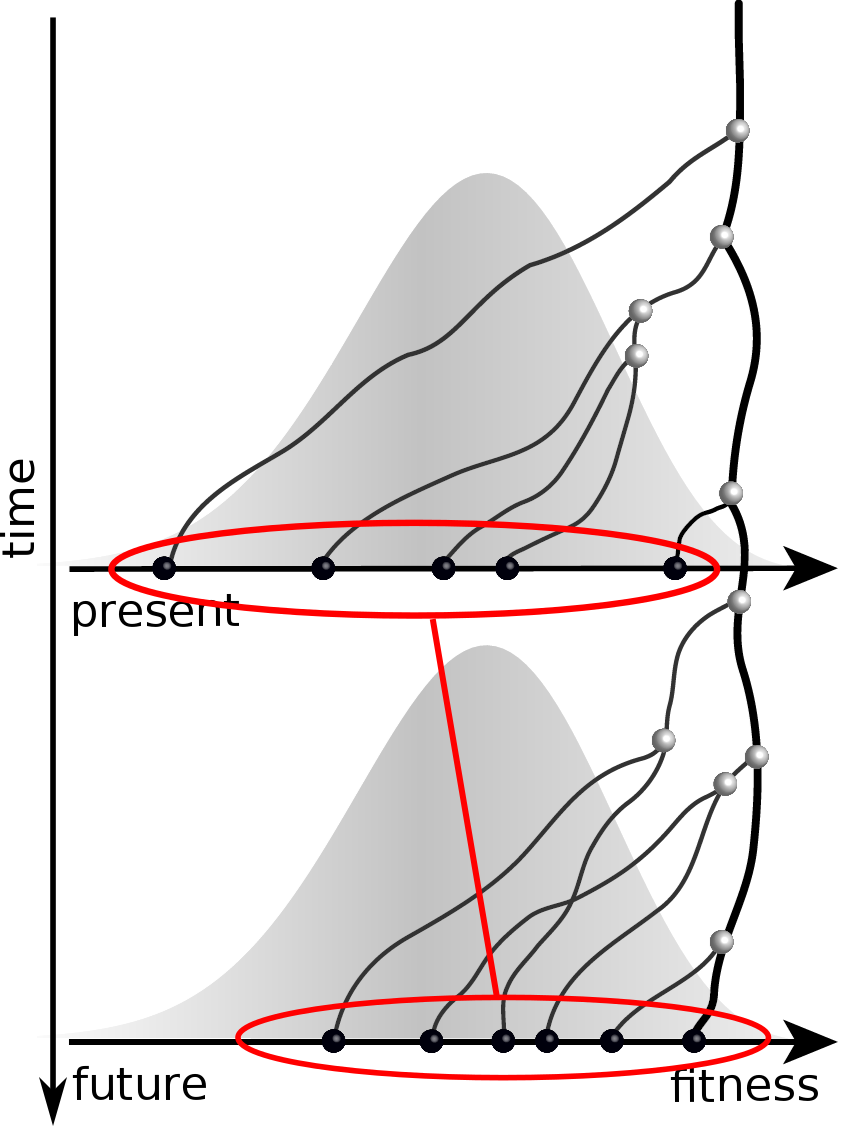
Prediction of the dominating H3N2 influenza strain
- no influenza specific input
- how can the model be improved? (see model by Luksza & Laessig)
- what other context might this apply?
Summary
- RNA virus evolution can be observed directly
- Rapidly adapting population require new population genetic models
- Those model can be used to infer fit clades
- Future influenza population can be anticipated
- Automated real-time analysis can help fight the spread of disease
HIV acknowledgments







- Fabio Zanini
- Jan Albert
- Johanna Brodin
- Christa Lanz
- Göran Bratt
- Lina Thebo
- Vadim Puller



Influenza and Theory acknowledgments




- Boris Shraiman
- Colin Russell
- Trevor Bedford
- Oskar Hallatschek



Acknowledgments






- Trevor Bedford
- Colin Megill
- Pavel Sagulenko
- Sidney Bell
- James Hadfield
- Wei Ding
- Emma Hodcroft
- Sanda Dejanic



