RNA virus evolution and the predictability of next year's flu
Richard Neher
Biozentrum, University of Basel
slides at neherlab.org/201903_APS.html
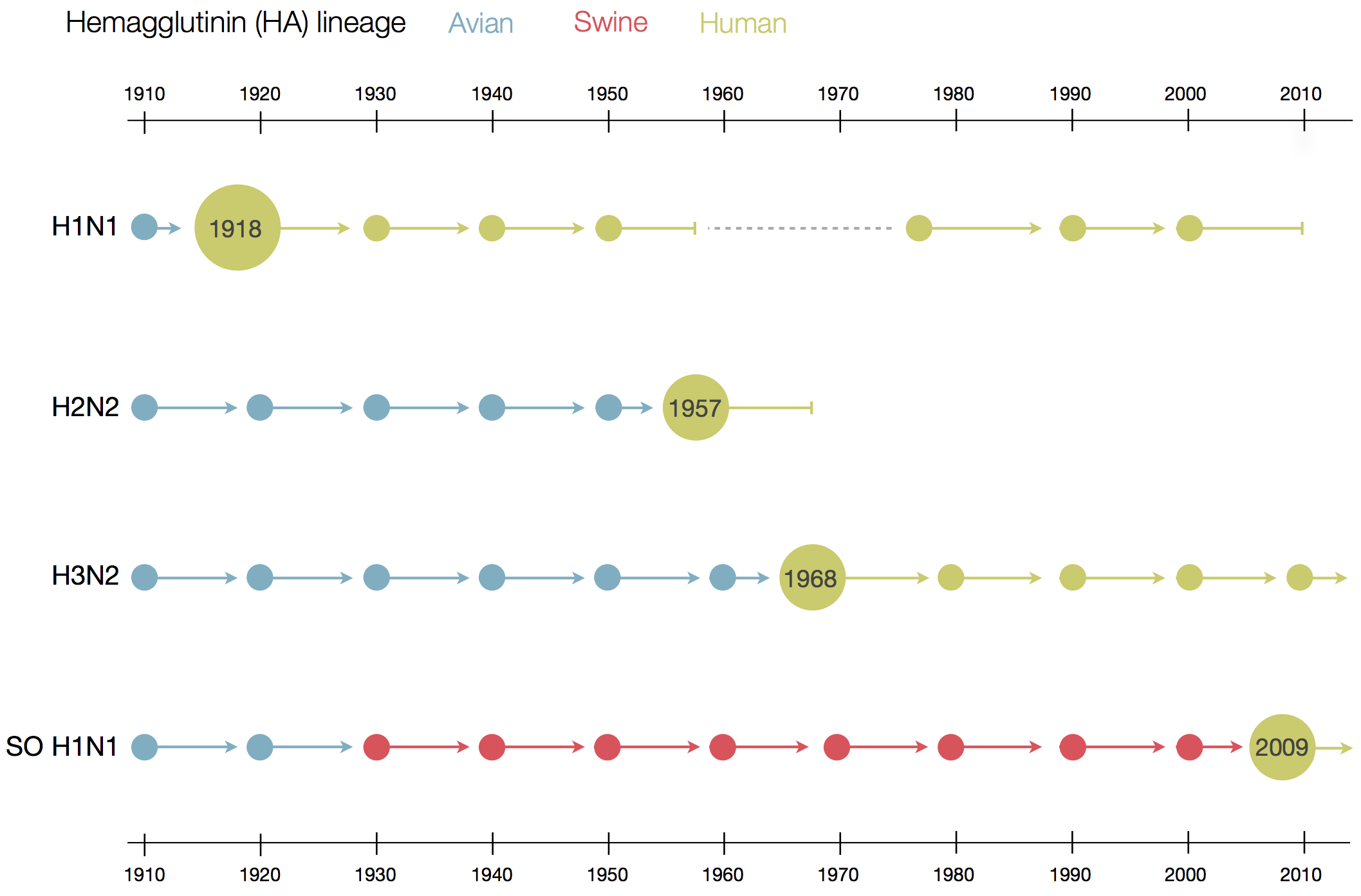
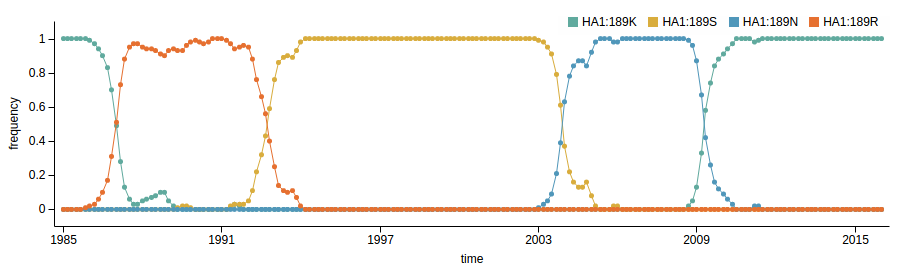
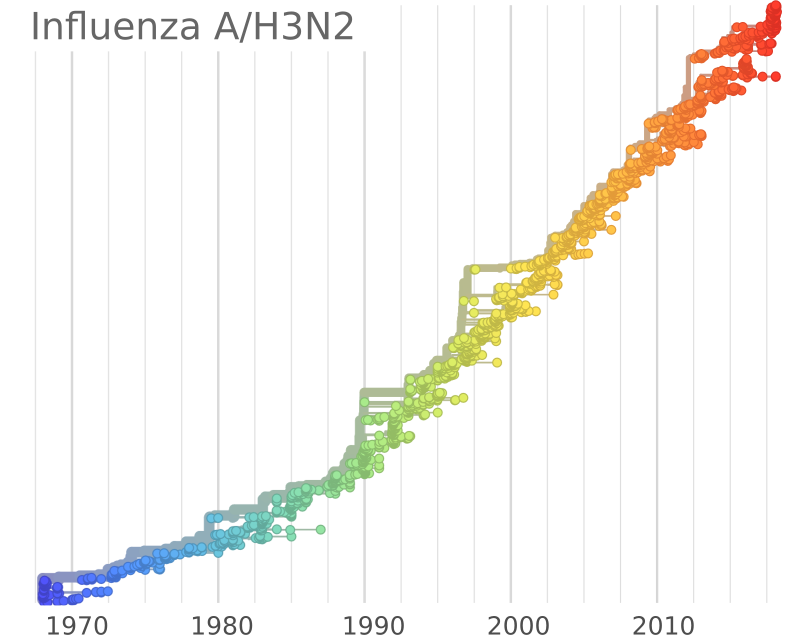
Human seasonal influenza viruses
Sequences record the spread of pathogens
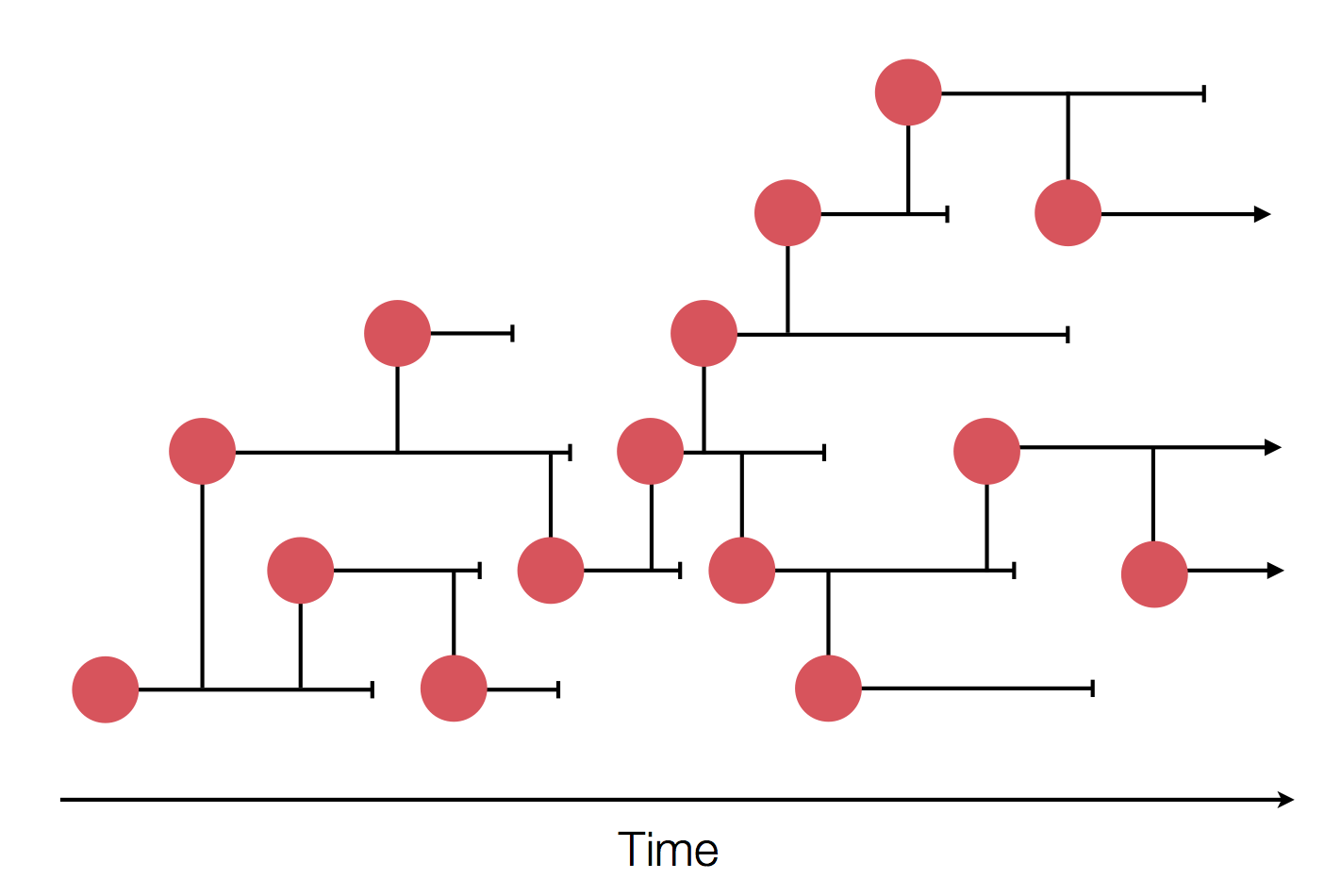
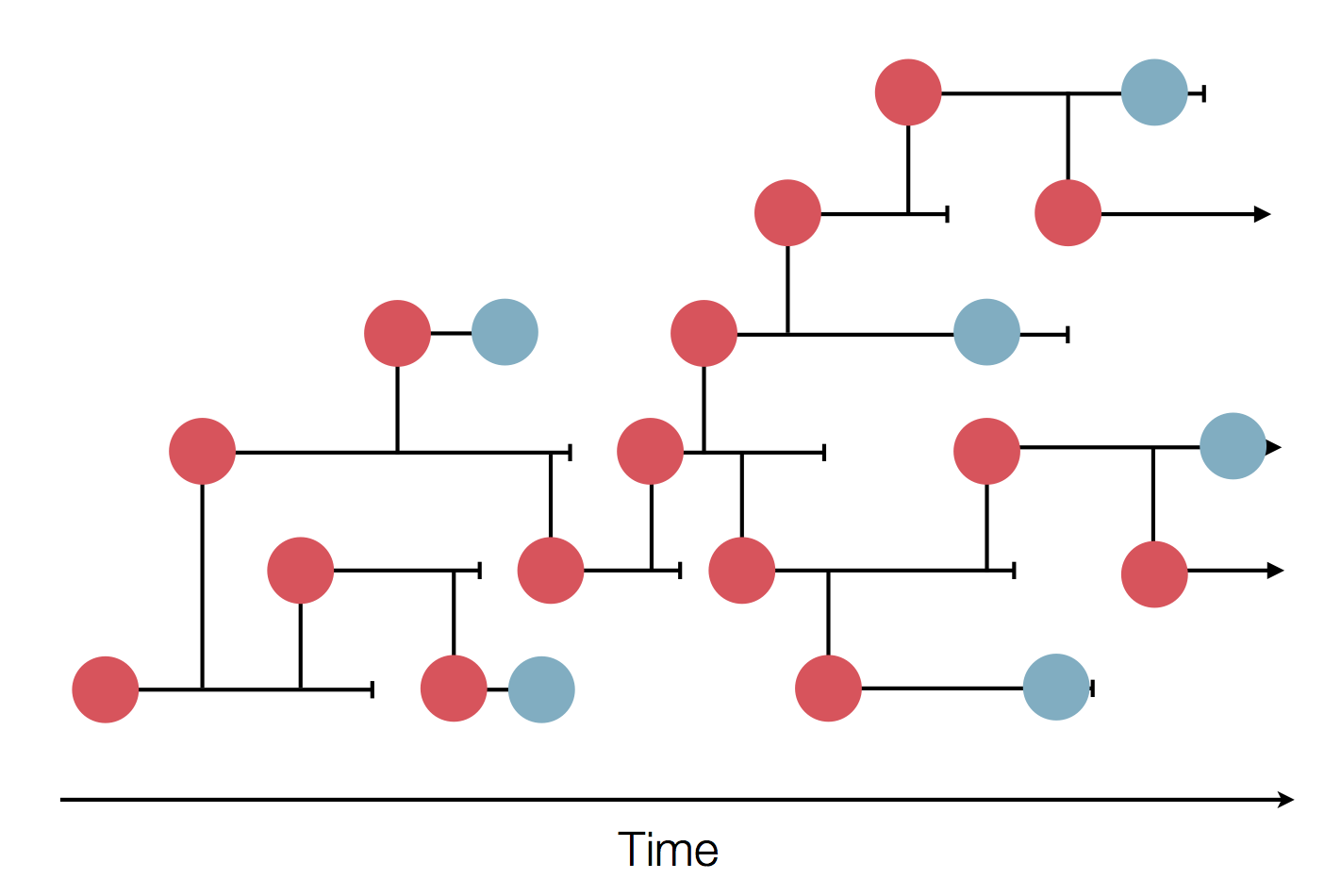
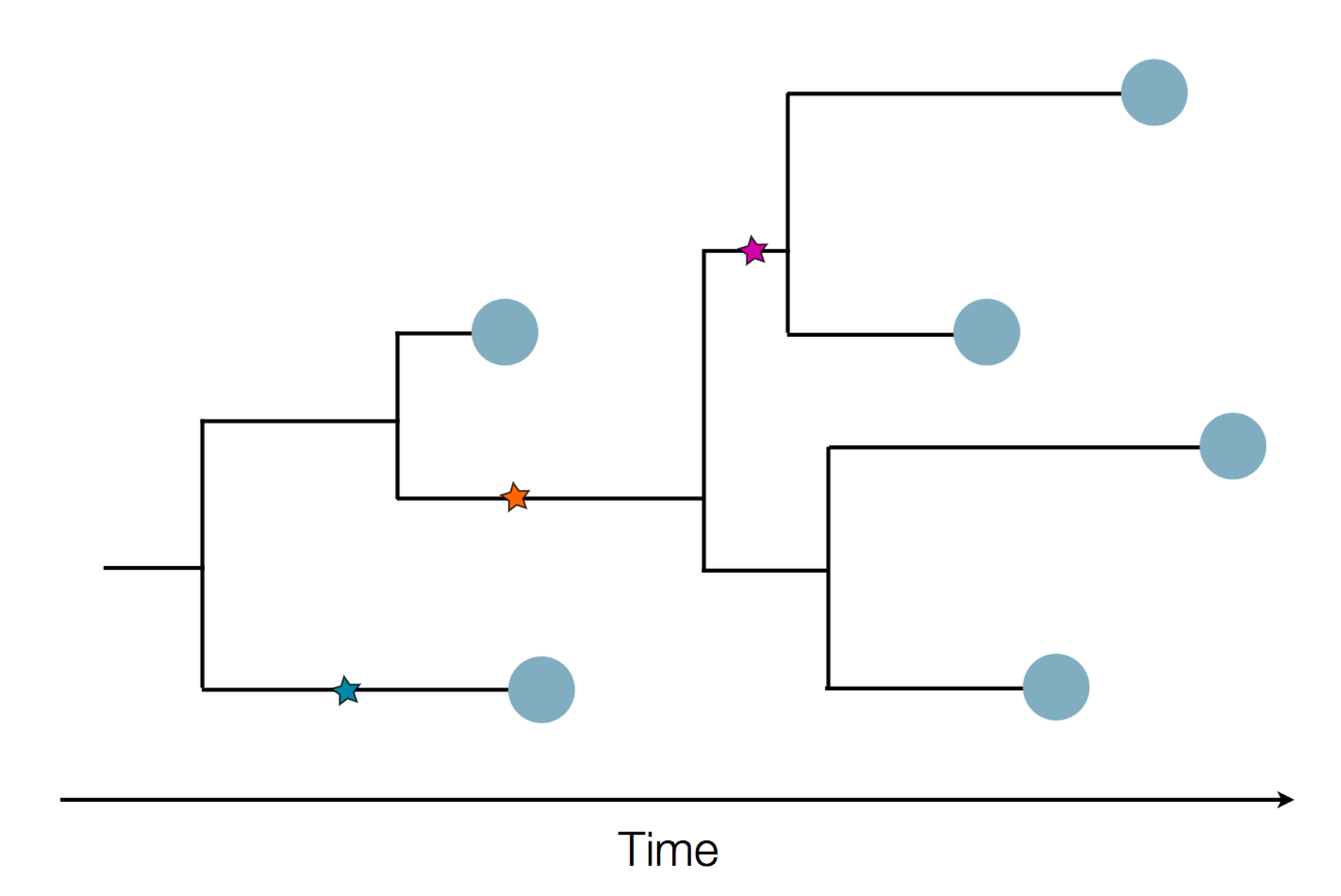
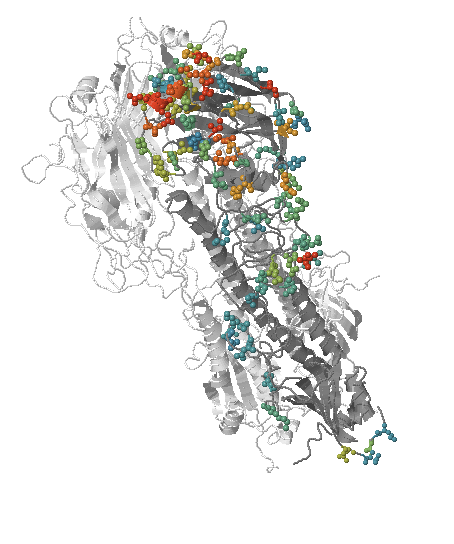
- Influenza virus evolves to avoid human immunity
- Vaccines need frequent updates
Vaccine strain selection schedule
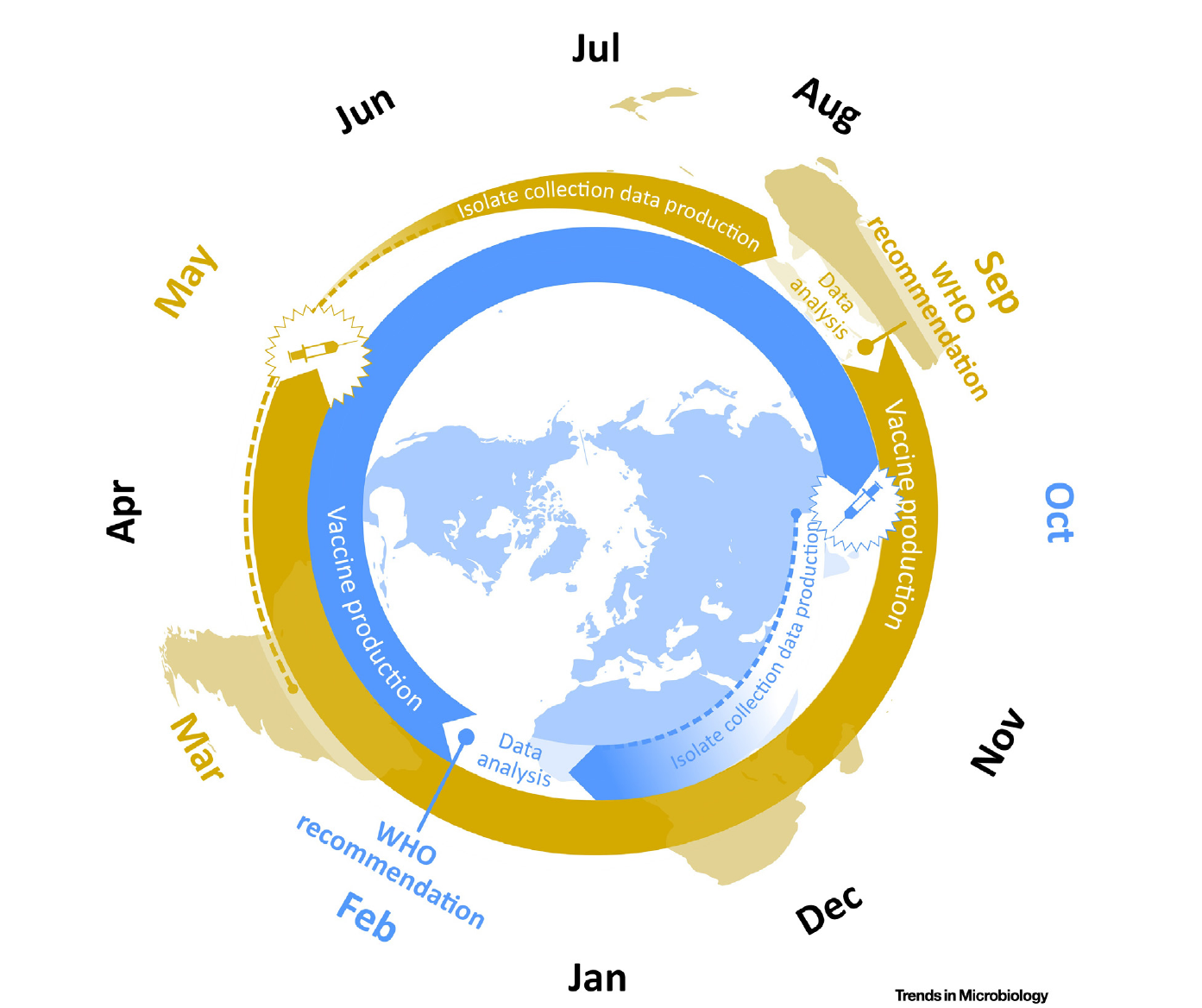Klingen and McHardy, Trends in Microbiology
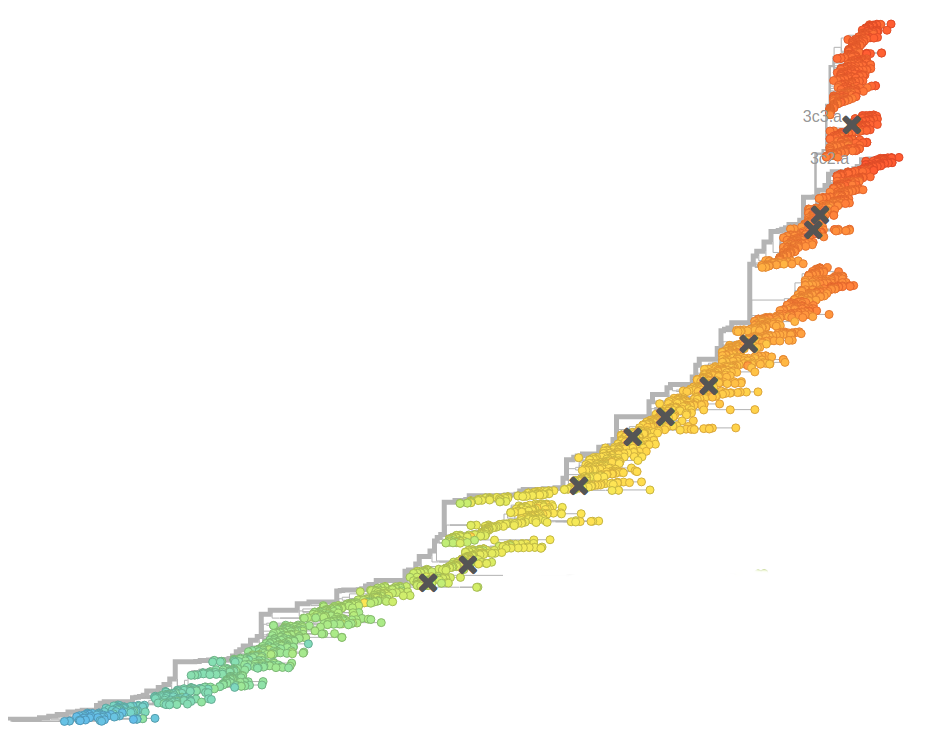
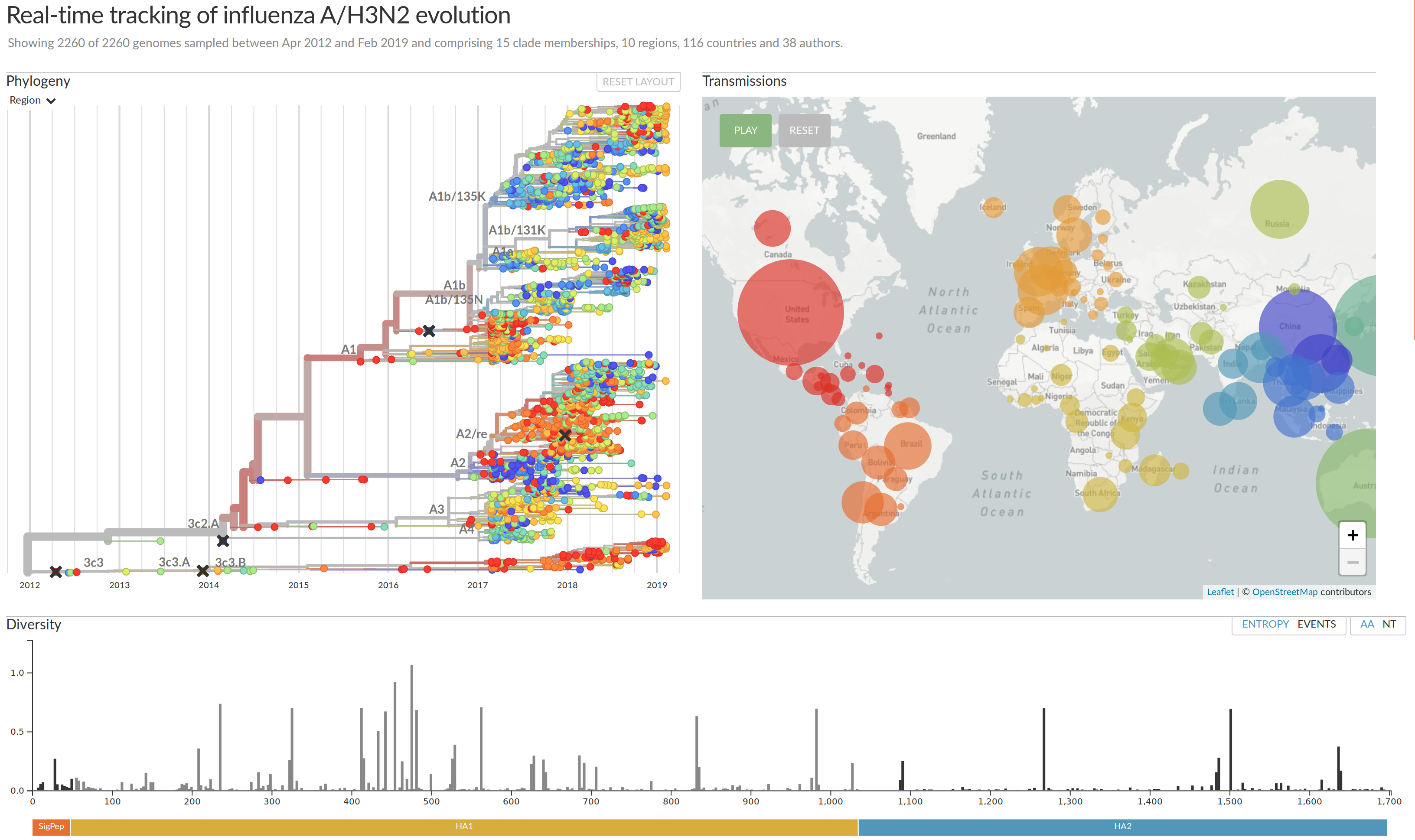
nextflu.org
joint work with Trevor Bedford & his lab
Fitness variation in rapidly adapting populations
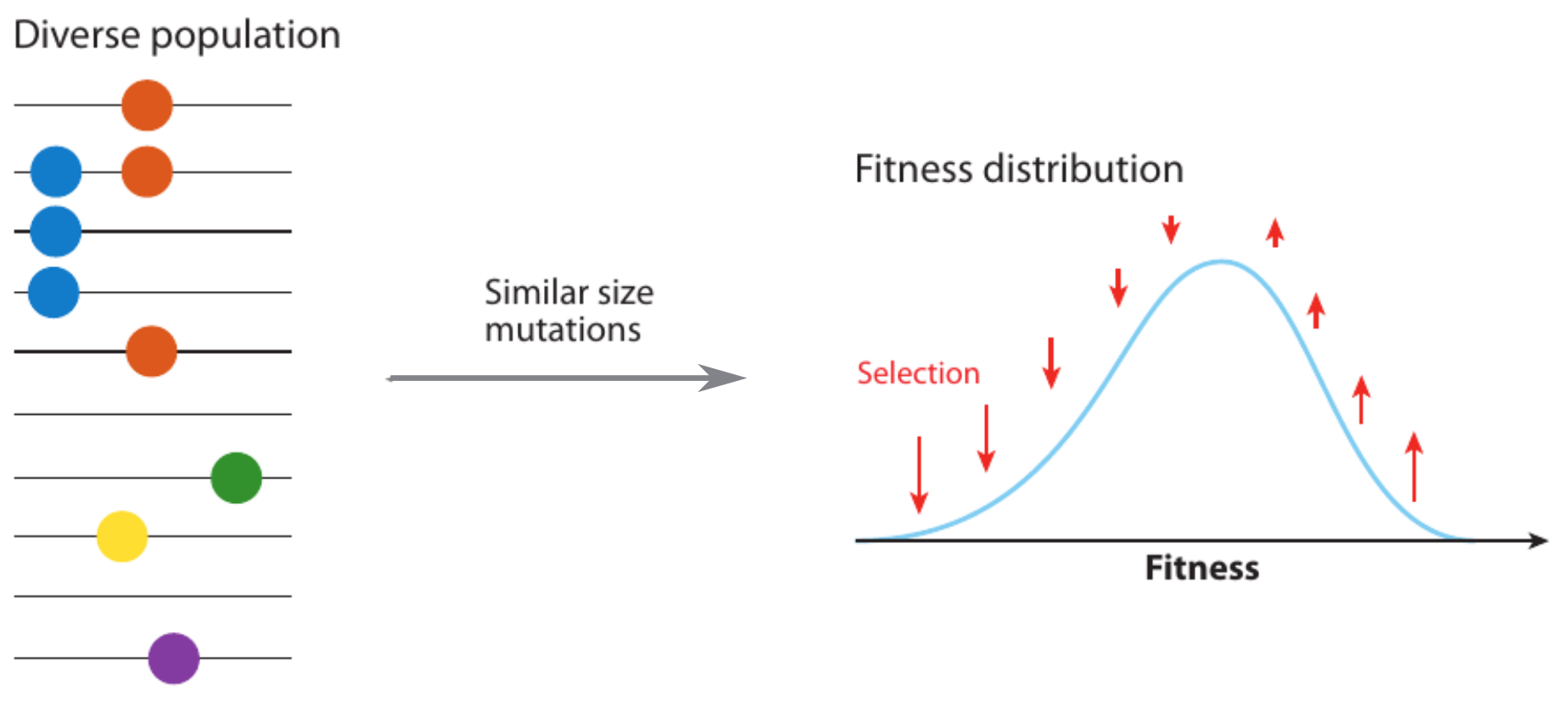
- Speed of adaptation is logarithmic in population size
- Environment (fitness landscape), not mutation supply, determines adaptation
- Different models have universal emerging properties
Neutral/Kingman coalescent
strong selection
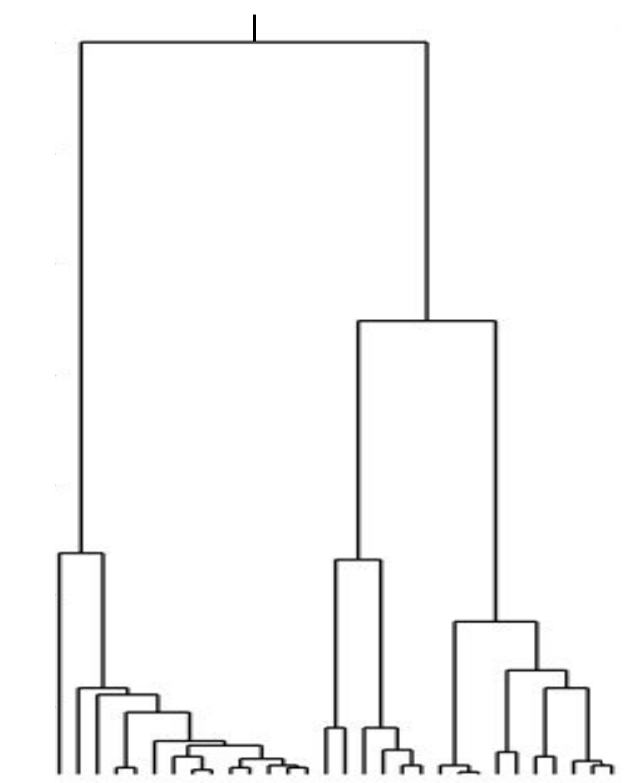
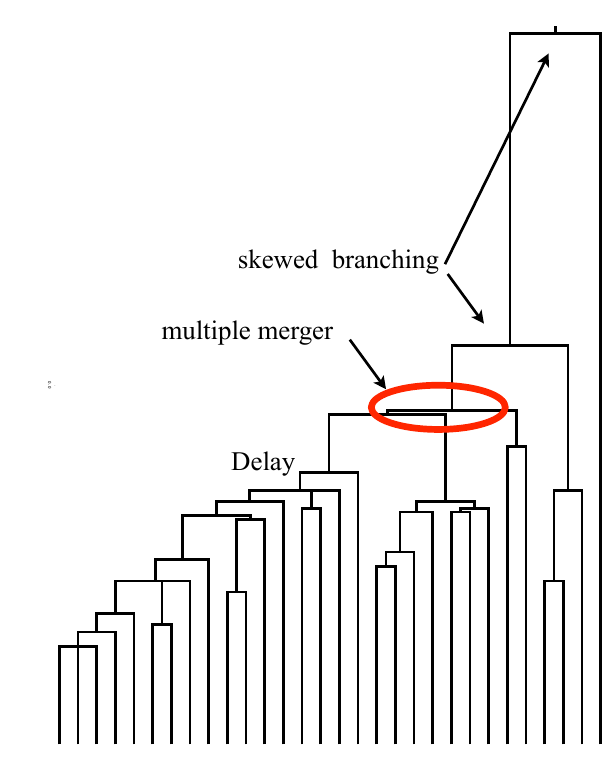
Bolthausen-Sznitman Coalescent
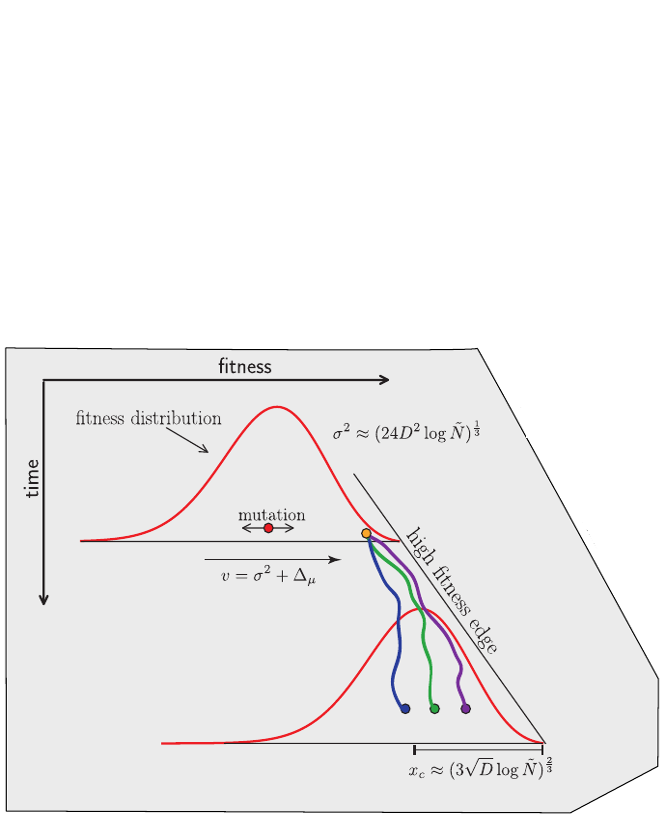
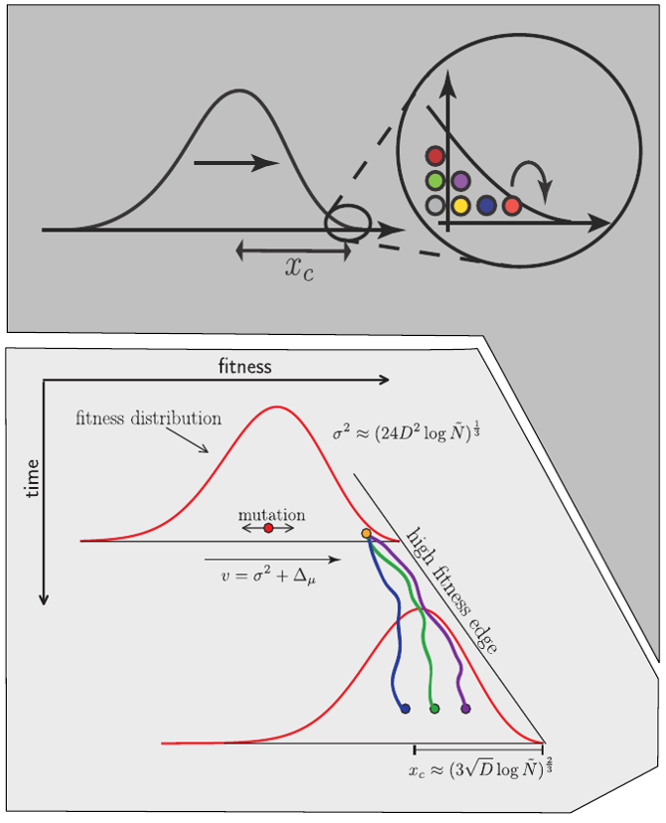
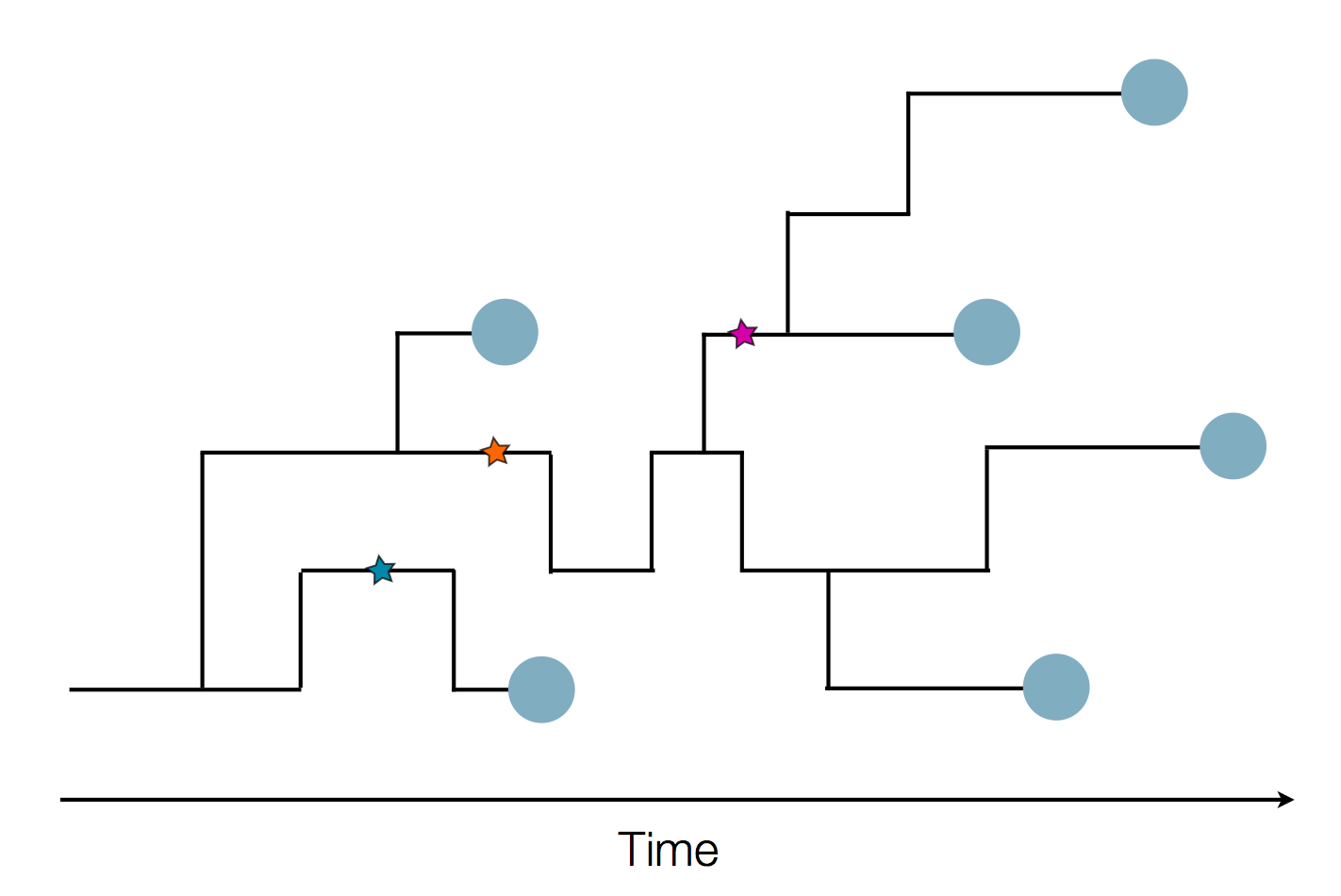
Bursts in a tree ↔ high fitness genotypes
Can we read fitness of a tree?
Predicting evolution
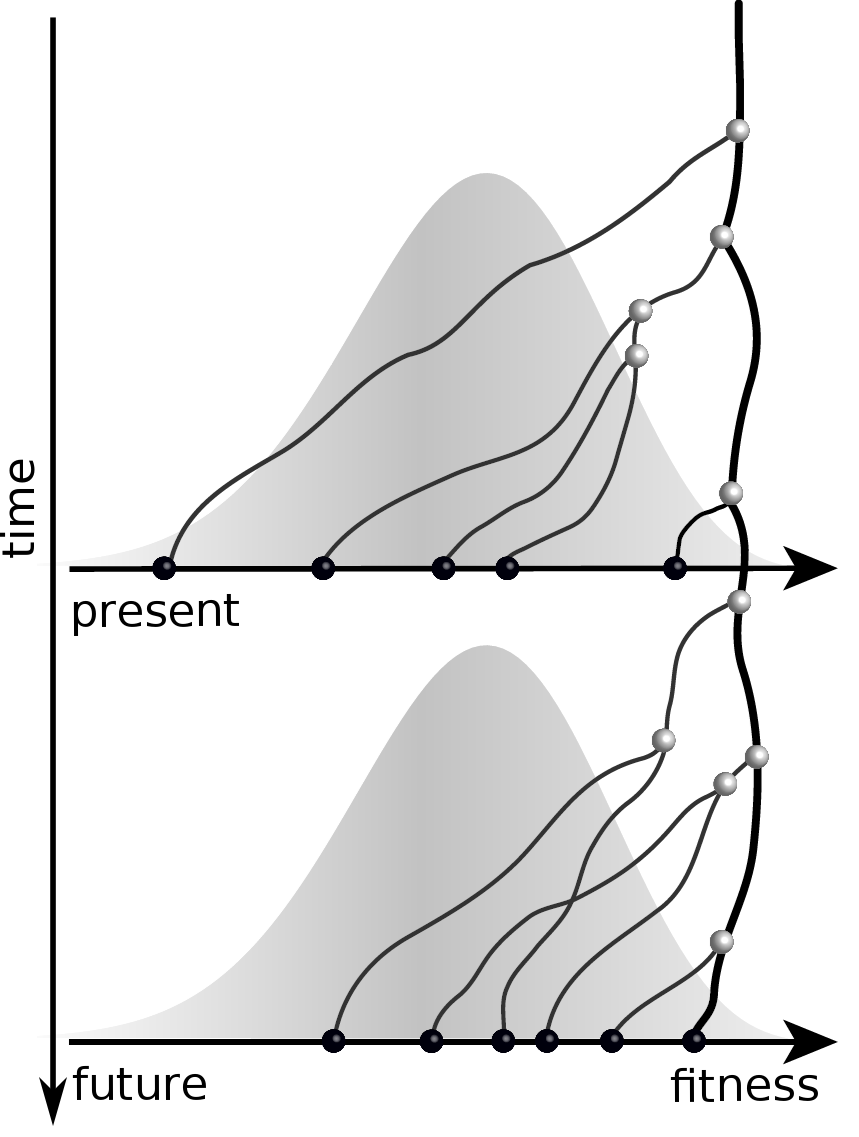
Given the branching pattern:
- can we predict fitness?
- pick the closest relative of the future?
Fitness inference from trees
P(x|T)=1Z(T)p0(x0)nint∏i=0g(xi1,ti1|xi,ti)g(xi2,ti2|xi,ti)
RN, Russell, Shraiman, eLife, 2014
Validate on simulation data
- simulate evolution
- sample sequences
- reconstruct trees
- infer fitness
- predict ancestor of future
- compare to truth
Validation on simulated data
Prediction of the dominating H3N2 influenza strain
- no influenza specific input
- how can the model be improved? (see model by Luksza & Laessig)
- what other context might this apply?
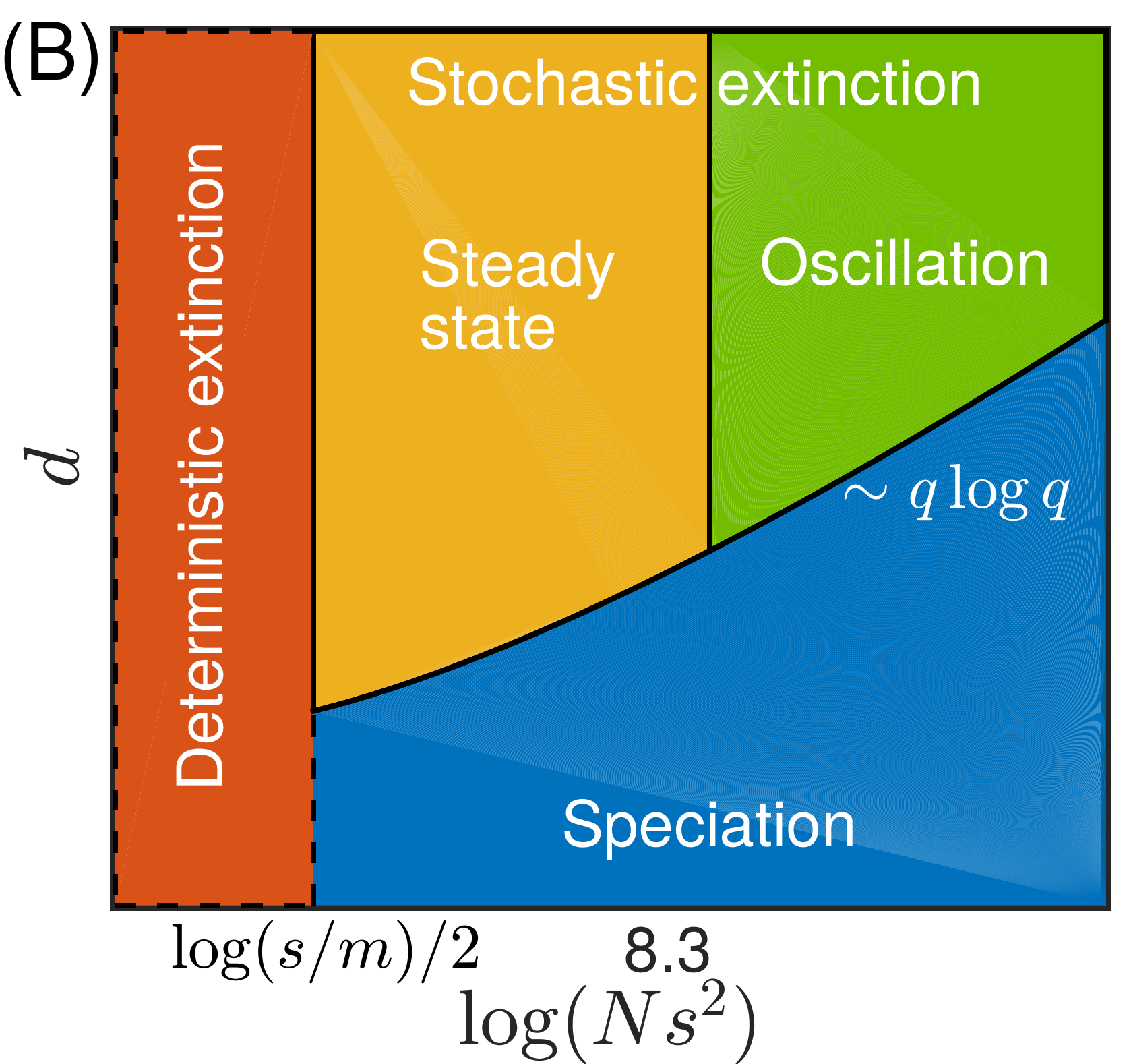
There are many ways to escape immunity -- why doesn't influenza speciate?
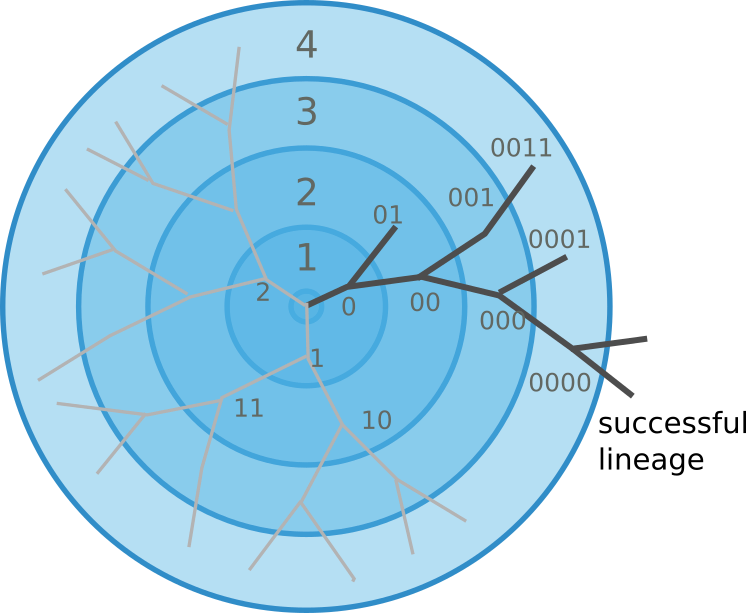
There are many ways to escape immunity -- why doesn't influenza speciate?
Combining SIR-models and rapid molecular adaptation
- Infections with strain a: dIadt=βSaIa−(ν+γ)Ia
- Susceptibility to strain a: Sa=e−∑bKabRb
- Recovered from stain a: dRadt=νIa−γRa
- Cross-immunity: Kab=e−|a−b|d
- Mutations from a→b reduce cross-immunity and increase susceptibility
- Antigenic evolution is essential to establish seasonal patterns
Transition from pandemic to seasonal patterns
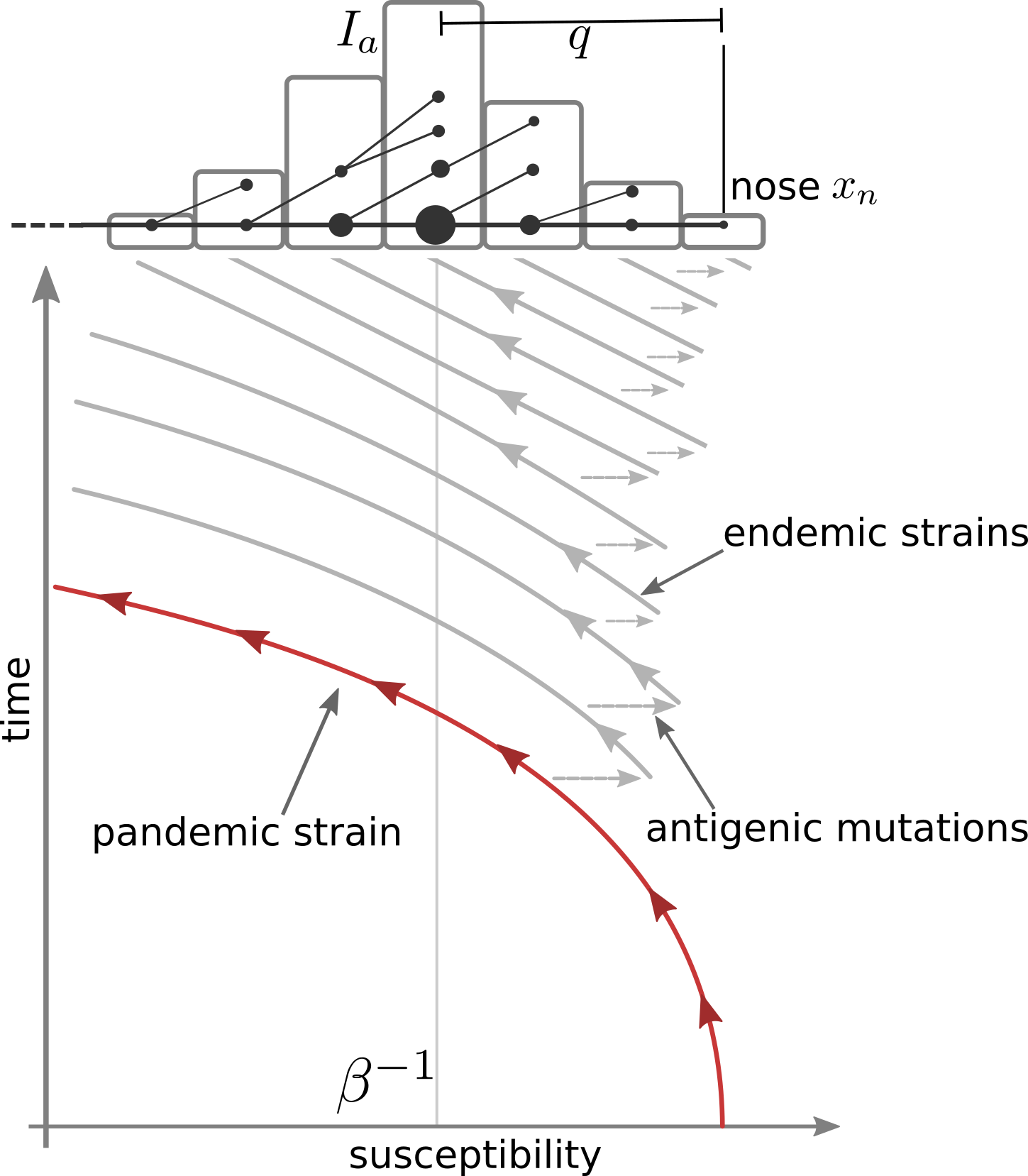
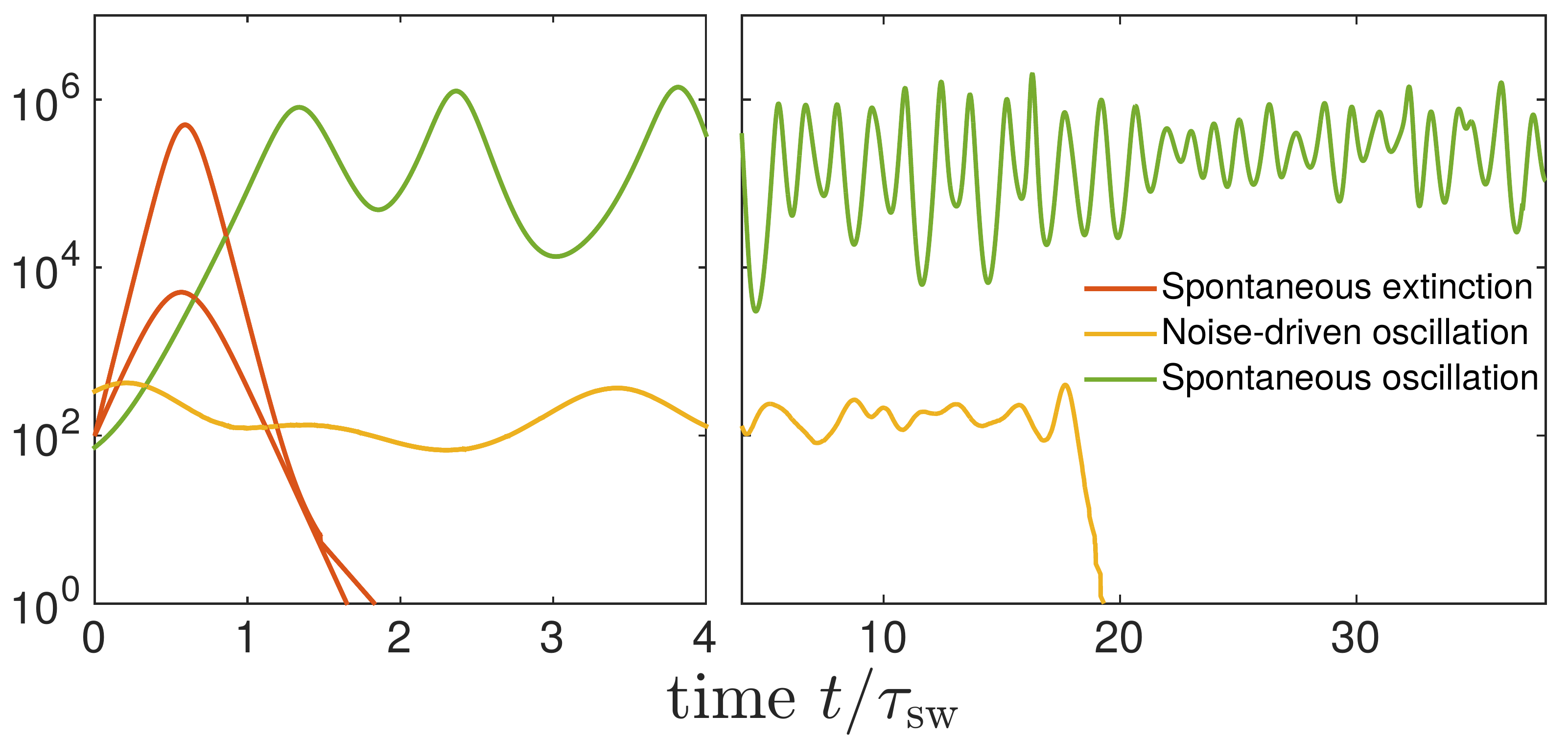
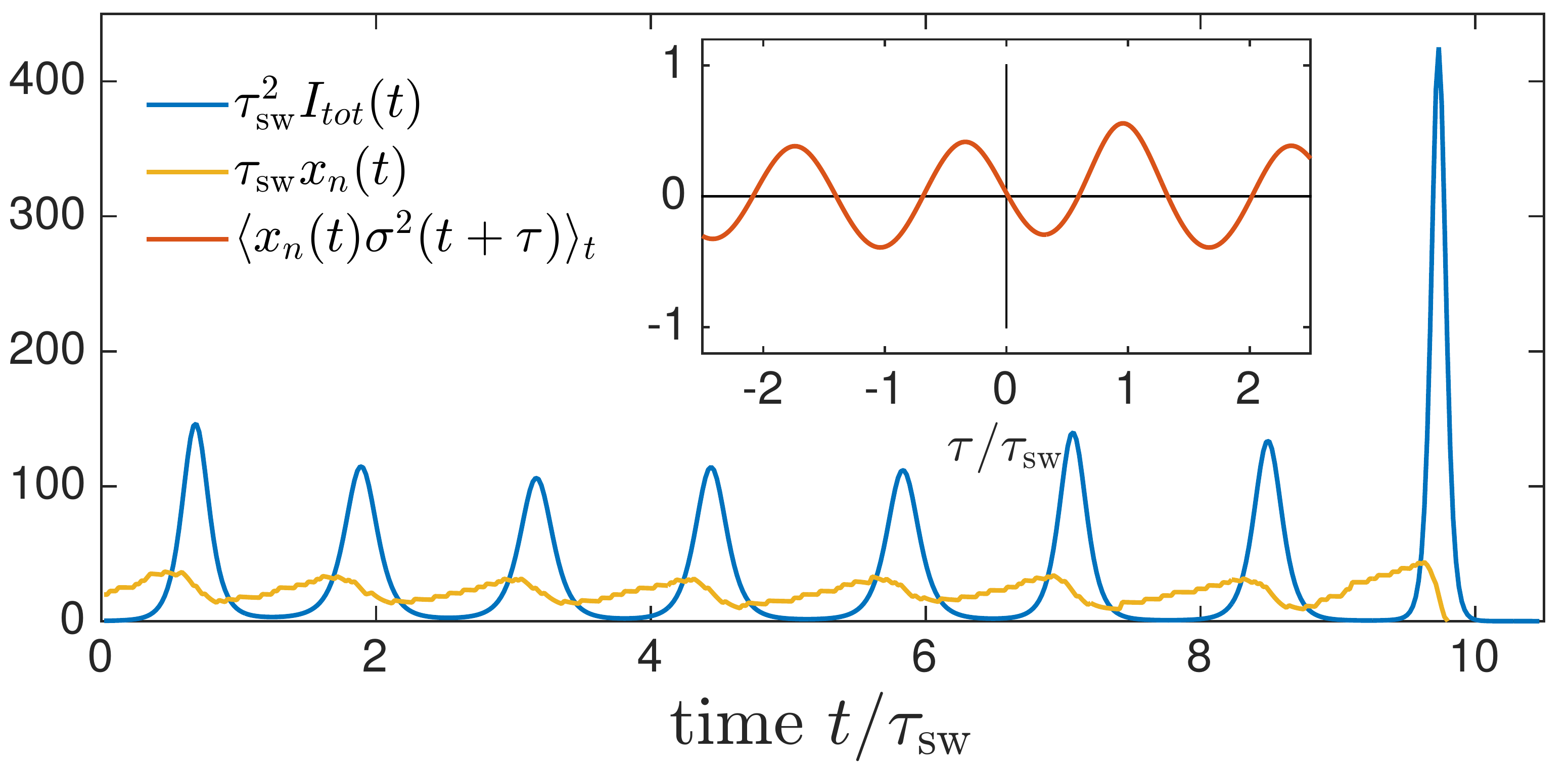
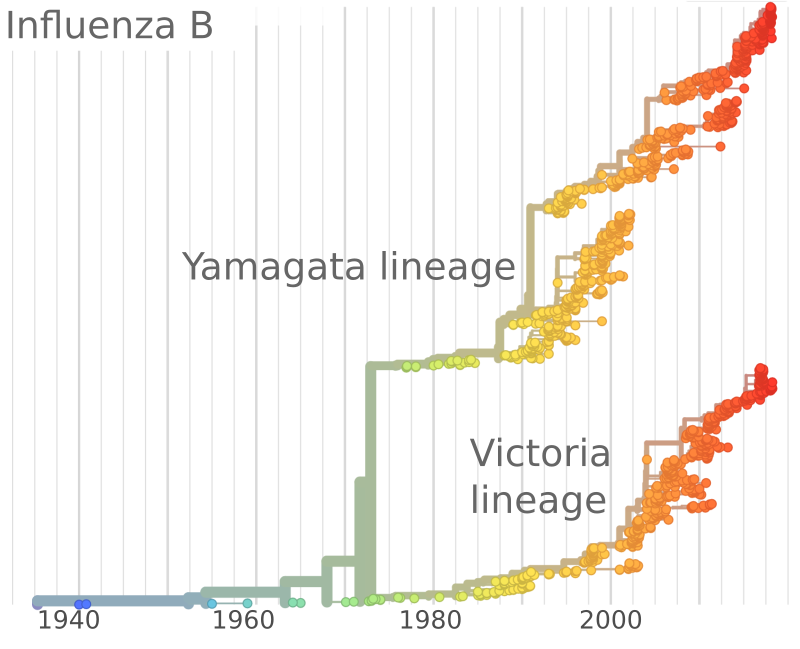
Speciation into antigenically distinct lineages
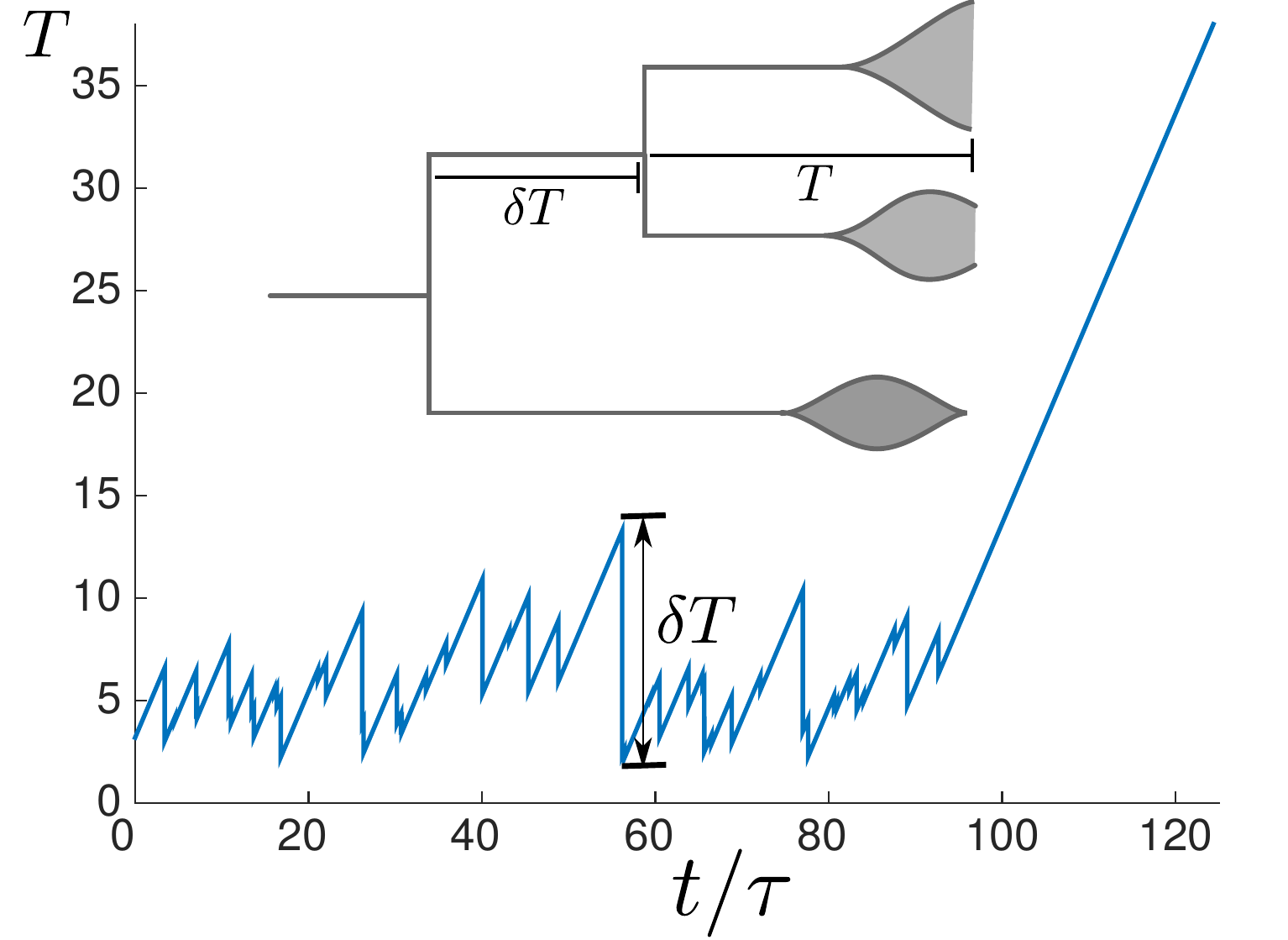
Summary
- RNA virus evolution can be observed directly
- Rapidly adapting population require new population genetic models
- Those model can be used to infer fit clades
- Future influenza population can be anticipated
- Automated real-time analysis can help fight the spread of disease
- Combining epidemiological and population genetic models can explain flu phylogenies
Influenza and Theory acknowledgments
- Le Yan
- Boris Shraiman
- Colin Russell
- Trevor Bedford
- Oskar Hallatschek
Acknowledgments -- nextstrain
- Trevor Bedford
- Colin Megill
- Pavel Sagulenko
- Sidney Bell
- James Hadfield
- Wei Ding
- Emma Hodcroft
- Sanda Dejanic
- John Huddleston
- Barney Potter
RNA virus evolution and the predictability of next year's flu
Richard Neher
Biozentrum, University of Basel
slides at neherlab.org/201903_APS.html