Population genetics of rapid adaptation and fitness inference from trees


Richard Neher
Biozentrum, University of Basel


slides at neherlab.org/201905_phyloseminar.html

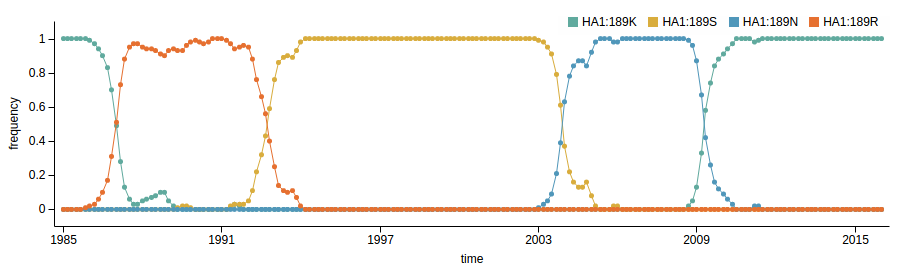
Dynamics, genetic diversity, and phylogenetic trees

evolutionary processes ↔ trees ↔ genetic diversity

Neutral models

  • all individuals are identical → same offspring distribution
  • Kingman coalesence emerges as universal description
  • everything is easy to calculate
  • generalization to structured coalescent
  • generalization to multiple fitness classes possible
    → background selection

But: completely unsuitable to treat adaptive evolution!

Neutral/Kingman coalescent

strong selection

RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007; Desai, Walczak, Fisher, Genetics, 2013

Fitness variation in rapidly adapting populations

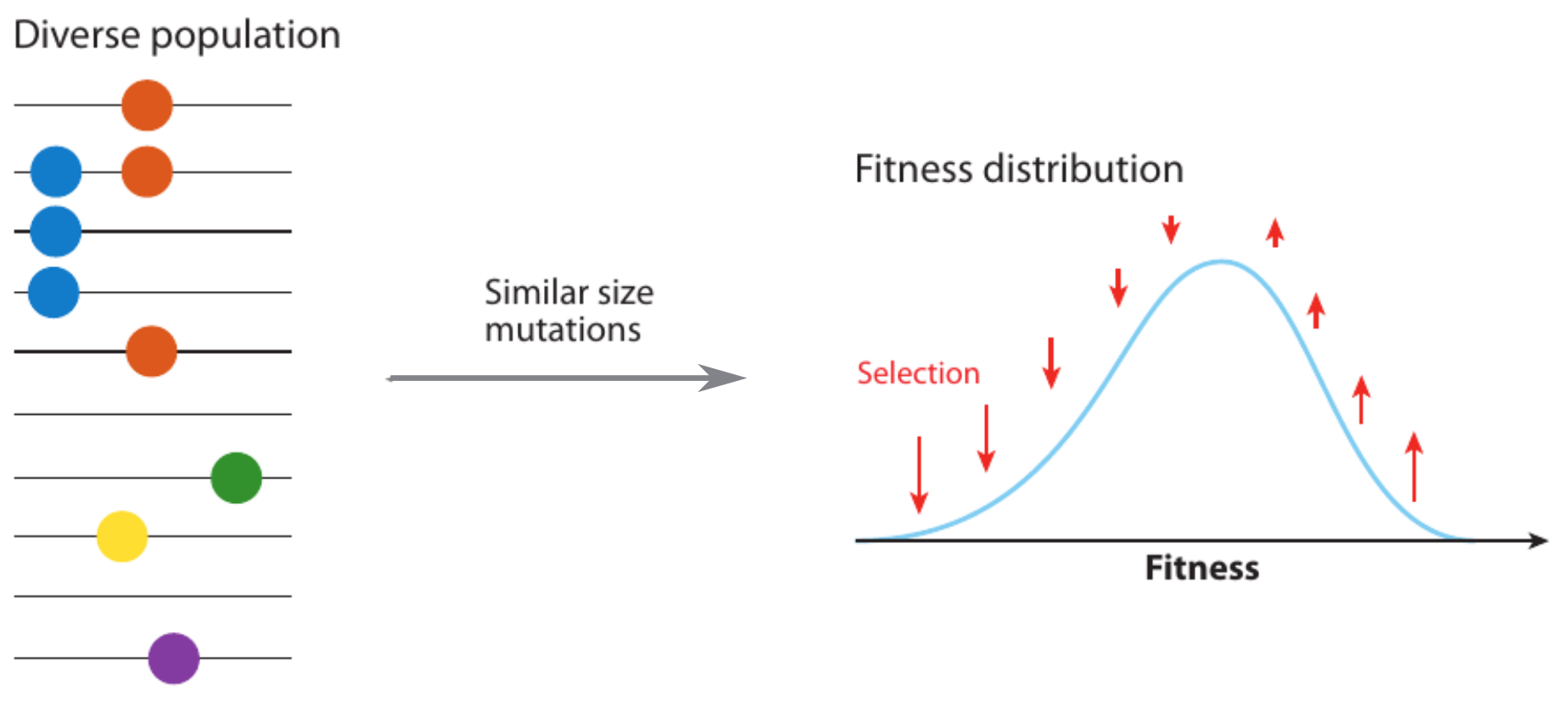
RN, Annual Reviews, 2013; Desai & Fisher; Brunet & Derride; Kessler & Levine

Traveling wave models of adaptation

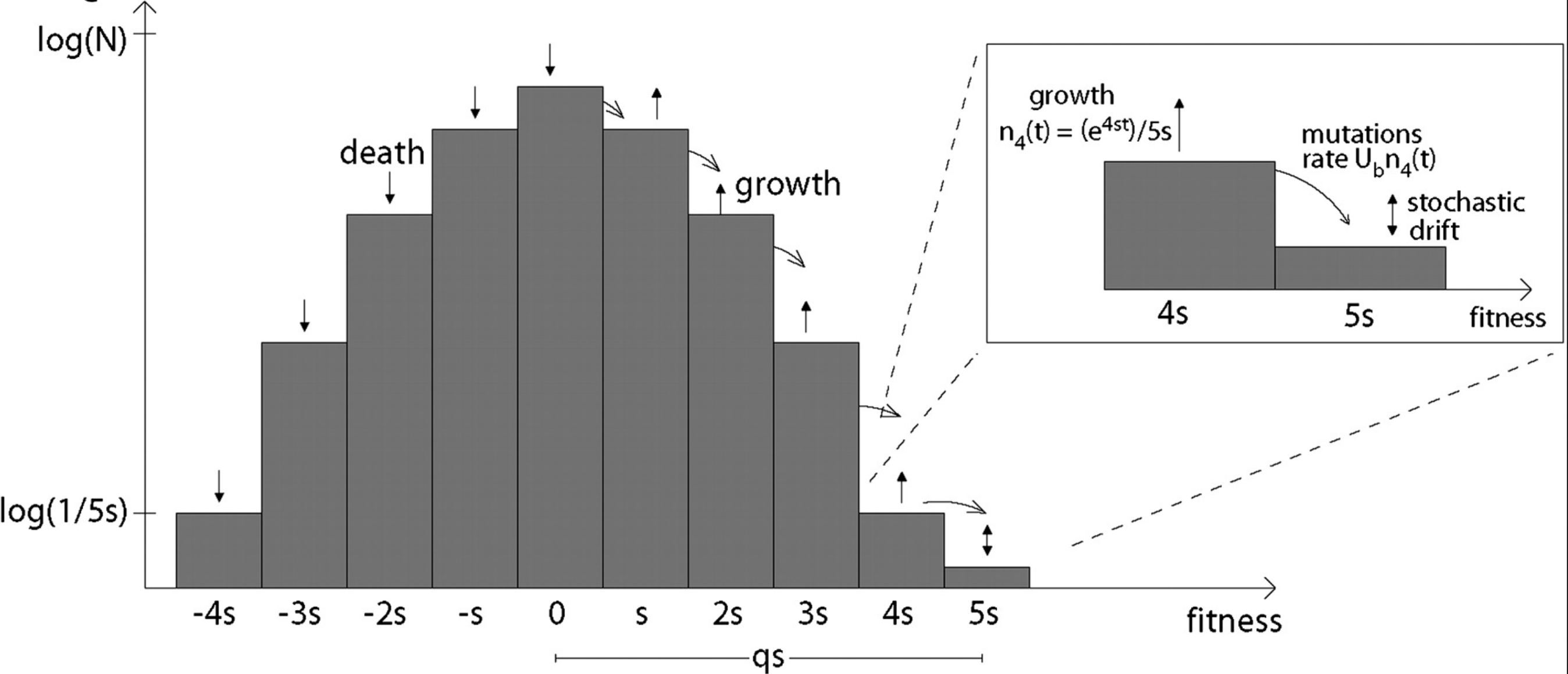
  • Speed of adaptation is logarithmic in population size
  • Environment (fitness landscape), not mutation supply, determines adaptation
  • Different models have universal emerging properties
Desai & Fisher, Genetics

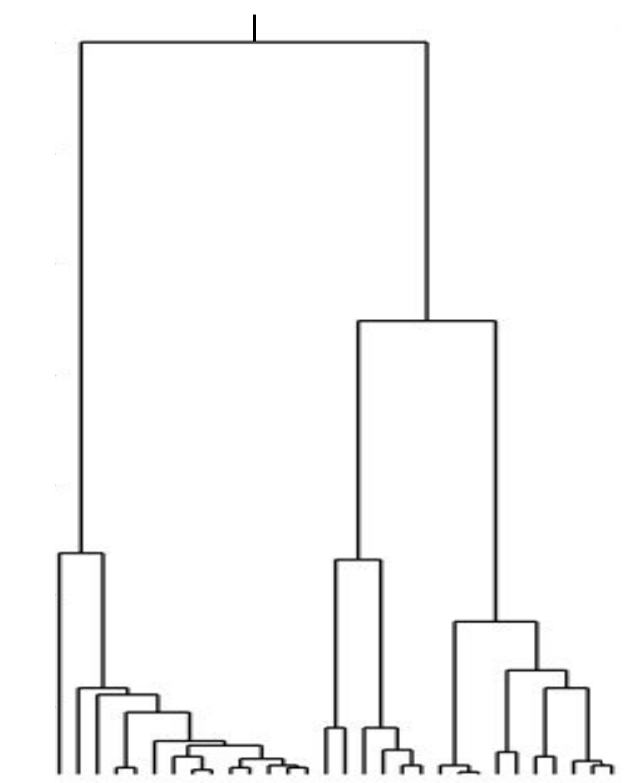
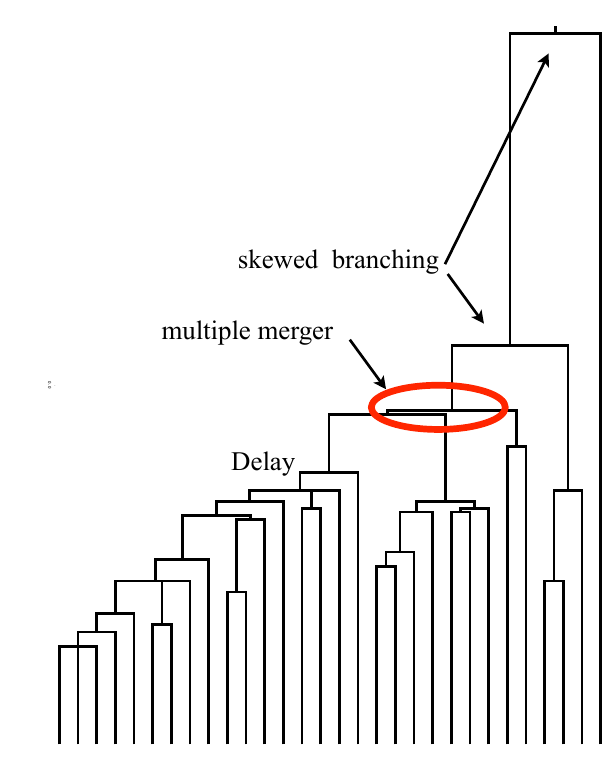
Bolthausen-Sznitman Coalescent

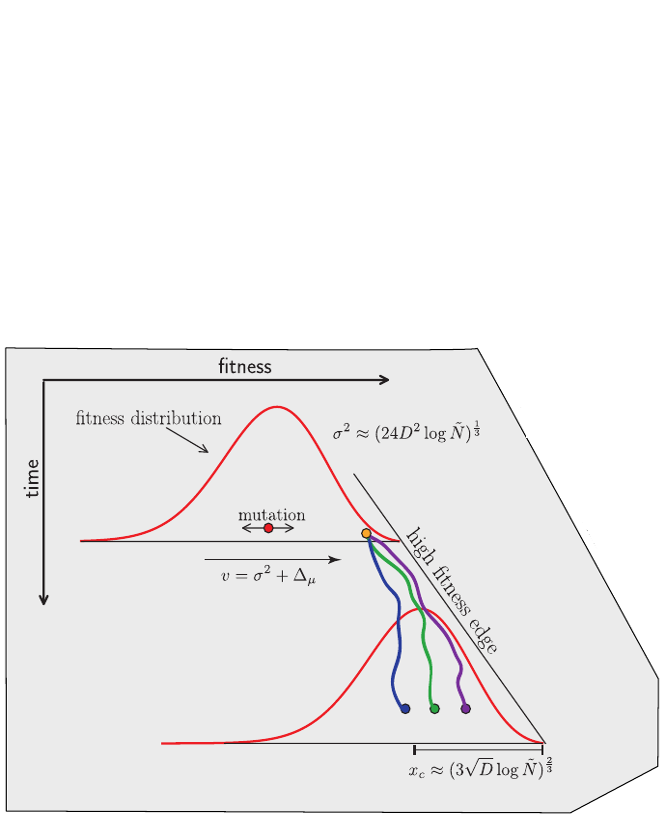
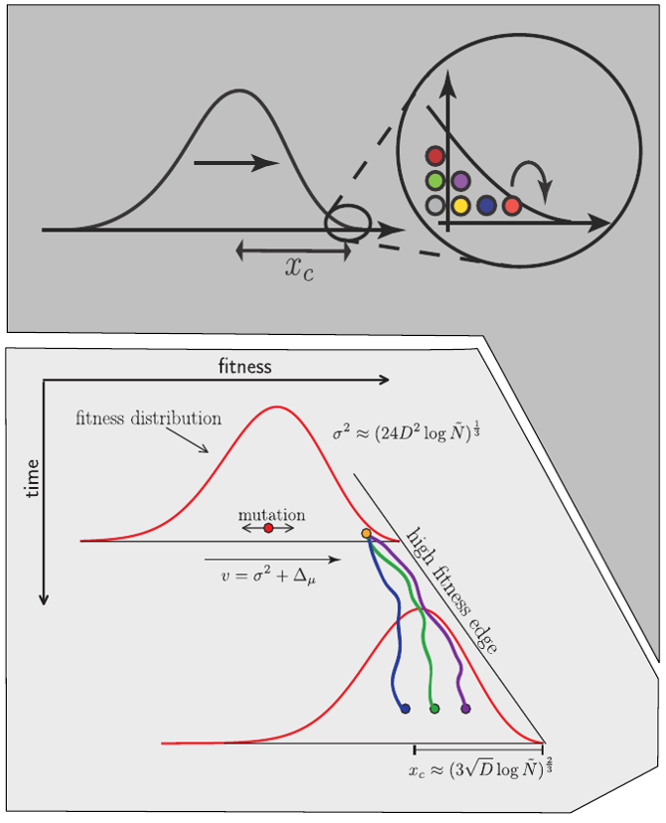
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007; Desai, Walczak, Fisher, Genetics, 2013

Traveling waves and the Bolthausen-Snitman coalescent

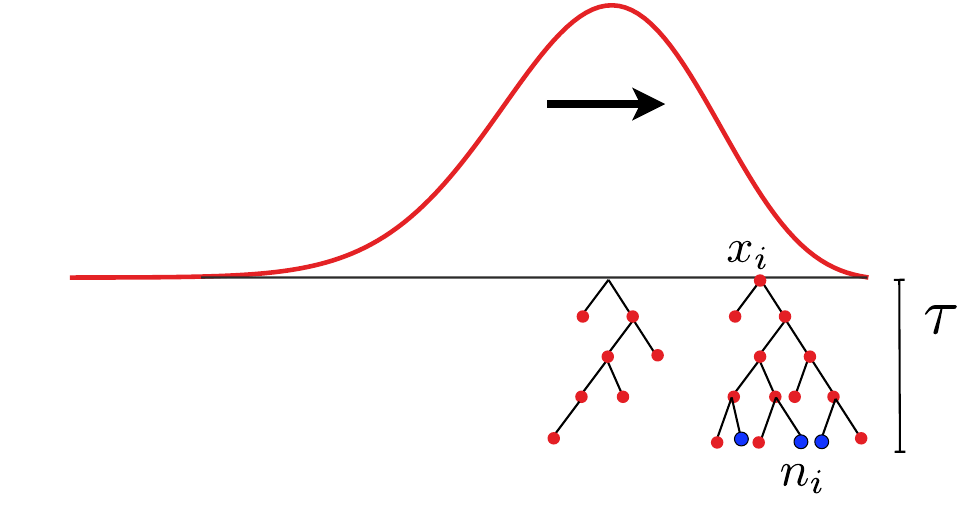
  • Branching process approximation: $P(n_i, t|x_i)$
  • Does a sample (blue dots) have a common ancestor $\tau$ generations ago? $\quad Q_b = \langle \sum_i \left(\frac{n_i}{\sum_j n_j}\right)^b\rangle \approx \frac{\tau-T_c}{T_c(b-1)} $
  • Non-exchangeable at short times: fitness is inherited, lineages grow at different speed
  • On intermediate time scales: exchangeable with power-law tail distribution: $P(n_i) \sim n_i^{-2}$
RN, Hallatschek, PNAS, 2013; see also Brunet and Derrida, PRE, 2007

Universality of the Bolthausen-Sznitman Coalescent (BSC)


  • many small effect mutations → coalescence is BSC like
  • fitness diversity $\sigma$, not population size determines $T_{MRCA}$
  • the time scale of coalescence is always $T_c \sim \sigma^{-1}\sqrt{\log N}$
  • frequency dynamics is not diffusive, but has Levy-flight properties
  • Can be extended to sexual populations
Kosheleva, Desai; Desai, Walczak, Fisher, Genetics, 2013; RN, Hallatschek, PNAS, 2013, RN, Kessinger, Shraiman PNAS, 2013

U-shaped polarized site frequency spectra



RN, Hallatschek, PNAS, 2013

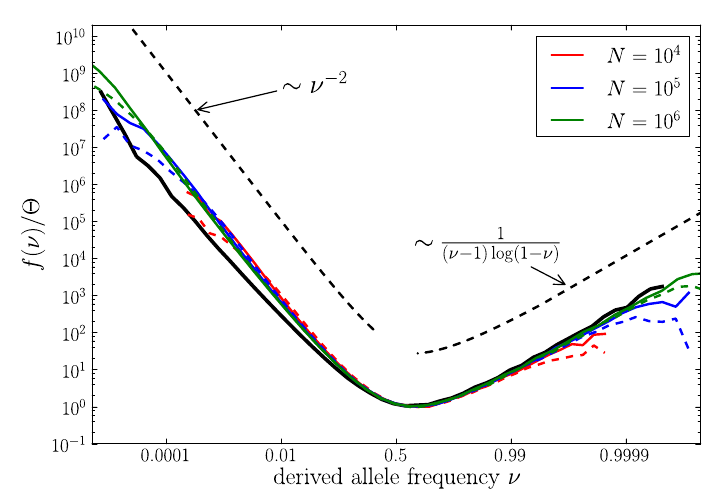
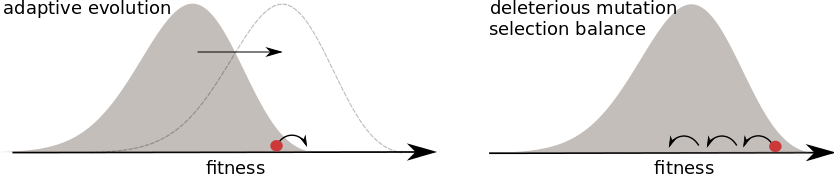
Universality -- adaptation and deleterious mutations




RN, Hallatschek, PNAS, 2013

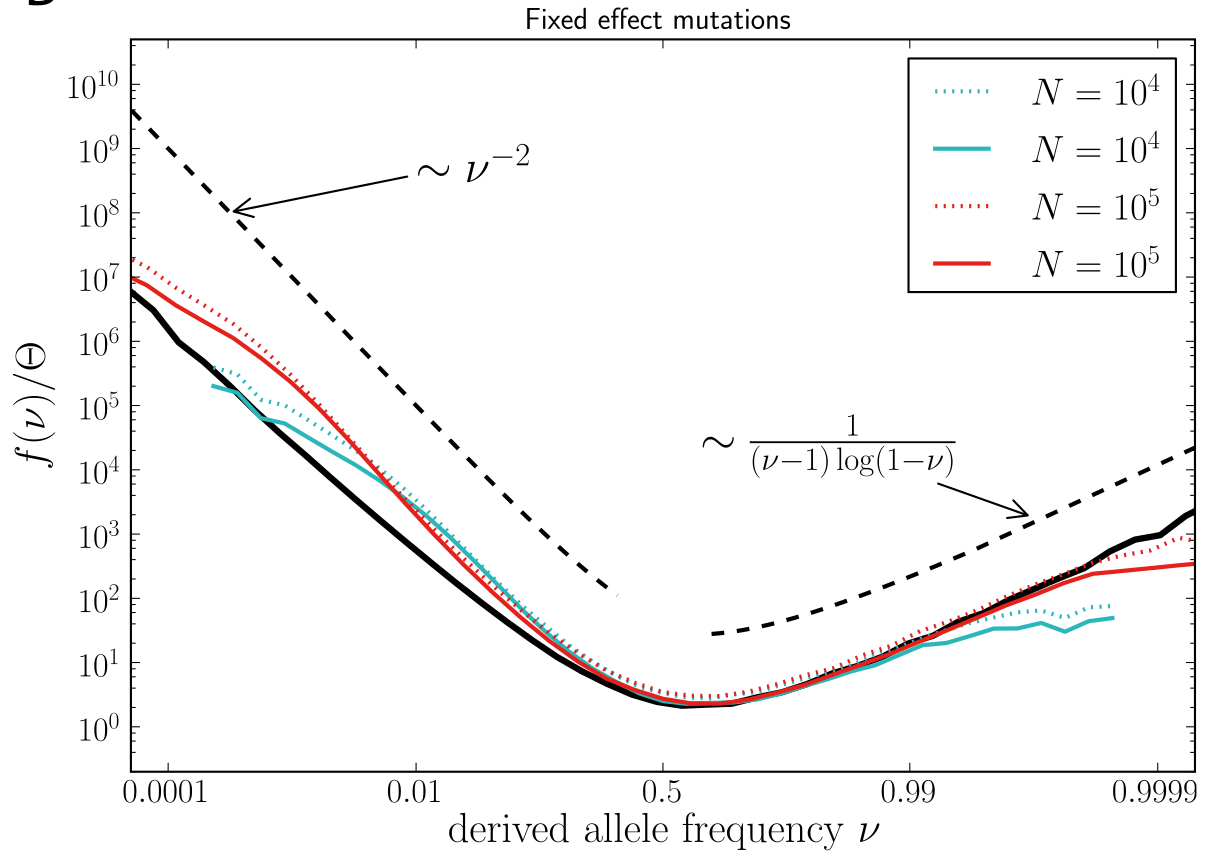
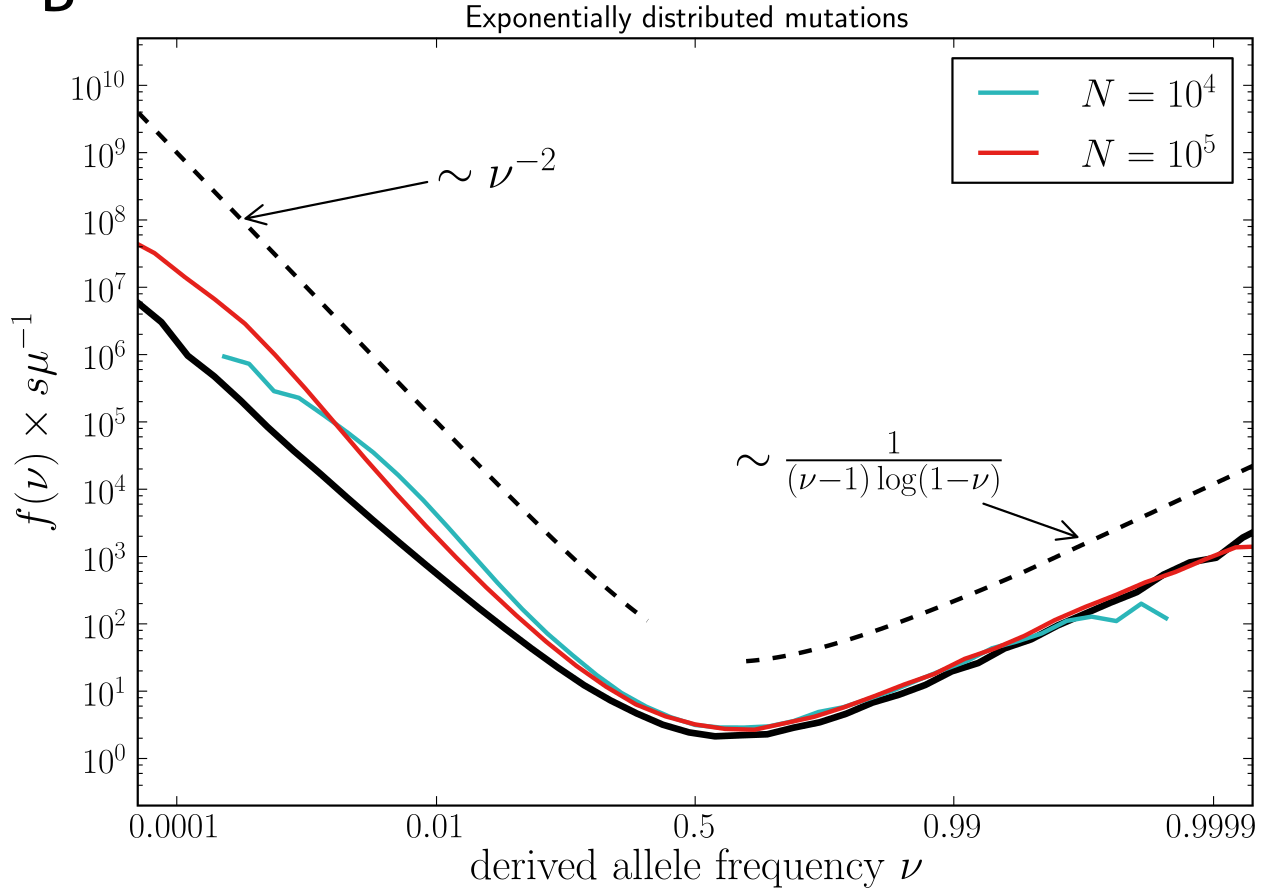
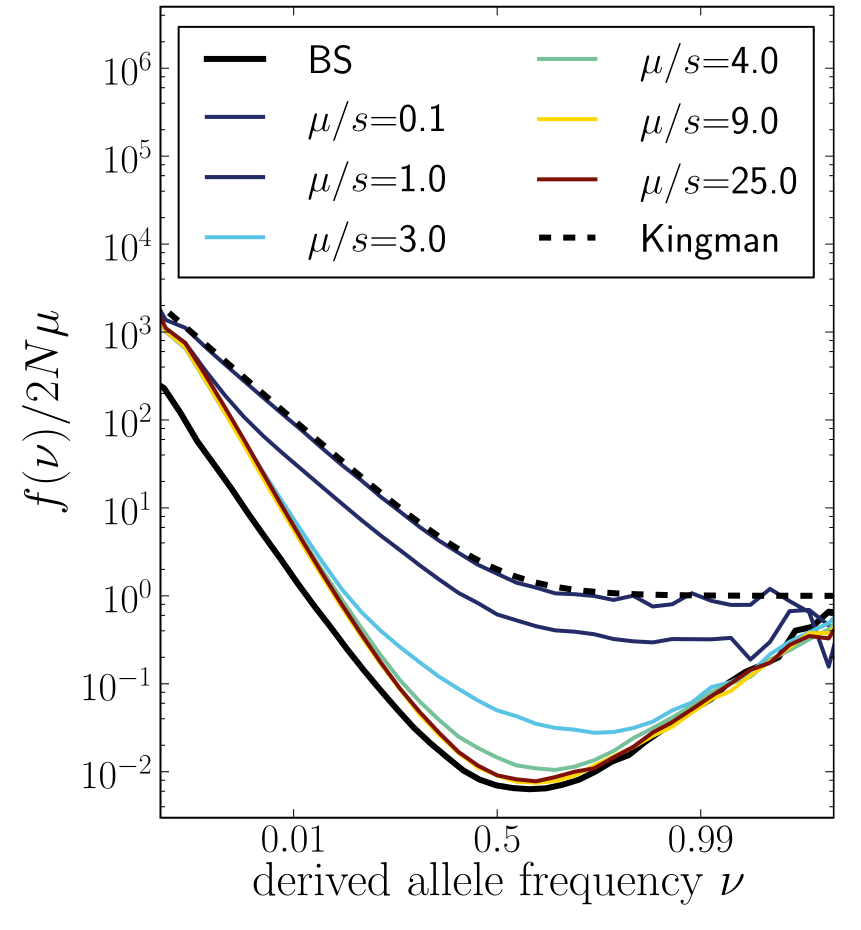
Bursts in a tree ↔ high fitness genotypes

Can we read fitness of a tree?

Predicting evolution

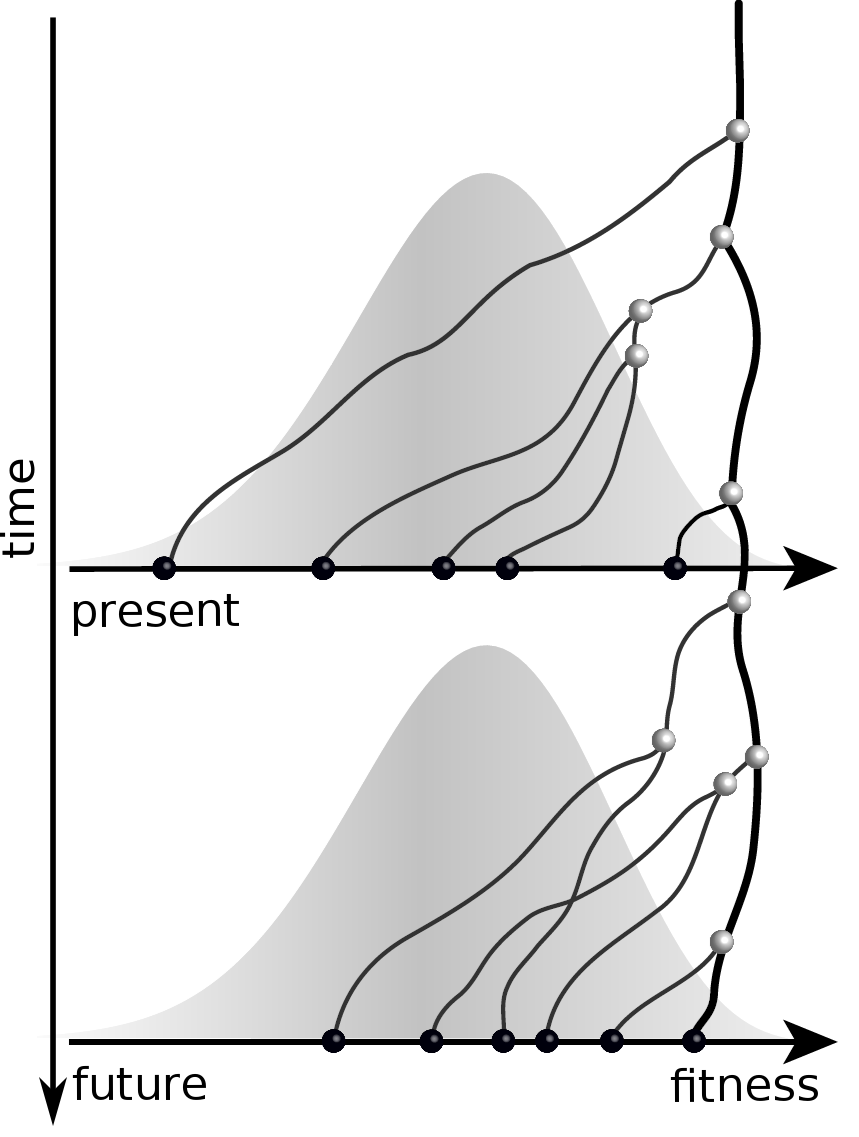
Given the branching pattern:

  • can we predict fitness?
  • pick the closest relative of the future?
RN, Russell, Shraiman, eLife, 2014


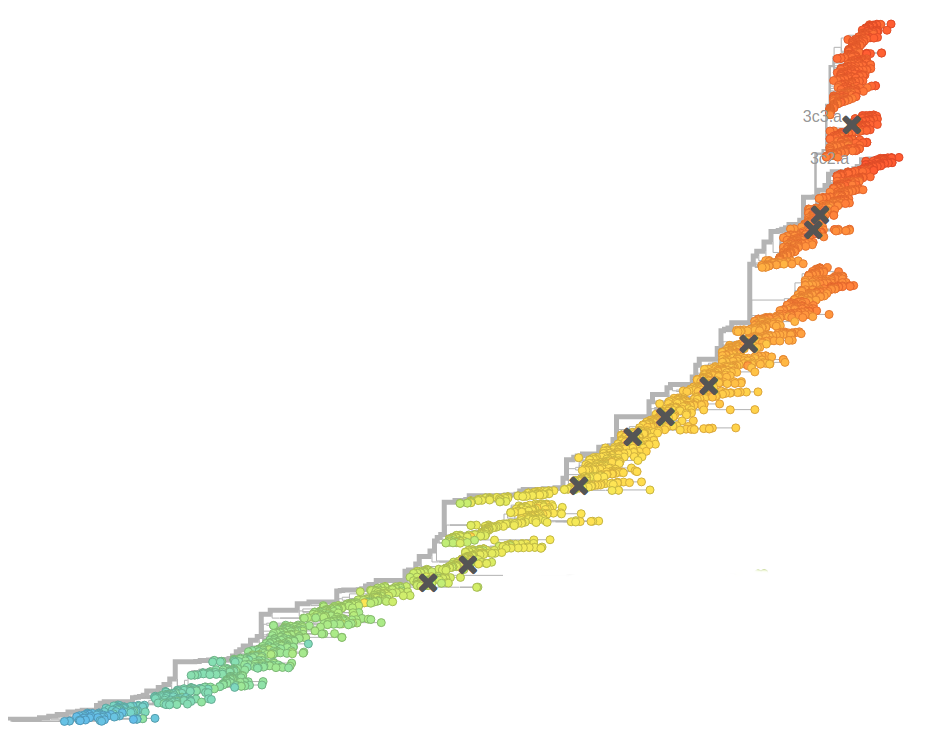
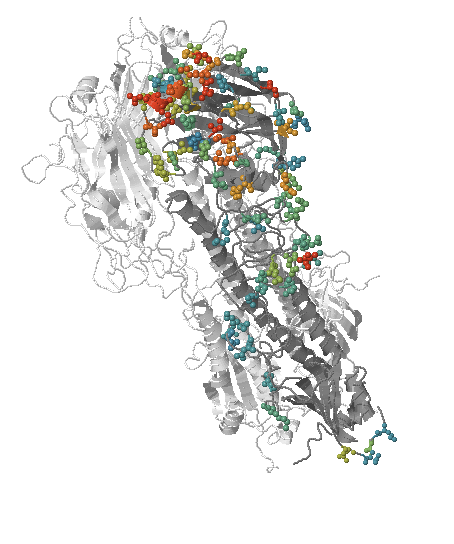
  • Influenza virus evolves to avoid human immunity
  • Vaccines need frequent updates

Fitness inference from trees

$$P(\mathbf{x}|T) = \frac{1}{Z(T)} p_0(x_0) \prod_{i=0}^{n_{int}} g(x_{i_1}, t_{i_1}| x_i, t_i)g(x_{i_2}, t_{i_2}| x_i, t_i)$$

$g(x,t|y,t')$: density of observed child lineages at $(t, x)$ (time,fitness) given a parent at $(t',y)$
conditional no observed branching between parent and child.
RN, Russell, Shraiman, eLife, 2014

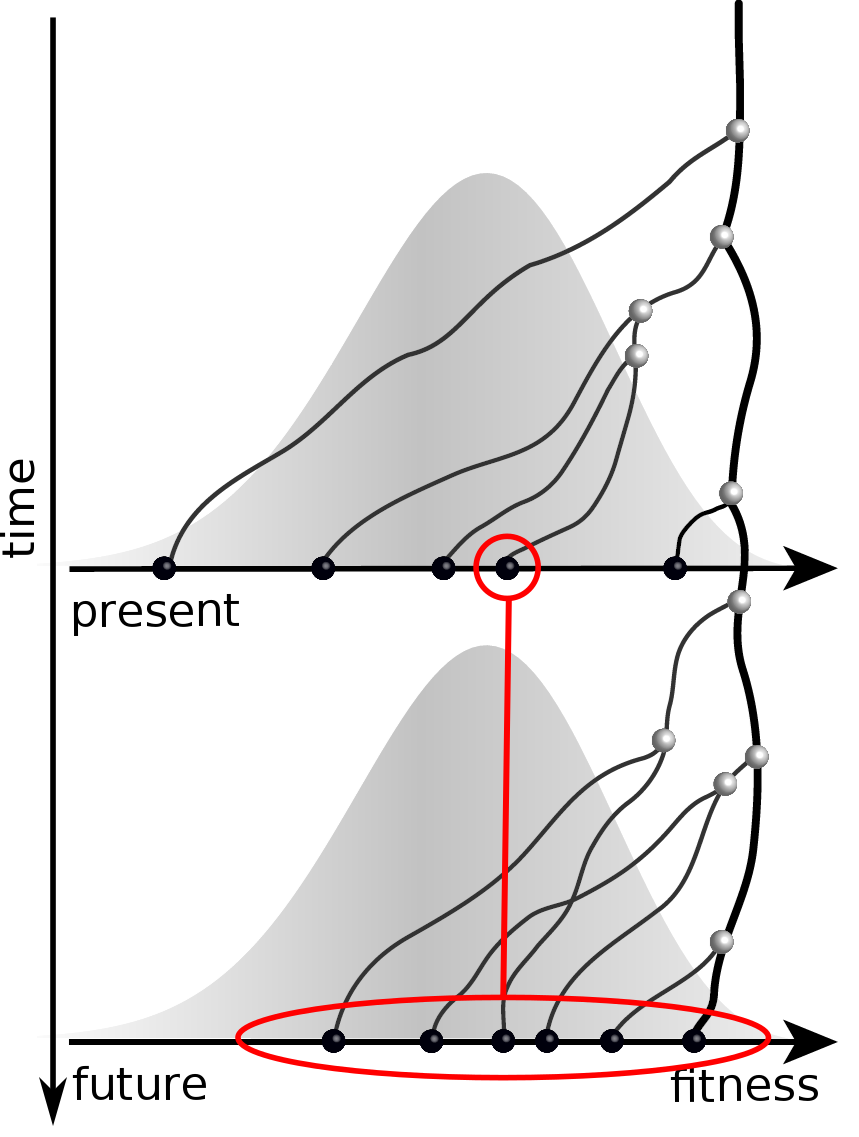
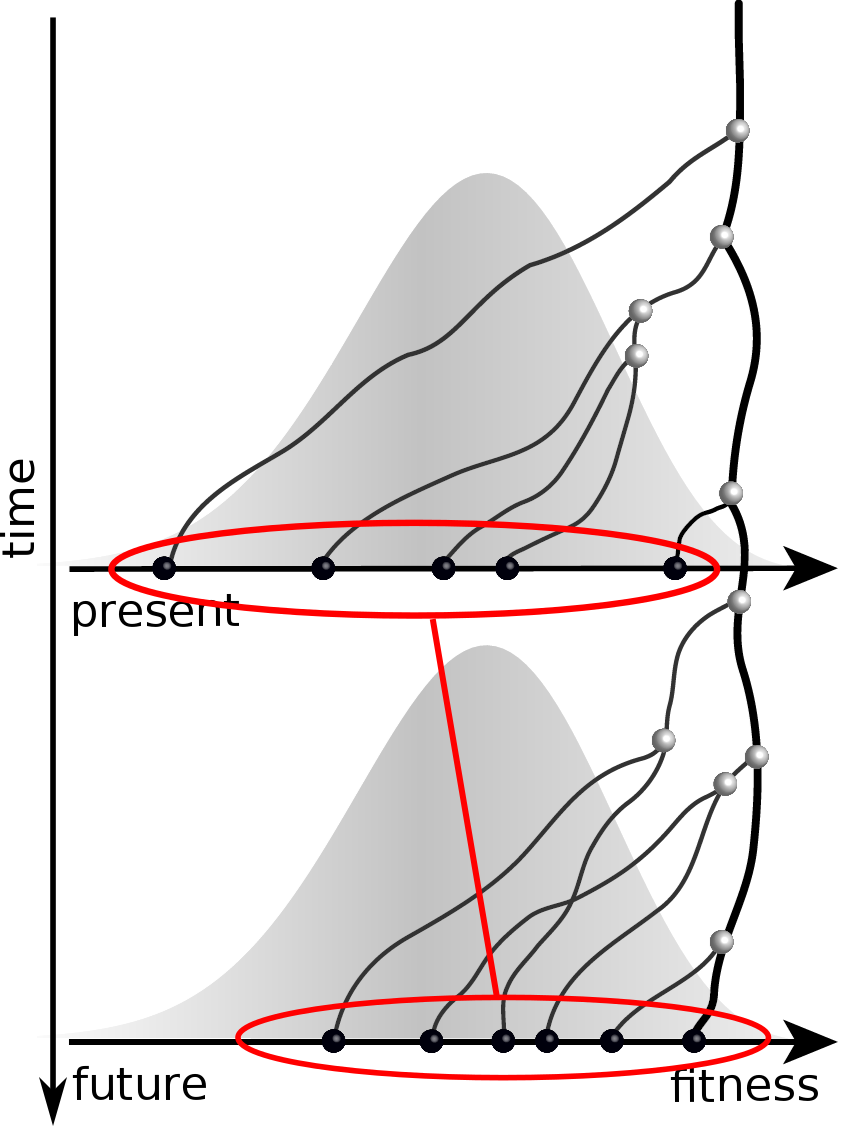
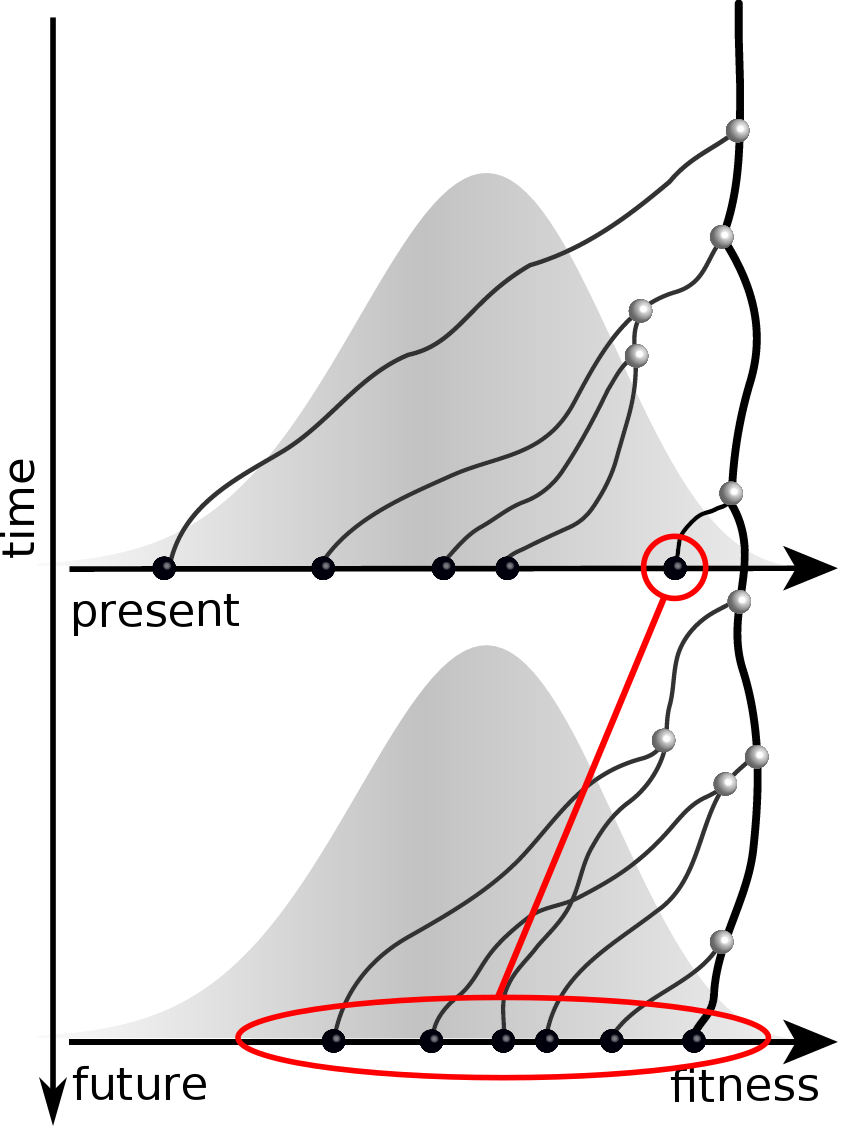
Validate on simulation data

  • simulate evolution
  • sample sequences
  • reconstruct trees
  • infer fitness
  • predict ancestor of future
  • compare to truth
RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Validation on simulated data

RN, Russell, Shraiman, eLife, 2014

Prediction of the dominating H3N2 influenza strain

  • no influenza specific input
  • how can the model be improved? (see model by Luksza & Laessig)
  • what other context might this apply?
 RN, Russell, Shraiman, eLife, 2014

Asymptotic analysis suggested simple heuristic: Local Branching Index

  • For each node, calculate "tree volume" in neighborhood with an exponential kernel
  • Characteristic scale: fraction of the coalescent time scale ($\sim T_c/15$)

Summary

  • Fitness variation → no longer exchangeable pop-gen
  • Mutational dynamics effectively restores exchangeability after some time, but....
  • Resulting offspring distributions have long tails → no longer Kingman
  • Bolthausen-Sznitman coalescent is universal if pioneer strains compete
  • Insights into pop-gen of rapid adaptation → flu prediction

Acknowledgments

  • Boris Shraiman (UCSB)
  • Colin Russell (now Amsterdam)
  • Oskar Hallatschek (UCB)