Tracking and predicting influenza virus diversity
Richard Neher
Biozentrum & SIB, University of Basel
slides at neherlab.org/201910_multistrain.html
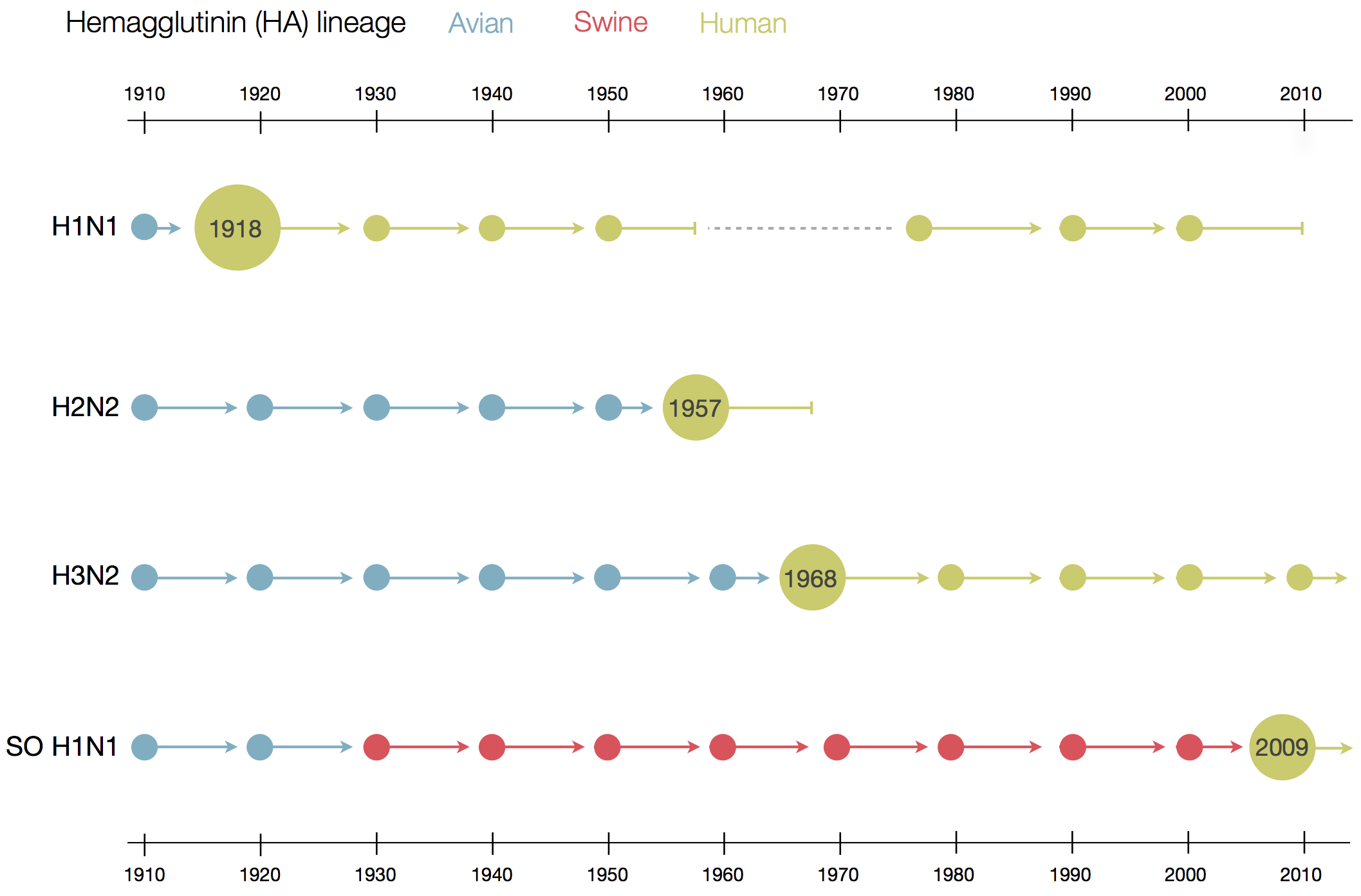
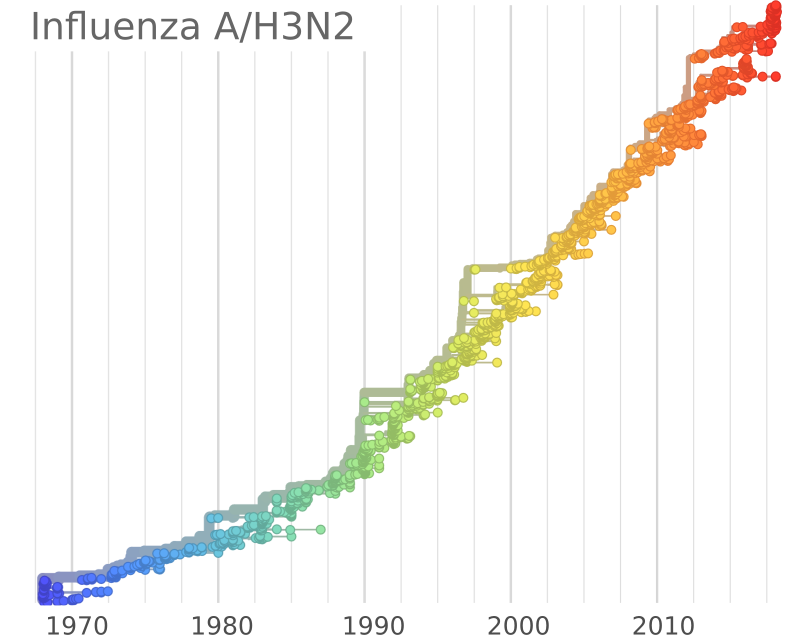
Human seasonal influenza viruses
Positive tests for influenza in the USA by week
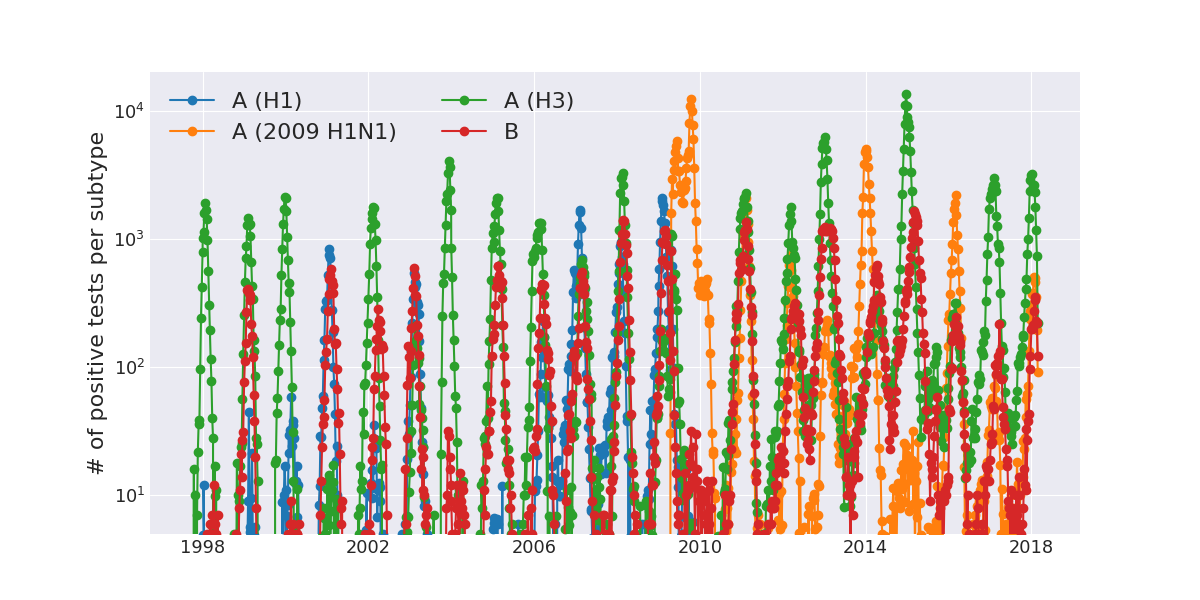Data by the US CDC
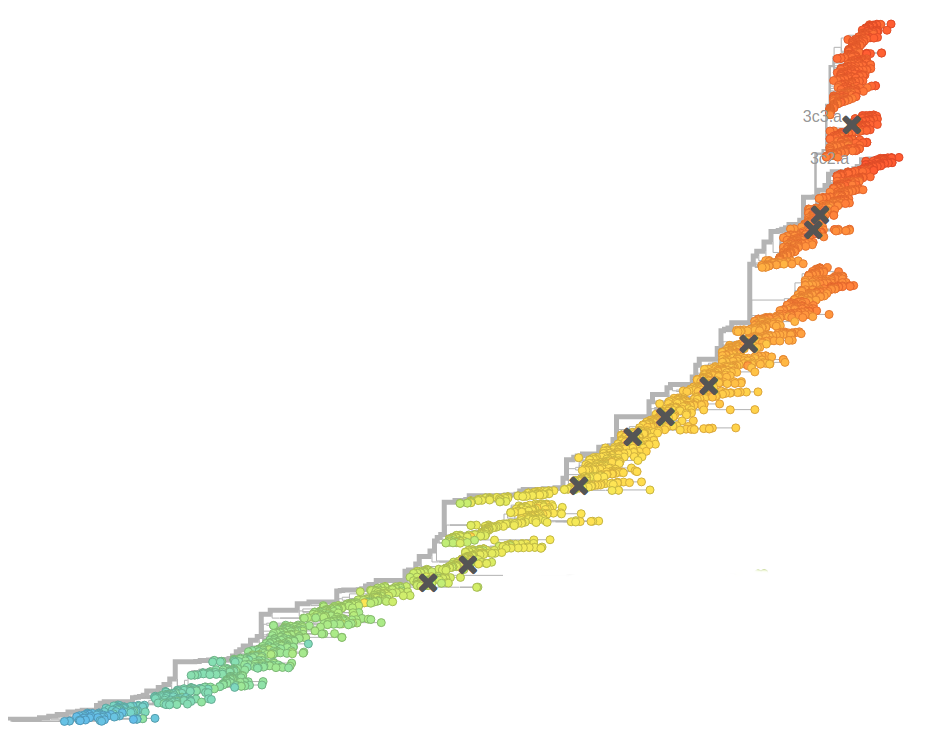
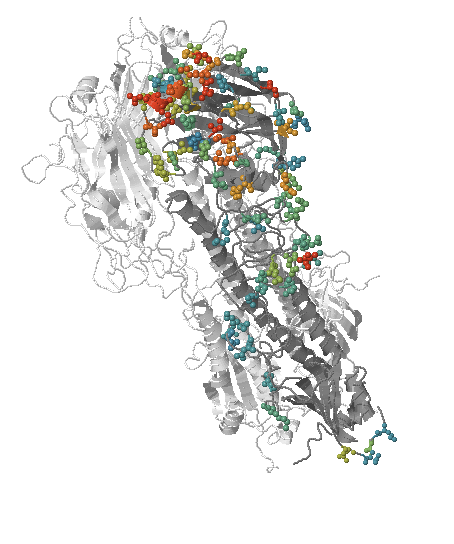
- Influenza viruses evolve to avoid human immunity
- Vaccines need frequent updates
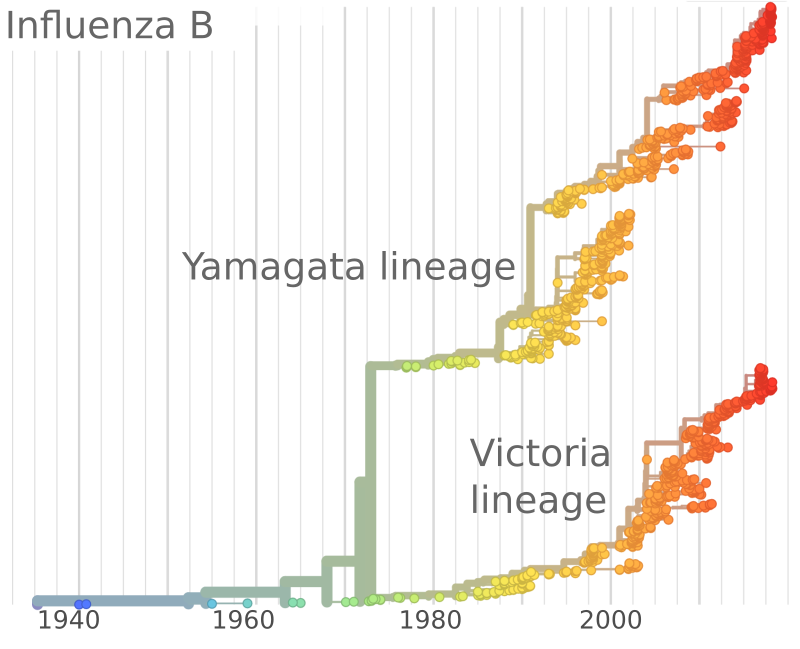
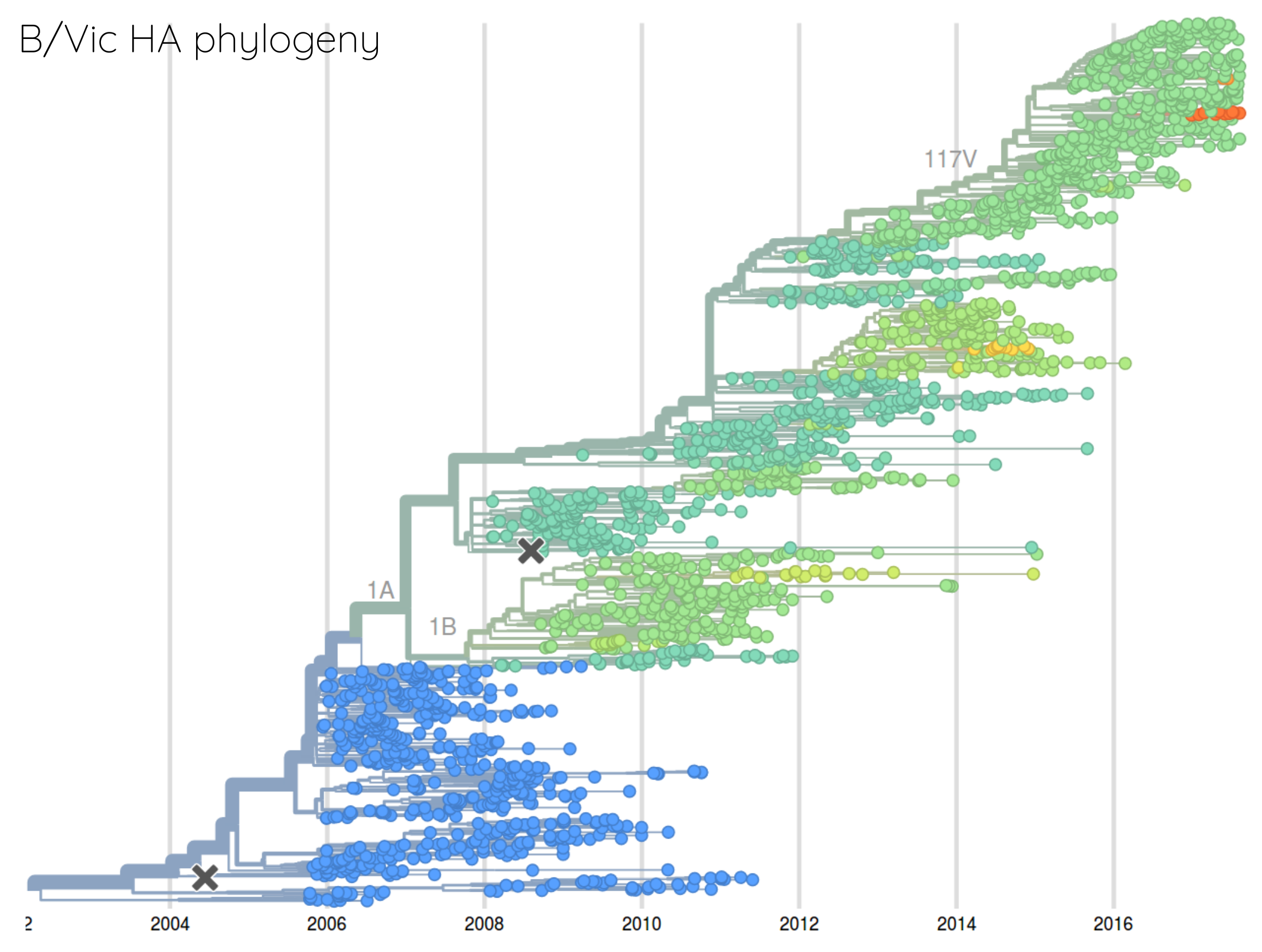
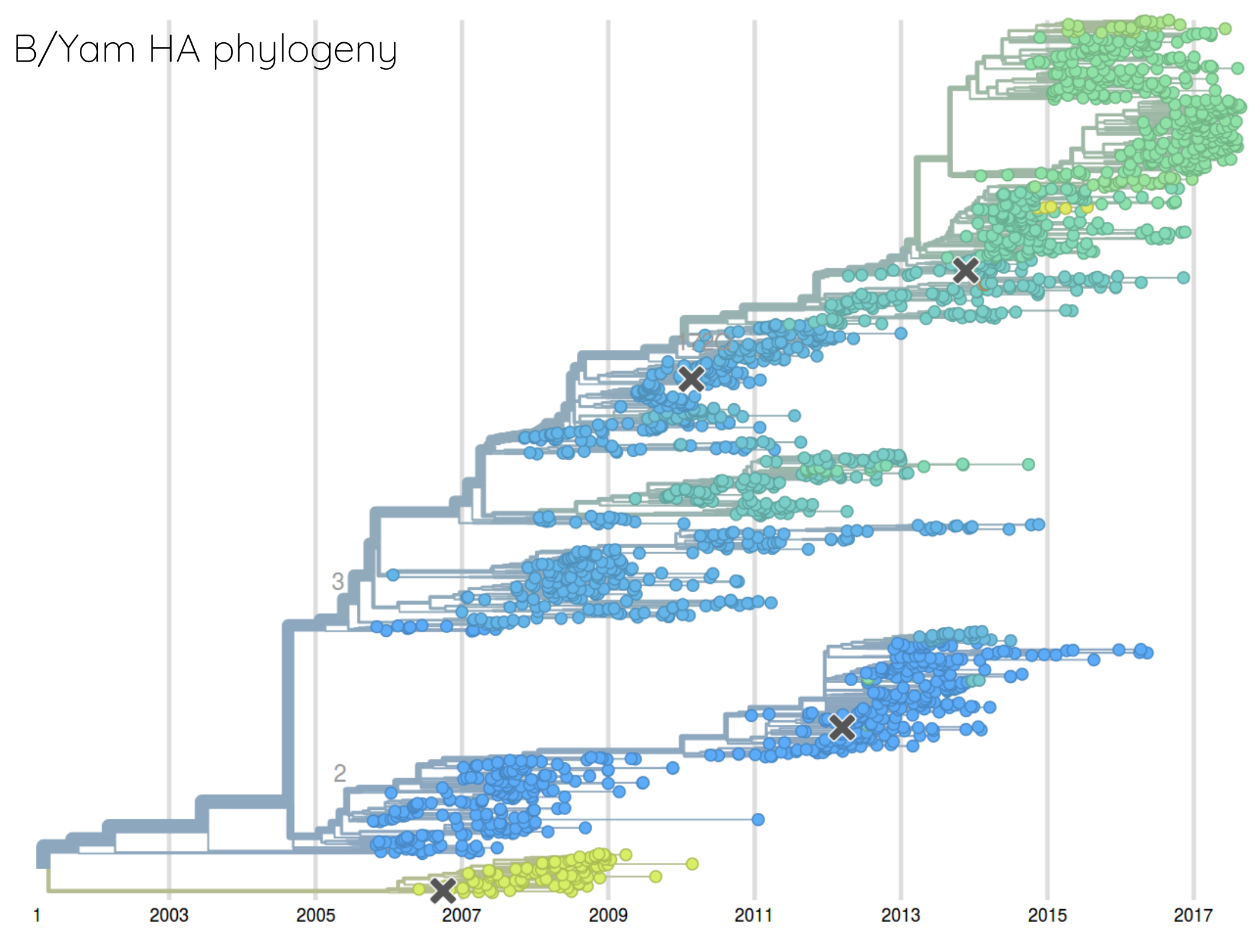
Influenza B viruses have split into two lineages
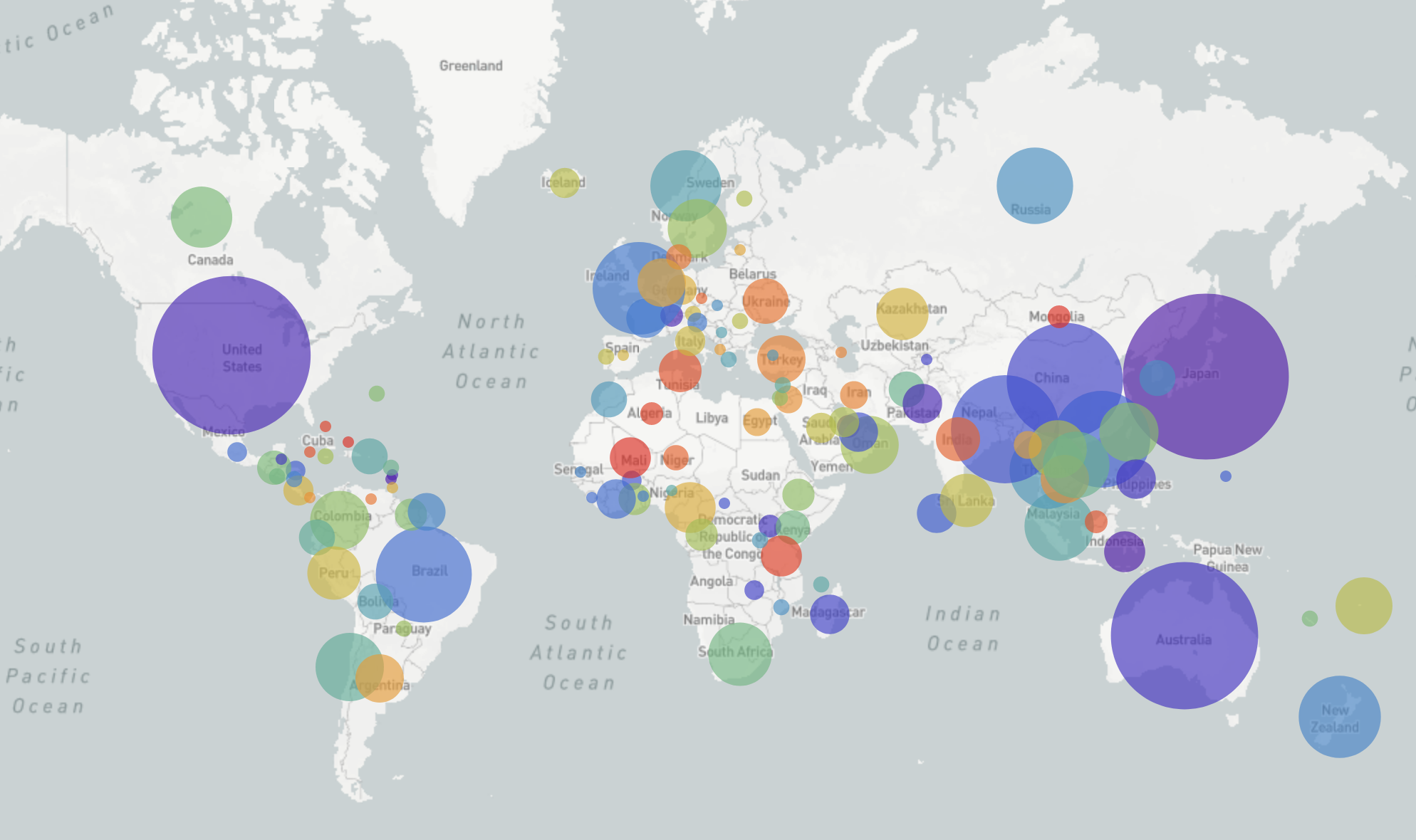
GISRS and GISAID -- Influenza virus surveillance
- comprehensive coverage of the world
- timely sharing of data through GISAID -- often within 2-3 weeks of sampling
- hundreds of sequences per week (in peak months)
→ requires continuous analysis and easy dissemination
→ interpretable and intuitive visualization
nextflu.org
joint project with Trevor Bedford & his lab
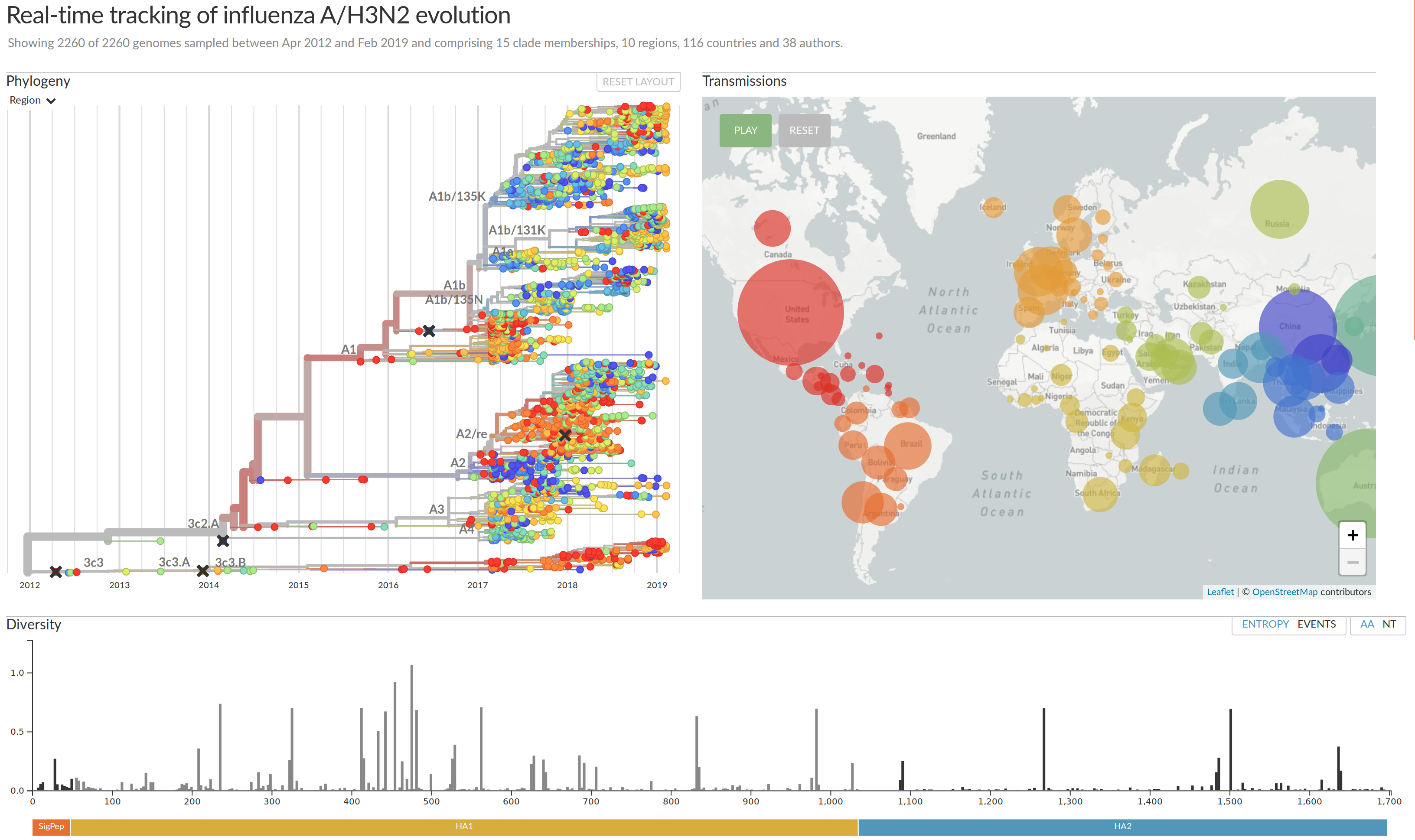
Beyond tracking: can we predict?
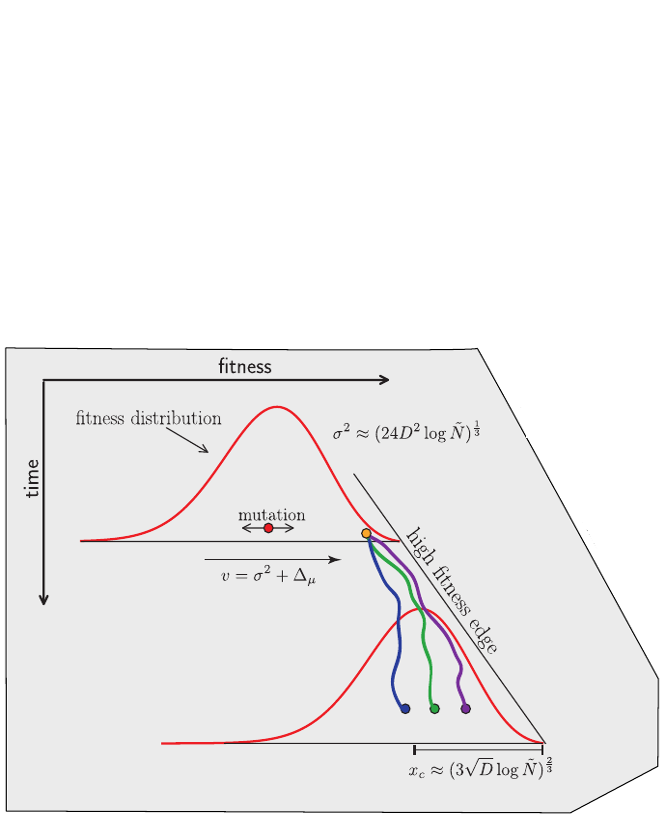
Fitness variation in rapidly adapting populations
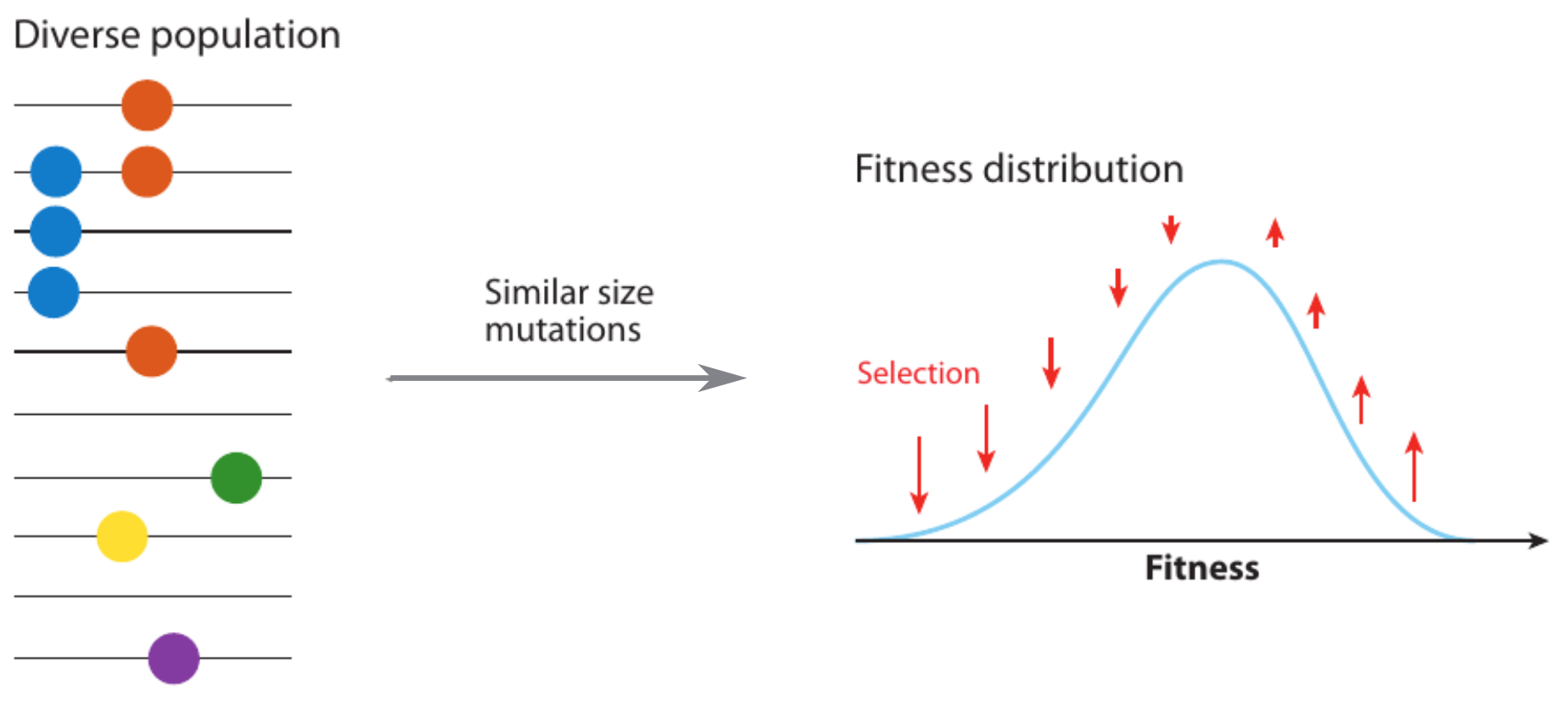
- Speed of adaptation is logarithmic in population size
- Environment (fitness landscape), not mutation supply, determines adaptation
- Different models have universal emerging properties
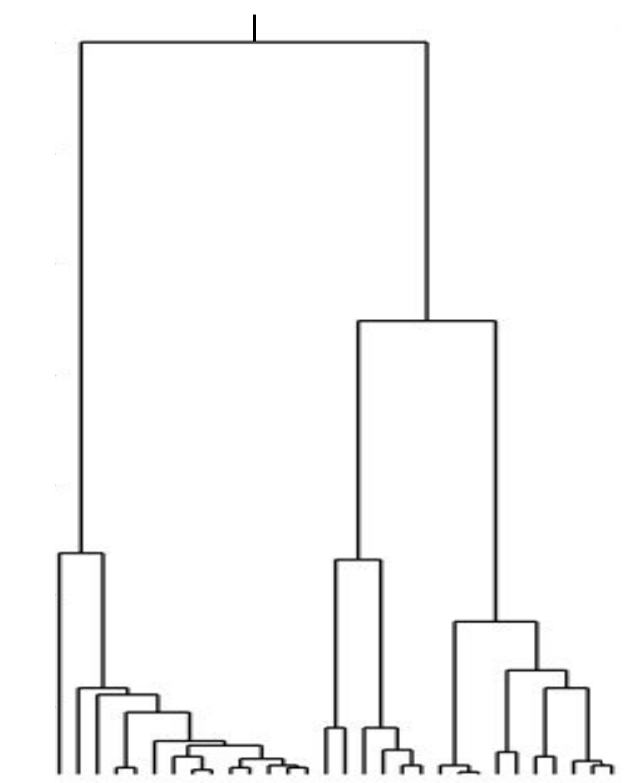
Neutral/Kingman coalescent
strong selection
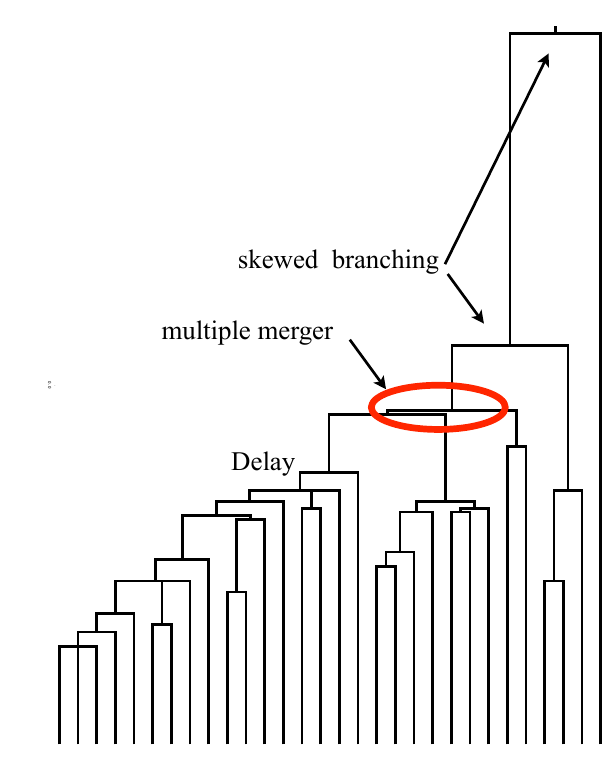
Bolthausen-Sznitman Coalescent
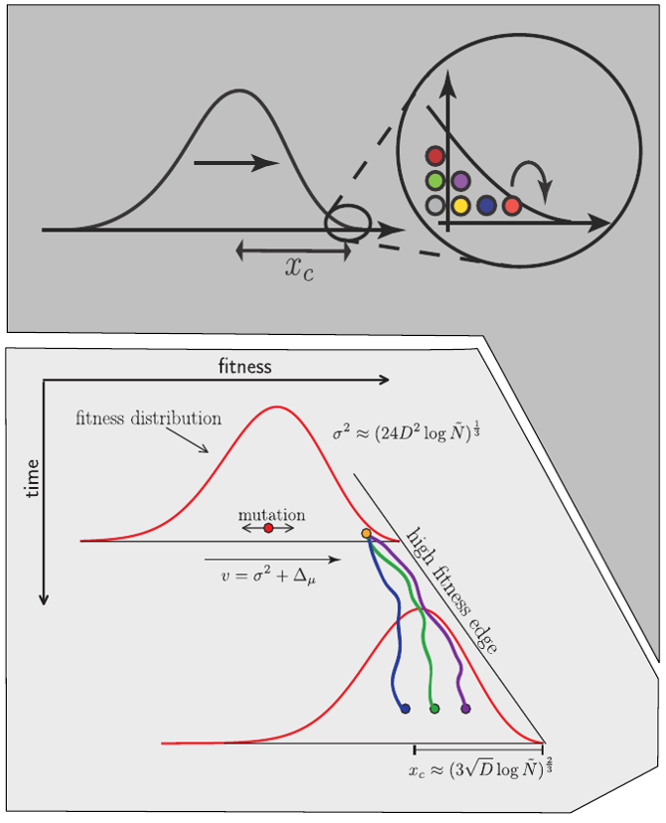
Burst in the tree ↔ high fitness
Predicting evolution
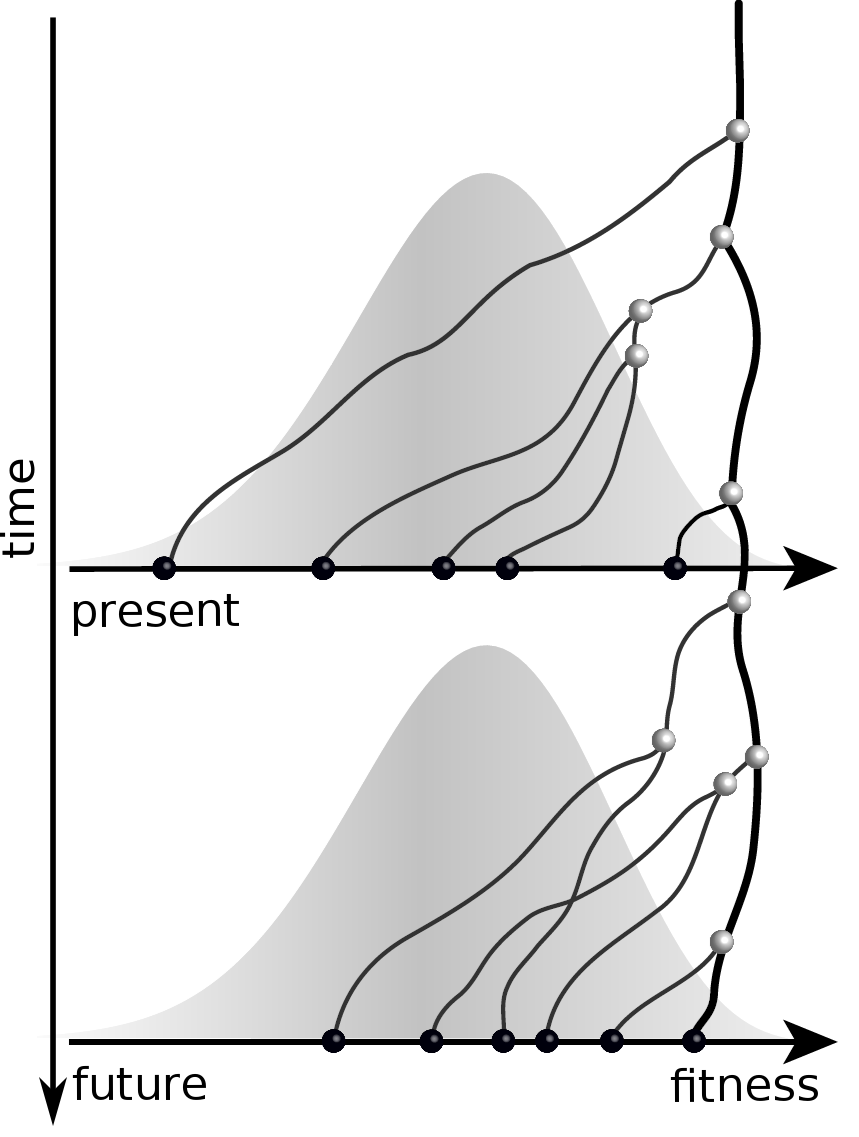
Given the branching pattern:
- can we predict fitness?
- pick the closest relative of the future?
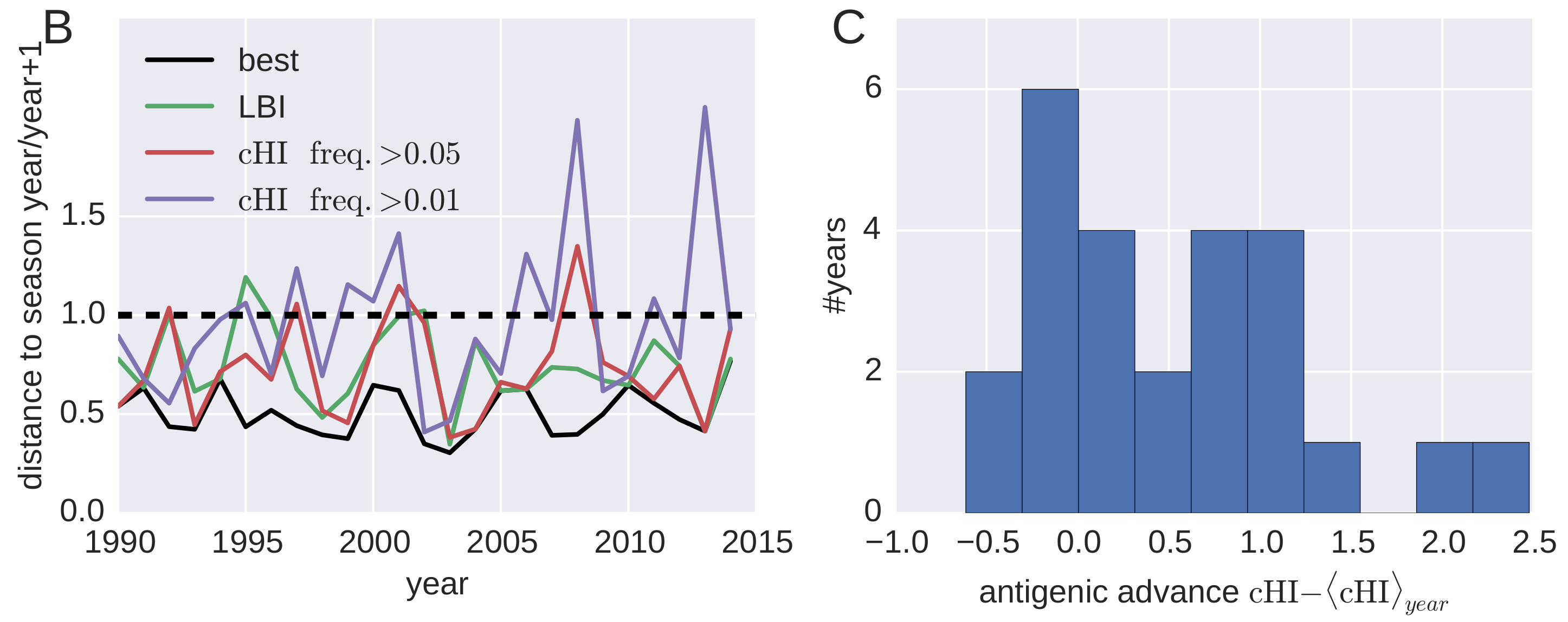
Prediction of the dominating H3N2 influenza strain
- no influenza specific input
- how can the model be improved? (see model by Luksza & Laessig)
- what other context might this apply?
Hemagglutination Inhibition assays
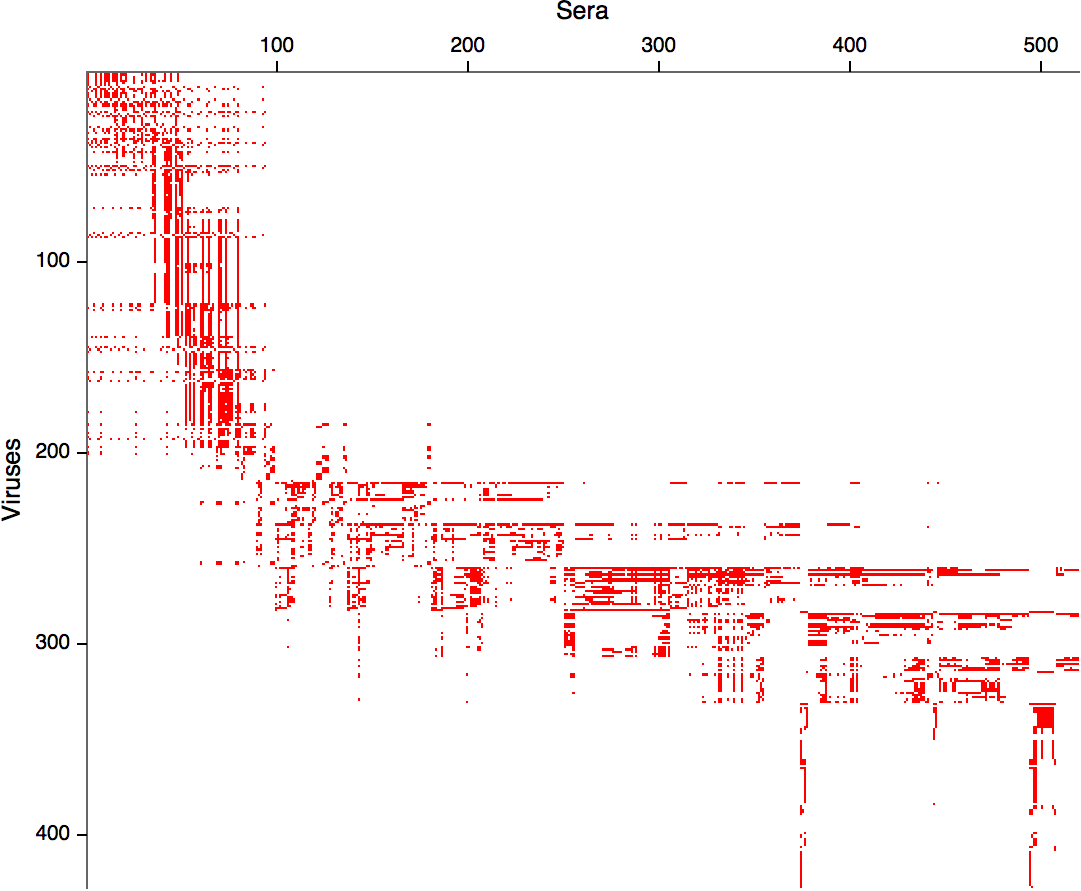
HI data sets
- Long list of distances between sera and viruses
- Tables are sparse, only close by pairs
- Structure of space is not immediately clear
- MDS in 2 or 3 dimensions
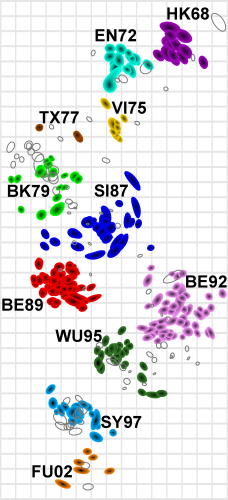Smith et al, Science 2002
Integrating antigenic and molecular evolution
- $H_{a\beta} = v_a + p_\beta + \sum_{i\in (a,b)} d_i$
- each branch contributes $d_i$ to antigenic distance
- sparse solution for $d_i$ through $l_1$ regularization
- related model where $d_i$ are associated with substitutions
Integrating antigenic and molecular evolution
- MDS: $(d+1)$ parameters per virus
- Tree model: $2$ parameters per virus
- Sparse solution
→ identify branches or substitutions that cause titer drop
Rate of antigenic evolution
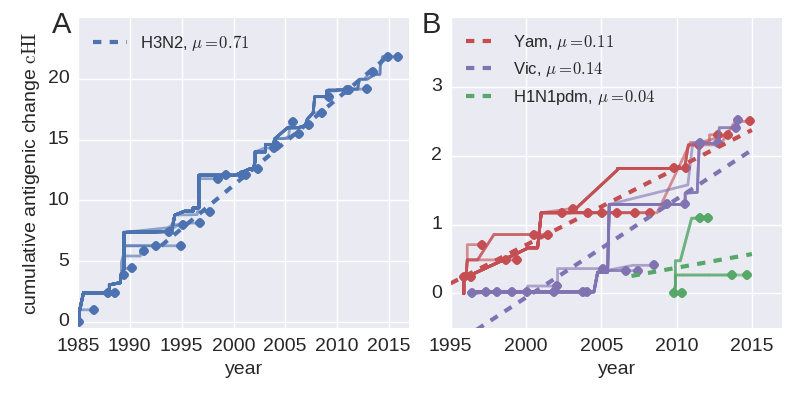
- Cumulative antigenic evolution since the root: $\sum_i d_i$
- A/H3N2 evolves faster antigenically
- A/H3N2 has a more rapid population turn-over
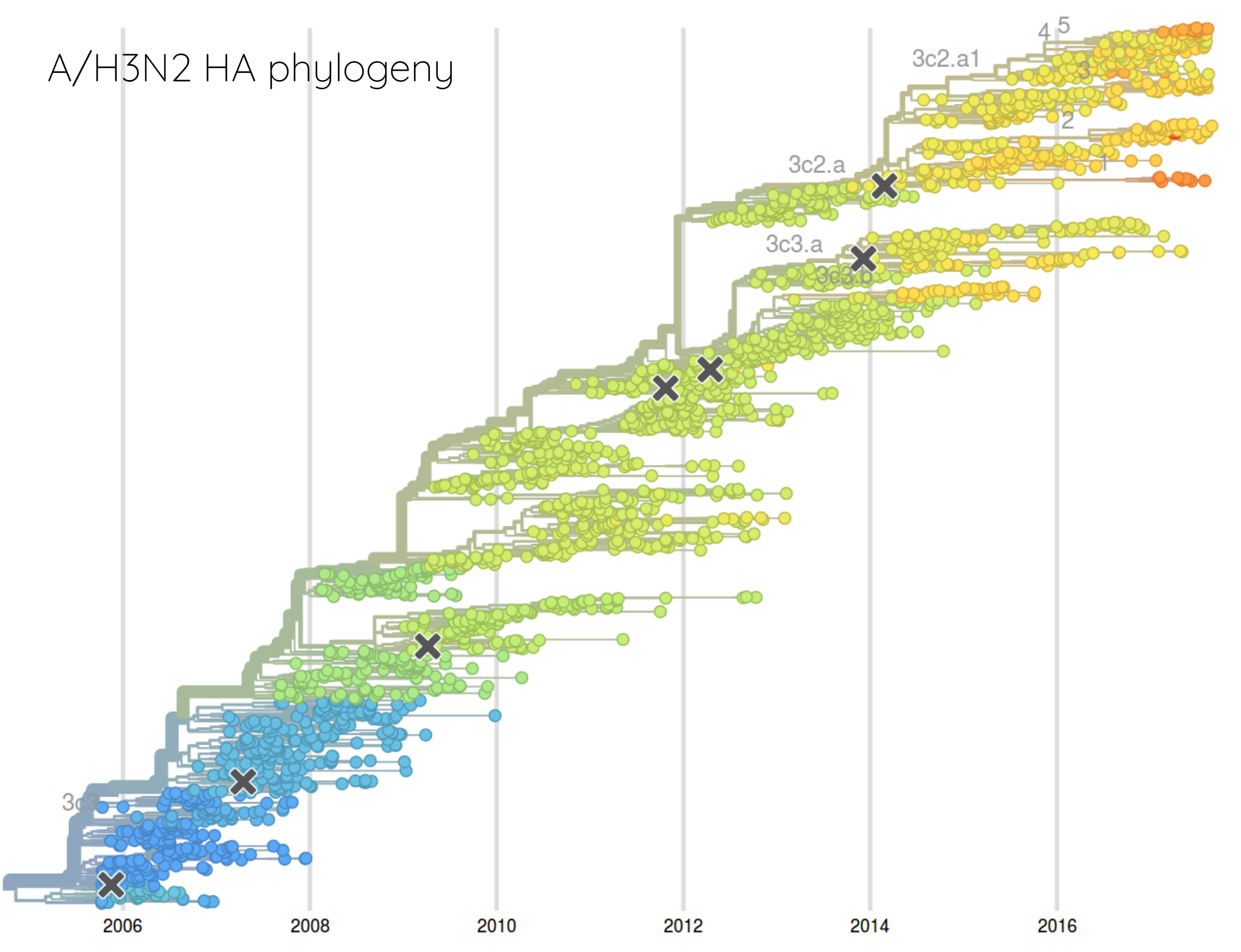
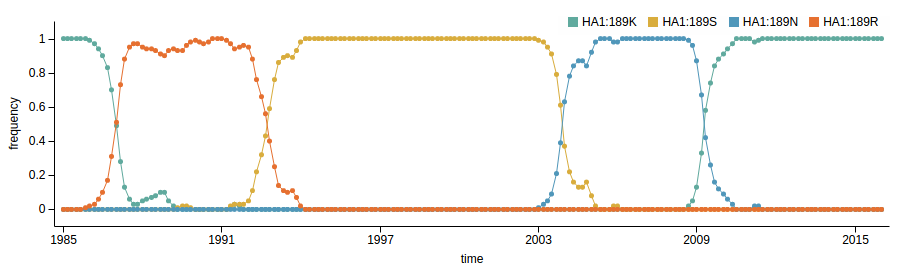
How many sites are involved?
| Mutation | effect |
| K158N/N189K | 3.64 |
| K158R | 2.31 |
| K189N | 2.18 |
| S157L | 1.29 |
| V186G | 1.25 |
| S193F | 1.2 |
| K140I | 1.1 |
| F159Y | 1.08 |
| K144D | 1.08 |
| K145N | 0.91 |
| S159Y | 0.89 |
| I25V | 0.88 |
| Q1L | 0.85 |
| K145S | 0.85 |
| K144N | 0.85 |
| N145S | 0.85 |
| N8D | 0.73 |
| T212S | 0.69 |
| N188D | 0.65 |
Predicting successful influenza clades
Acknowledgments
- Trevor Bedford
- Pavel Sagulenko
- James Hadfield
- Emma Hodcroft
- Tom Sibley
- and others
Influenza and Theory acknowledgments
- Boris Shraiman
- Colin Russell
- Trevor Bedford
- Oskar Hallatschek
- All the NICs and WHO CCs that provide influenza sequence data
- The WHO CCs in London and Atlanta for providing titer data
- The GISAID initiative for influenza sequence data sharing
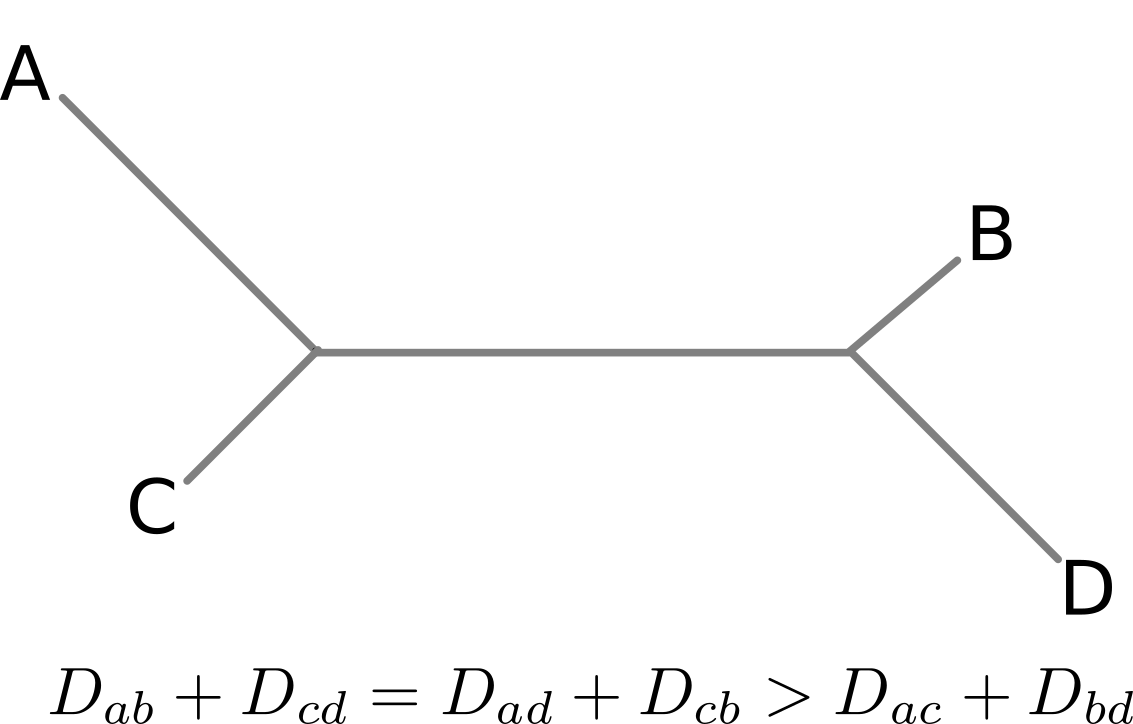
Are antigenic distances tree-like?
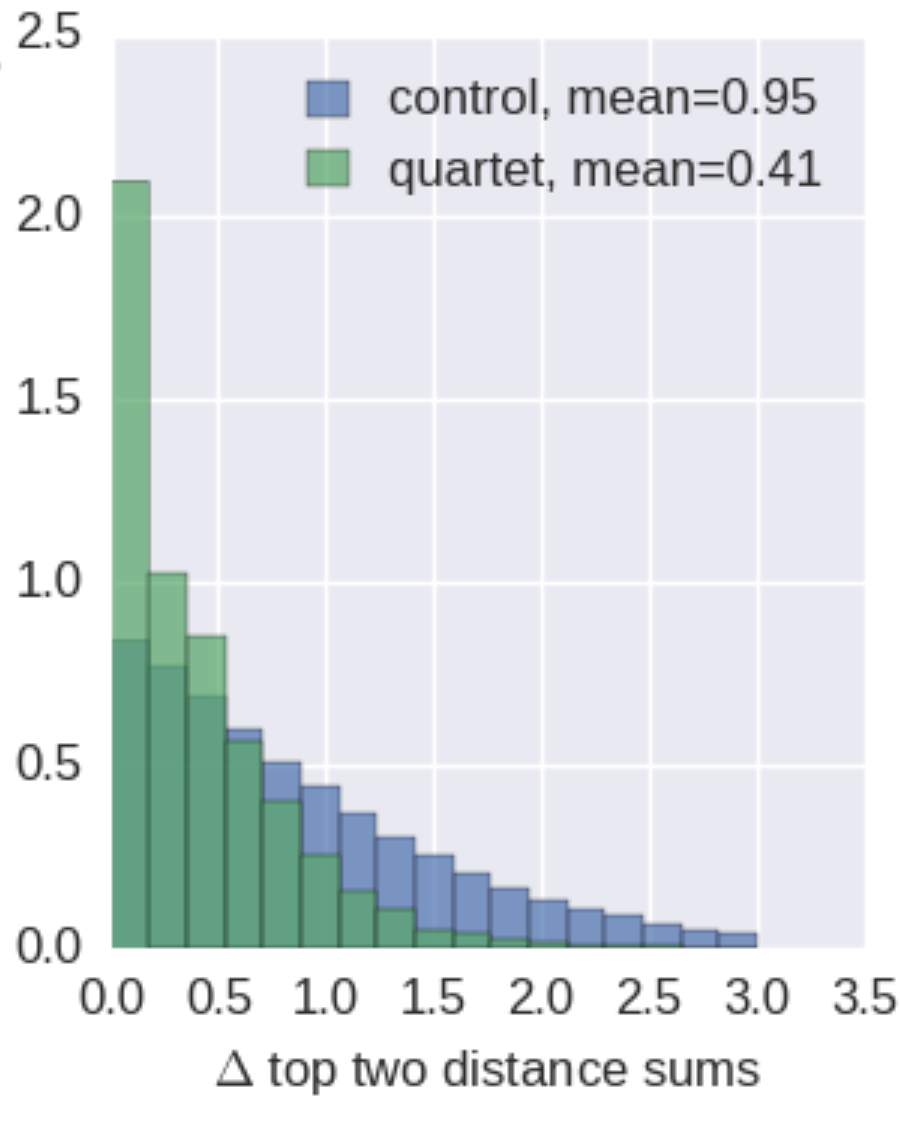
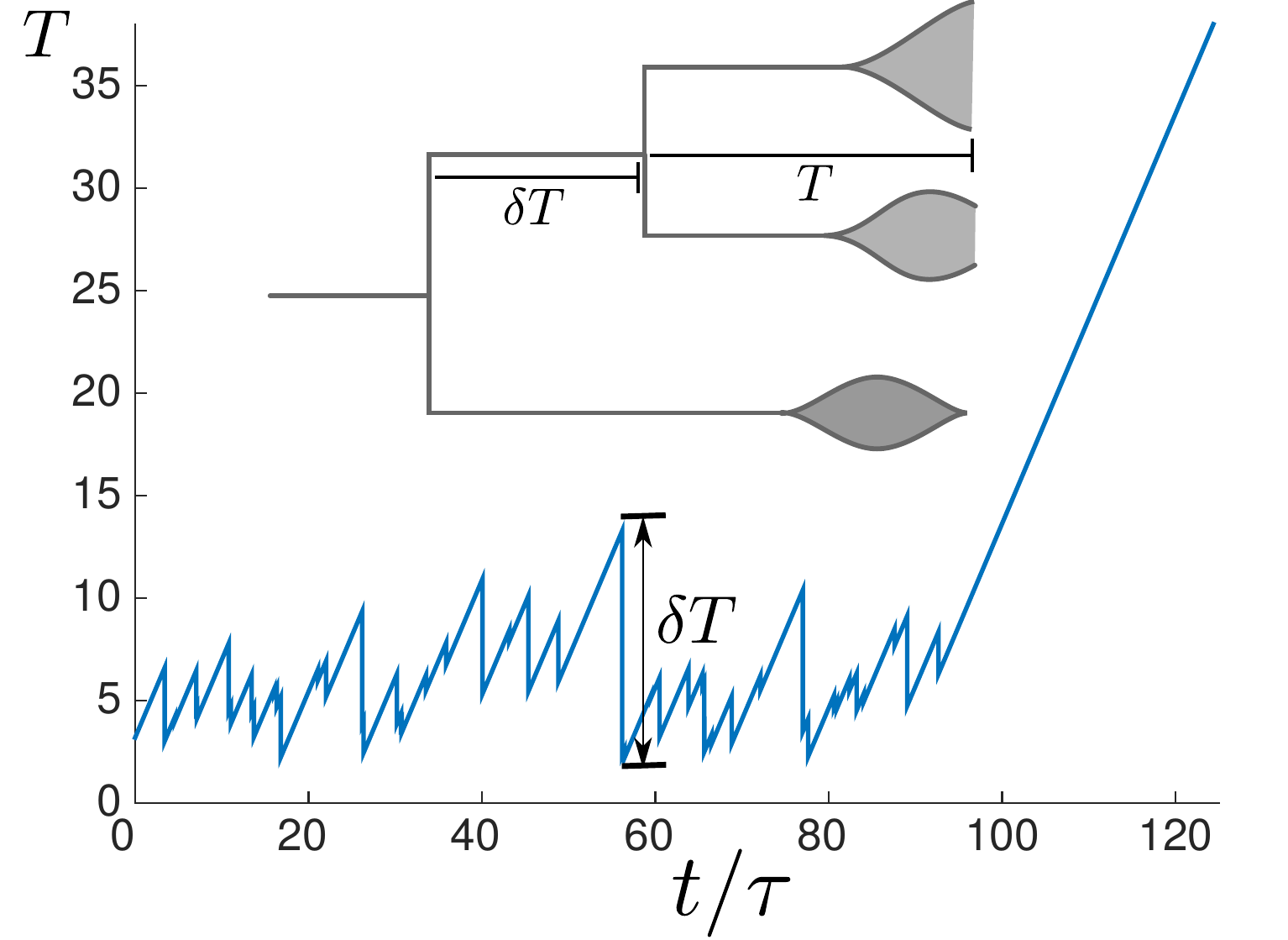
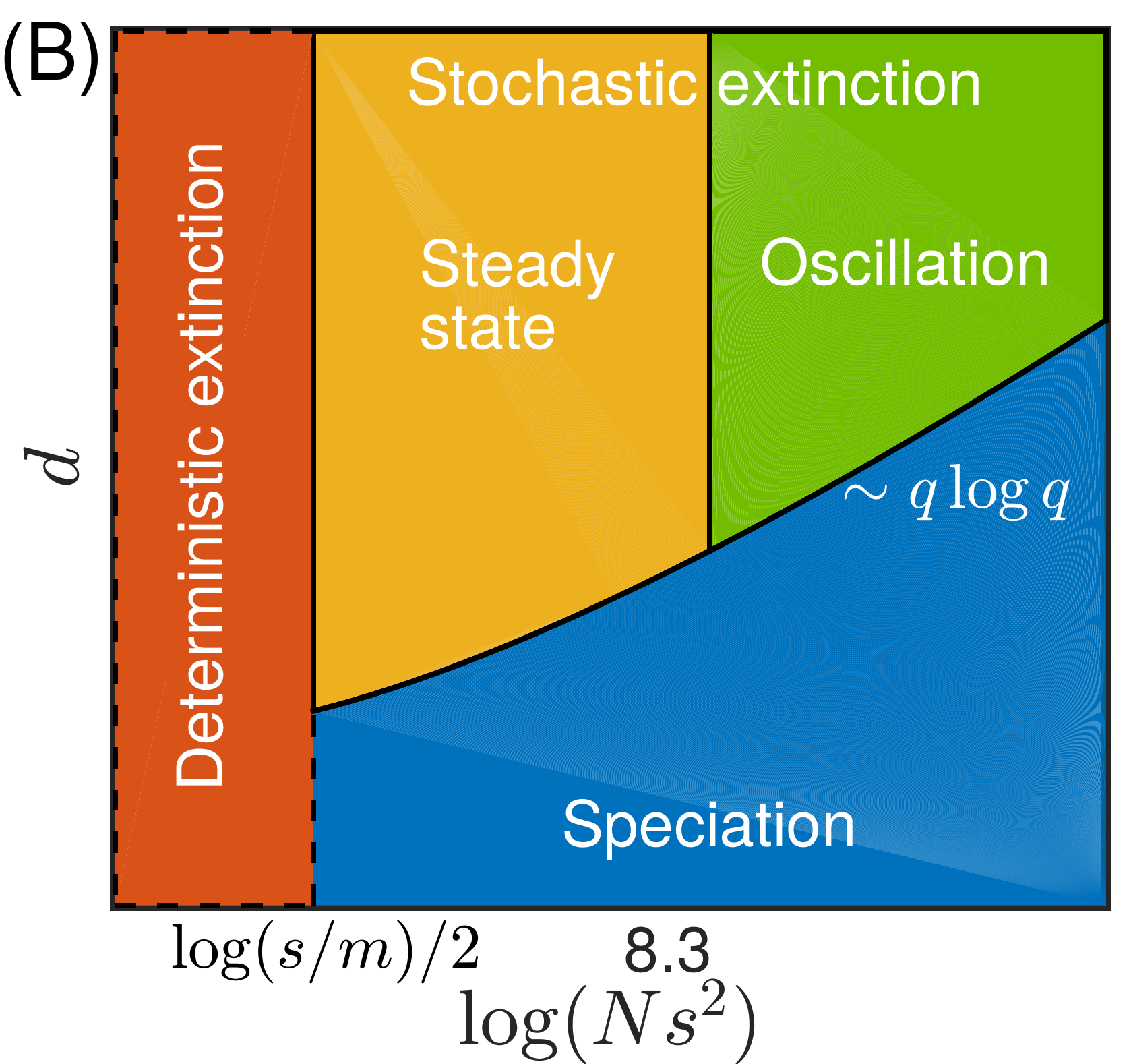
There are many ways to escape immunity -- why doesn't influenza speciate?
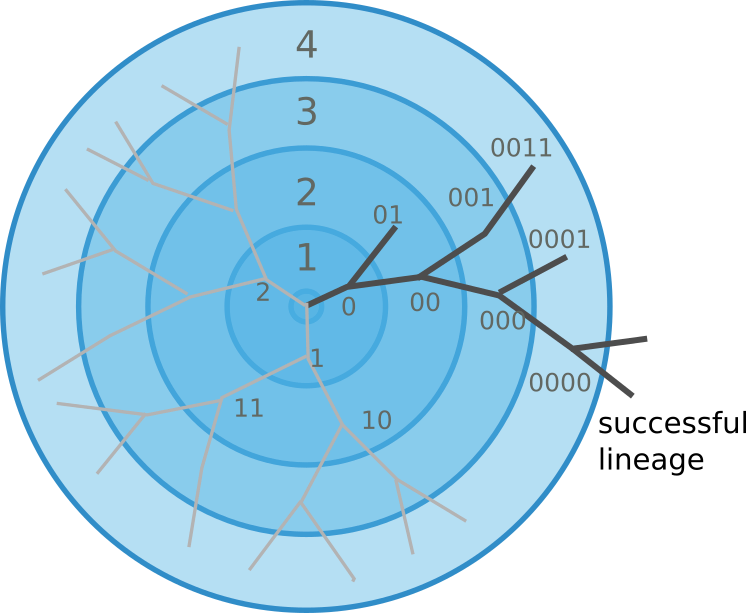
There are many ways to escape immunity -- why doesn't influenza speciate?
Combining SIR-models and rapid molecular adaptation
- Infections with strain $a$: $\frac{d I_a}{dt} = \beta S_a I_a - (\nu+\gamma)I_a$
- Susceptibility to strain $a$: $S_a =e^{-\sum_b K_{ab} R_b }$
- Recovered from stain $a$: $\frac{d R_a}{dt} = \nu I_a - \gamma R_a$
- Cross-immunity: $K_{ab} = e^{-\frac{|a-b|}{d}}$
- Mutations from $a\to b$ reduce cross-immunity and increase susceptibility
- Antigenic evolution is essential to establish seasonal patterns
Transition from pandemic to seasonal patterns
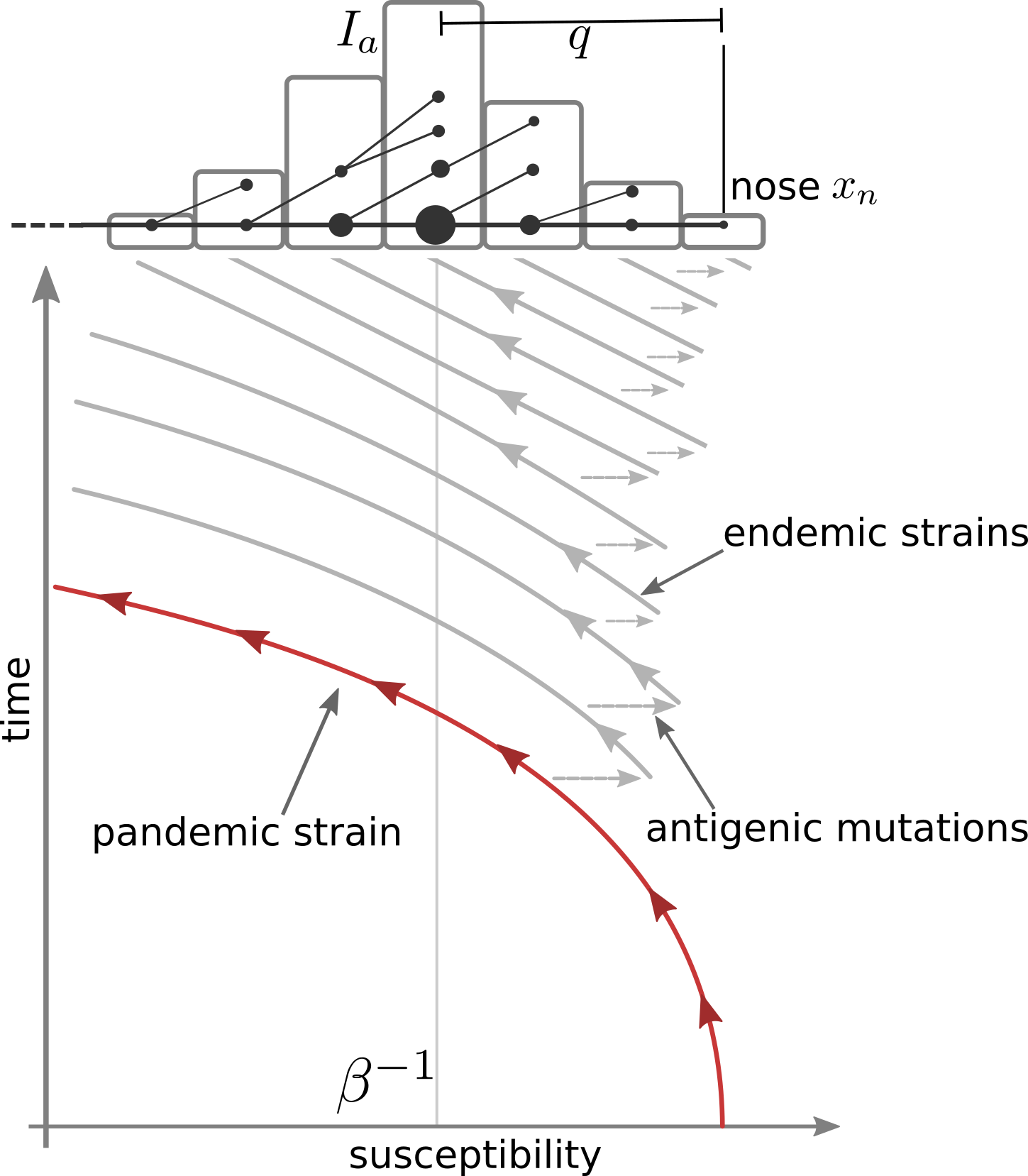
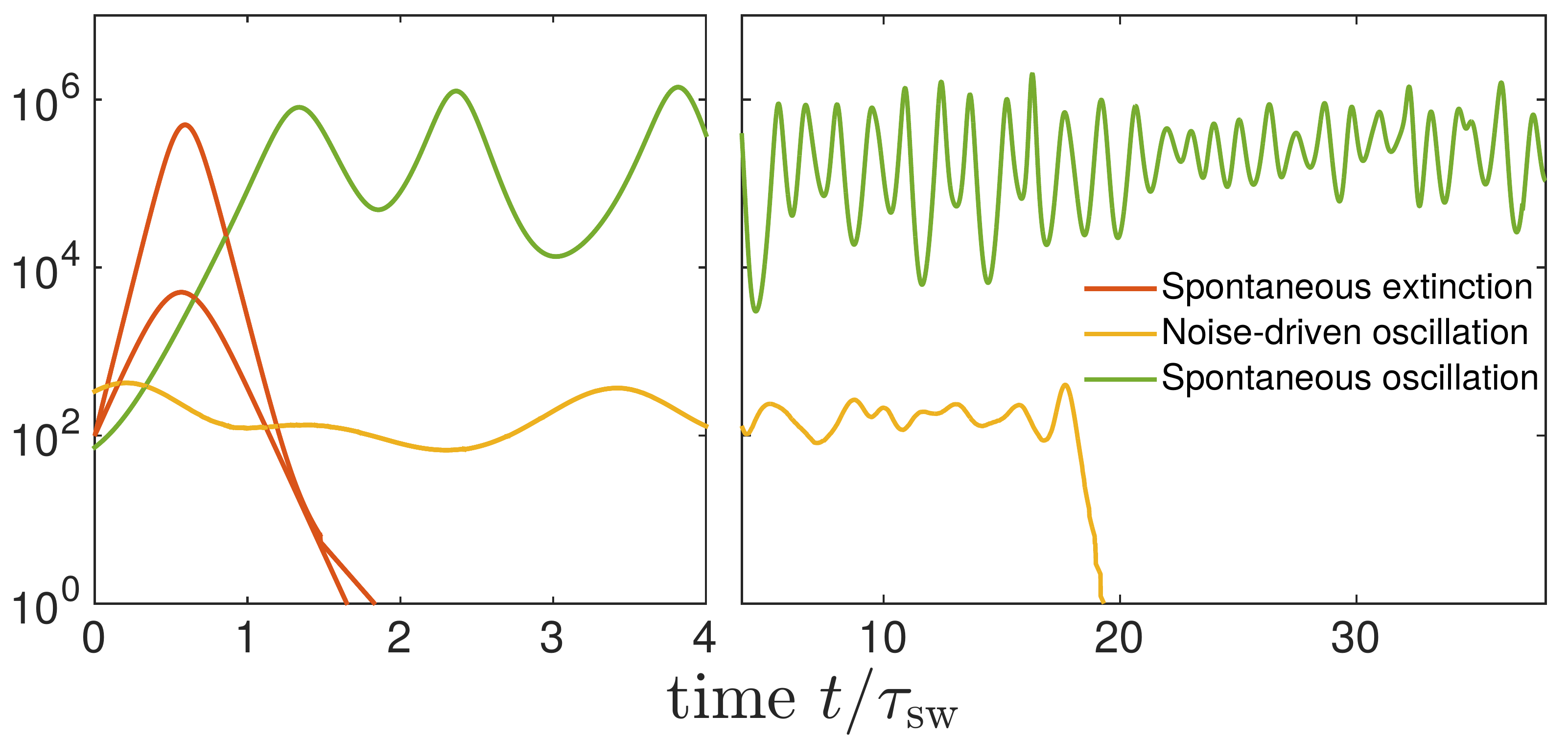
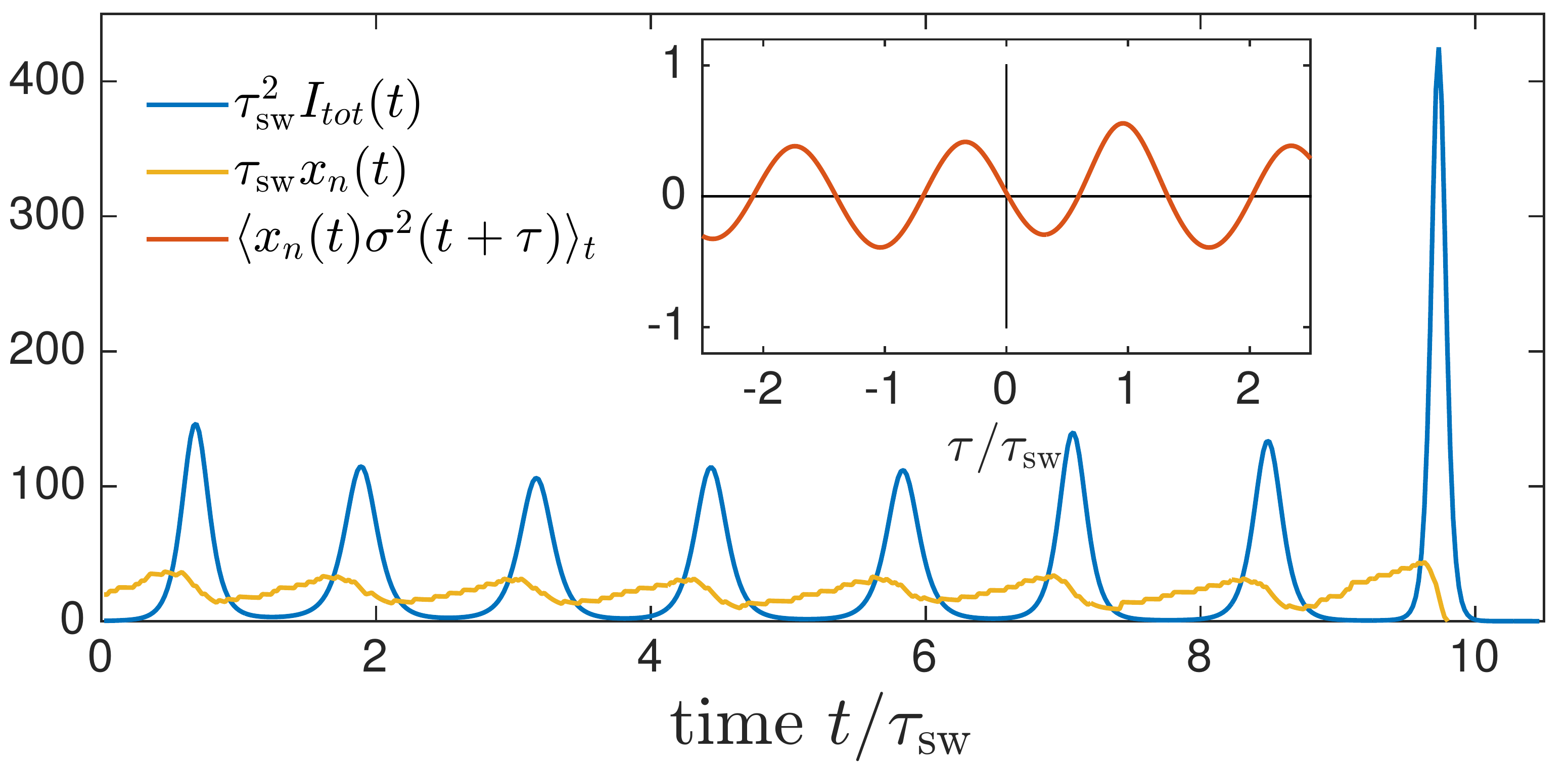
Speciation into antigenically distinct lineages
