PoL I: Quantitative problems, dimensions, and units
Richard Neher
Biozentrum, University of Basel
Can we understand biology quantitatively?
How is Biology different from Physics?
How can Physics help understand biological systems?
Mathematics is extremely effective in physics
- Motions of planets and moons can be predicted with extreme accuracy
- Behavior of atoms, particles, electrons etc can be controlled and exploited
- Unintuitive behavior is captured by physical theories
Biology is much more complex than Physics
Physics is most effective in simple and controlled systems
Biological complexity
- Laws of physics connect fundamental particles and forces.
- Physics often describe homogenous or simple matter.
Biological complexity
- Biological systems evolved -- layering complexity
- Cells consist of thousands of molecular species, interacting in complicated ways
- Biology is always in flux.
Much of biology describes complex dependencies in qualitative terms:
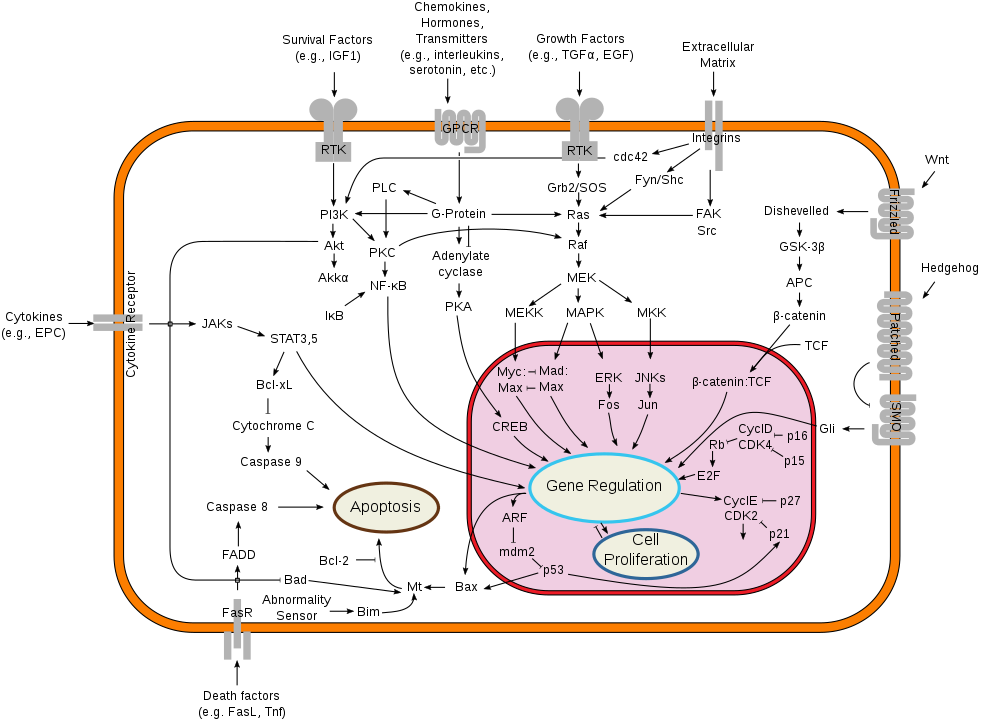Wikipedia, by cybertory
Is there hope? YES!
Quantitative questions
- How rapidly does a protein move from one end of the cell to another?
- How many ribosomes/signaling molecules are in a cell?
- What fraction of transcription factors is bound to DNA?
- What are the speed limits for biochemical reactions?
- How are polarities and developmental gradients set up?
- How many human cells are in your body?
- How many other cells?
- Not: Gene X causes Y
- But: 20% faster diffusion of gene X extends the gradient by $20\mu m$
Dimensions and units
Dimensions
- length
- weight
- energy
- current
- force
- temperature
- ....
Units:
- length: meters, miles, feet, Angstrom
- weight: grams, stones,
- energy: Joules, calories
- current: ampere
- force: Newton
- temperature: Celsius, Kelvin
- ....
- Dimensions describe the nature of a quantity
- Units are conventions to measure them
Comparing quantities
- Only quantities of the same dimension can be compared: length $X$ is greater than length $Y$ etc. There is no sense is which length $X$ can be greater than weight $Y$.
- Units are conventions -- there is nothing fundamental about them.
- Some unit systems are more convenient than others.
- Everyday units are often inconvienent for biological processes
- We can pick units to make things as simple as possible
Laws of physics relate quantities of different dimensions
Take Newton's law:
$$ F = m \times a$$ $$ \mathrm{Force} = \mathrm{mass} \times \mathrm{acceleration}$$
Relates quantities of different dimensions to each other.
$$ F = m \times a$$ $$ \mathrm{Force} = \mathrm{mass} \times \mathrm{acceleration}$$
Relates quantities of different dimensions to each other.
Common units for the quantities involved are:
$$ \mathrm{[Newton]} = \mathrm{[Kilogram]} \times \mathrm{[meter/second^2]}$$
thereby defining the unit of force "Newton".
$$ \mathrm{[Newton]} = \mathrm{[Kilogram]} \times \mathrm{[meter/second^2]}$$
thereby defining the unit of force "Newton".
The law is valid in any system of units!
Units are chosen by humans, the law itself is fundamental.
Units are chosen by humans, the law itself is fundamental.
Physical constants
Consider the gravitational law:
$$ F \sim \frac{m_1 m_2}{r^2}$$ $$ \mathrm{Force} \sim \mathrm{mass^2}/\mathrm{length^2}$$
The quantities left and right do not have the same dimensions!
Links force to masses and distance, but not what the absolute value of the force is.
$$ F \sim \frac{m_1 m_2}{r^2}$$ $$ \mathrm{Force} \sim \mathrm{mass^2}/\mathrm{length^2}$$
The quantities left and right do not have the same dimensions!
Links force to masses and distance, but not what the absolute value of the force is.
The missing link is established by the gravitational constant $G$:
$$ F = G\frac{m_1 m_2}{r^2}\quad \mathrm{with} \quad G \approx 6.67 \frac{m^3}{kg\,s^2}$$
The value of $G$ depends on the system of units we use.
$$ F = G\frac{m_1 m_2}{r^2}\quad \mathrm{with} \quad G \approx 6.67 \frac{m^3}{kg\,s^2}$$
The value of $G$ depends on the system of units we use.
This course: quantitative understanding of biology
- Laws of physics yield quantitative and predictive relationships and constraints for biology
- Computer programming is essential to explore quantitative relationships and handle data
- Units are absolutely critical to get right:
If you calculate a length and the result is in seconds something went seriously wrong - Checking your units will catch many obvious mistakes.
- Choosing your units wisely will make many calculations easier