Problem 1
Verify that \(P(x,n)\) solves the Master equation
$$P(x,n+1) = pP(x-1,n) + (1-p)P(x+1,n)$$
We established in the lecture, that \(x=2k-n\) where \(l\) is binomially distributed. Now observe that \(P(x,n+1)\) is binomial with \(k=(x+n+1)/2\), \(P(x-1,n)\) is binomial with \(k' = (x-1+n)/2 = k-1\), and \(P(x+1,n)\) is binomial with \(k''=(x+1+n)/2=k\). Hence we need to show that binomial distributions observe
$$P(k,n+1) = pP(k-1,n) + (1-p)P(k,n) = p^k (1-p)^{n+1-k} n!\left[\frac{1}{(k-1)!(n-k+1)!} + \frac{1}{(k-n)!(n-k)!}\right] $$
Rearranging left right hand side, we have
$$P(k,n+1) = p^k (1-p)^{n+1-k} n!\left[\frac{k}{k!(n-k+1)!} + \frac{n-k+1}{(k-n)!(n-k+1)!}\right] = \frac{(n+1)!}{k!(n-k+1)!}p^k(1-p)^{n-k+1}$$
and we are done!
Problem 2
Show that
$$P(x,t) = \frac{1}{\sqrt{4\pi Dt}}e^{-\frac{(x-vt)^2}{4Dt}}$$
solves the diffusion equation. Of course this would be easier if \(v=0\). If, however, we look at the solution in terms of the variable \(y=x-vt\), there is no sign of \(v\) in the solution:
$$P'(y,t) = \frac{1}{\sqrt{4\pi Dt}}e^{-\frac{y^2}{4Dt}}$$
In other words, in a coordinate system that moves with velocity \(v\), our problems behaves has if velocity was zero. But we need to tranform the diffusion equation to the new system of variables. At constant \(y\), the derivative of \(P'\) with respect to \(t\) picks up the translation term:
$$\frac{\partial P'(t,y)}{\partial t} = \frac{d P(t,y+vt)}{d t} = \frac{\partial P(t,y+vt)}{\partial t} + v \frac{\partial P(t,y+vt)}{\partial x}$$
When keeping \(t\) constant, nothing changes and \(dx = dy\). Hence in terms of \(P'(y,t)\), the diffusion equation looks like this:
$$\frac{\partial P(t,x)}{\partial t} = \frac{\partial P'(t,y)}{\partial t} - v \frac{\partial P'(t,y)}{\partial y} = \frac{\partial^2 P'(t,y)}{\partial y^2} - v \frac{\partial P'(t,y)}{\partial y}$$
And we find that in the variable \(y=x-vt\), there is no advection term. Without the advection term, solving the diffusion equation is not too hard.
$$\frac{\partial P(x,t)}{\partial t} = \frac{e^{-x^2/4Dt}}{\sqrt{4\pi Dt}} \left[-\frac{1}{2t} + \frac{x^2}{4Dt^2}\right] $$
For the two derivatives with respect to \(x\), we get
$$ \frac{\partial P(x,t)}{\partial x^2} = \frac{e^{-x^2/4Dt}}{\sqrt{4\pi Dt}} \left[\frac{x^2}{4 Dt^2} - \frac{1}{2t}\right] $$
which are obviously equal.
Problem 3
The solution to the diffusion equation with absorbing boundary at \(x=0\) with an spike at \(x=x_0\) at time \(t=0\) is
$$P(x,t) = \frac{1}{\sqrt{4\pi Dt}}\left[e^{-(x-x_0)^2/4Dt} - e^{-(x-x_0)^2/4Dt}] $$
The flux is \(j(x,t) = -D\frac{\partial}{\partial x}P(x,t)\) and evaluates to
$$j(x,t) = \frac{D}{\sqrt{4\pi Dt}} \left[\frac{x-x_0}{2Dt}e^{-(x-x_0)^2/4Dt} - \frac{x+x_0}{2Dt}e^{-(x+x_0)^2/4Dt}\right]$$
At \(x=0\), this simplified to
$$j(0,t) = -\frac{e^{-x_0^2/4Dt}}{\sqrt{4\pi D}} \frac{x_0}{t^{3/2}} $$
Note that this solution is governed by the time scale \(\tau = x_0^2/4D\) which determines how rapidly the particles are absorbed. To get an idea of the time dependence of this flux, lets plot it
import matplotlib.pyplot as plt
import numpy as np
def flux(t,x0, D):
return np.exp(-x_0**2/(4*D*t))/np.sqrt(4*np.pi*D)*x_0/t**1.5
t = np.linspace(0,3,1001)
D = 1
x_0 = 1
plt.figure()
plt.plot(t, flux(t,x_0,D))
plt.savefig('diffusion_flux.png')
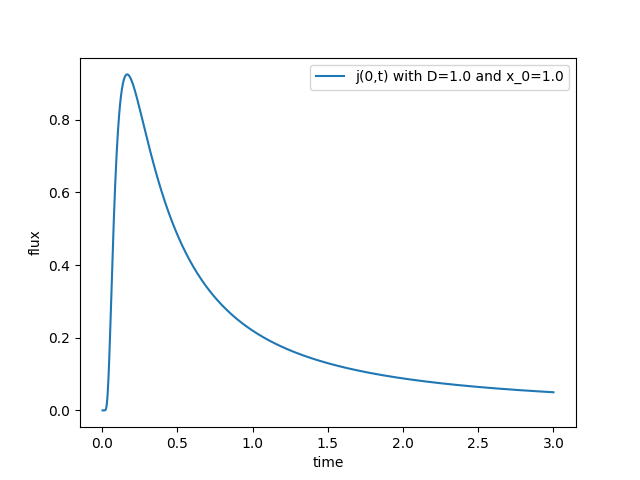
Does all of the solution gets eventually absorbed? (it does, the original solution tends to zero with \(t\to\infty\)) Hence the integral of the flux over time should equal one!
$$1 = \int_0^\infty dt \frac{e^{-x_0^2/4Dt}}{\sqrt{4\pi D}} \frac{x_0}{t^{3/2}} $$
To evaluate this, substitute \(y = x_0/\sqrt{2Dt}\). The derivative \(dy/dt = -x_0/\sqrt{8D} t^{-3/2} \).
$$\sqrt{\frac{2}{\pi}} \int_0^\infty \frac{dt}{\sqrt{8D}t^{3/2}} e^{-x_0^2/4Dt} = \sqrt{\frac{2}{\pi}} \int_0^\infty dy e^{-y^2/2} = 1$$
So yes, we explicitly confirm that the flux integrates to one and in one dimension we inevitably hit the absorbing boundary, no matter how far away we start.