Small object are constantly bounced around by thermal motions of surrounding molecules. This dynamics is called Brownian motion in honour of the botanist Robert Brown who noticed jittering of pollen grains under a microscope.
By Lookang Author of computer model: Francisco Esquembre, Fu-Kwun and lookang - Own work, CC BY-SA 3.0, Link
Despite (because) of the randomness of the process, the laws governing Brownian motion are simple and universal.
Discrete random walks
Consider a object at position \(x\) that at every time step moves 1 unit to the right with probability \(p\) and to the left with probability \(1-p\). Its displacement after \(n\) steps will be \(\Delta x = 2k-n\) where \(k\) is number of steps to the right. The distribution of displacements evidently follows a binomial distribution with
$$P(k,n) = \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}$$
The average displacement is simply given by
$$\langle \Delta x \rangle = 2\langle k \rangle - n = 2np \sum_k \frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{n-k} - n = (2p-1)n$$
For a symmetric random walk with \(p=0.5\), the average displacement is zero as expected for random walks. This expression characterizes the average behavior, but the essence of Brownian motion lies in their randomness. To quantify the randomness in displacement, one typically looks at the mean squared deviation, the is the variance of the process.
$$\langle (\Delta x - \langle \Delta x\rangle)^2\rangle = \langle (2k-n - (2p-1)n)^2\rangle = 4\langle (k - p n)^2\rangle = 4\langle k^2 - p^2 n^2\rangle=4\langle k(k-1) + np - p^2 n^2\rangle$$
We have hence reduced the problem of calculating the variance to calculating the second moment. The very last step was merely a convenience transformation:
$$\langle k(k-1)\rangle= p^2 n(n-1)\sum_k \frac{(n-2)!}{(k-2)!(n-k)!}p^{k-2}(1-p)^{n-k} = p^2 n(n-1) $$
Plugging this back into the above, we get
$$\langle (\Delta x - \langle \Delta x\rangle)^2\rangle = (4\langle k(k-1) + np - p^2 n^2 = 4n(p-p^2) = 4np(1-p) $$.
The important observation is that the variance grows linearly with time, that is the number of steps \(n\). Since the variance is "distance squared", the typical displacement only grows with the square root of time. This is a universal property of diffusive processes: Due to the cancellation of random backwards and forward jitter, displacements don't grow linearly in time as they would in ballistic (directed) motion.
Master equations
Above, we have written down the probability distribution of the position of our random walker right away because we knew the answer from elementary combinatorics. We won't always be so lucky. So lets explore a more general way of looking at the problem. Consider the probability \(P(x,n)\) of observing our particle at position \(x\) at time \(n\). We can write down the following equation for the distribution at time \(n+1\):
$$P(x,n+1) = pP(x-1,n) + (1-p)P(x+1,n) $$
where the first term corresponds to hops towards the right, the second term to the left.
Very that the distribution from above \(P(x,n)\) solves this equation!
Diffusion in continuous time and space
Above we assumed that our particle is moved by a fixed amount at each time interval. That is of course not what actually happens. In reality, every object is bombarded by many molecules every nano-second and follows a continuous trajectory. Let make time continuous first and assume discrete left/right jumps happen with rate \(\nu\). \(P(x,t+\Delta t)\) the obeys
$$P(x,t+\Delta t) = (1-\nu\Delta t)P(x,t) + \frac{\nu\Delta t}{2} (P(x-1,t) + P(x+1,t)) $$
which can be rearranged into a differential equation
$$\frac{d P(x,t)}{dt} = \frac{\nu}{2} (P(x-1,t) - 2P(x,t) + P(x+1,t))$$
The combination of terms on the right is a discrete approximation of a second derivative that we'll come across again below.
Let's do away with the discrete steps and just assume that there is a certain function \(g(\delta x, \delta t)\) that describes the distribution of displacement \(\delta x\) after an infinitesimal time \(\delta t\). We can write
$$P(x,t+\Delta t) = \int d\delta x g(\delta x, \Delta t) P(x-\delta x, t) \approx \int d\delta x g(\delta x, \Delta t) \left[ P(x, t) - \delta x \frac{\partial P(x,t)}{\partial x} + \frac{\delta x^2}{2} \frac{\partial P(x,t)}{\partial x^2}\right]$$
where we assumed that \(\delta x\) remains small during the small time interval considered and expanded the distribution around \(x\). Rearranging yields
$$\frac{dP(x,t)}{dt} = - \frac{\langle\delta x\rangle_{\Delta t}}{\Delta t} \frac{\partial P(x,t)}{\partial x} + \frac{\langle \delta x^2\rangle_{\Delta t}}{2\Delta t}\frac{\partial P(x,t)}{\partial x^2}$$.
The coefficient \(v=\frac{\langle\delta x\rangle_{\Delta t}}{\Delta t}\) has the interpretation of a velocity: average displacement within time \(\Delta t\) divided by that time. The other coefficient has units \([displacement^2]/[time]\). We have seen above that mean squared displacement scales linearly in time in a simple discrete model. This holds more generally and we can define a time independent diffusion coefficient:
$$ \lim_{\Delta t \to 0} \frac{\langle \delta x^2\rangle_{\Delta t}}{2\Delta t} = D $$
The diffusion equation then takes the form
$$\frac{\partial P(x,t)}{\partial t} = - v\frac{\partial P(x,t)}{\partial x} + D\frac{\partial P(x,t)}{\partial x^2}$$.
Green's function of the diffusion equation
Depending on the initial and boundary conditions, the difusion equation admits different solutions. On important situation is the diffusion of particles that are initially localized at a point \(x=0\) and spread via diffusion.
$$ P(x,t) = \frac{1}{\sqrt{4\pi Dt}}e^{-\frac{(x-vt)^2}{4Dt}} $$
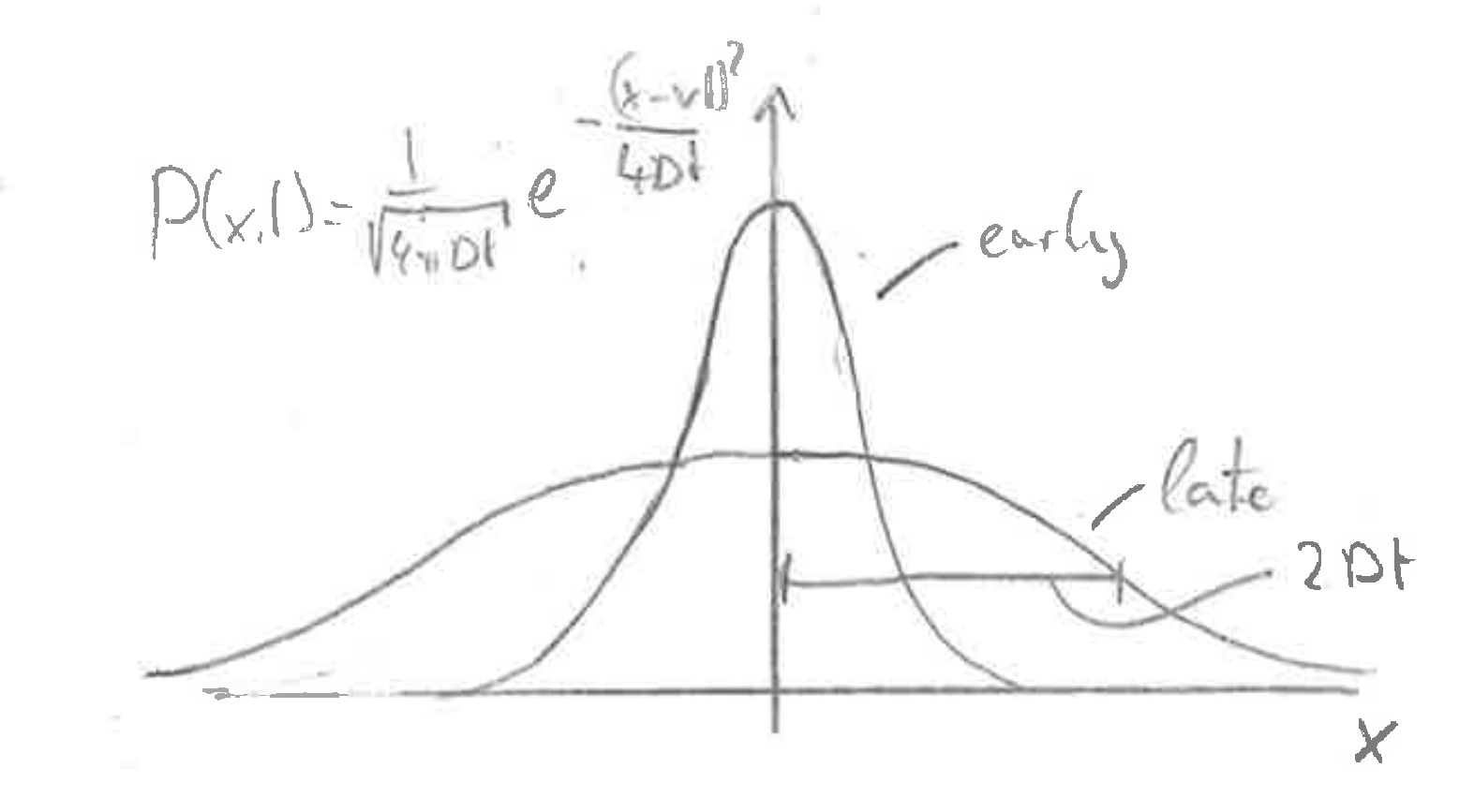
Verify that this is a solution!
Fluxes and boundary conditions
Whenever the distribution \(P(x,t)\) is inhomogenous, there is a net flux of particles. This is most readily seen by rewriting the diffusion equation as
$$ \frac{\partial P(x,t)}{\partial t} = -\frac{\partial}{\partial x}\left[ v P(x,t) - D\frac{\partial P(x,t)}{\partial x} \right] = - \frac{\partial}{\partial t} j(x,t) $$
where \(j(x,t)\) is the flux of particles. The parts of the flux have an intuitive interpretation: the term \(vP(x,t)\) describes how the density \(P(x,t)\) is moved by the advection velocity \(v\). The term \(D\frac{\partial P(x,t)}{\partial x}\) is the result of random diffusion: Whenever \(P(x,t)\) is falling, more particles remove from left to right than vice versa, resulting in a net flux towards the low density region. The expression for the flux is also known and Fick's law.
Fluxes are critical when we consider diffusion in a domain whose boundaries restrict fluxes. The most common boundary conditions are (i) no-flux boundaries (for example impermeable membranes), (ii) absorbing boundary conditions (for example a sticky surface), or (iii) constant flux boundary conditions where particles are injected at constant rate (for example a fly embryo with localized translation at one end of the embryo).
No flux boundary conditions
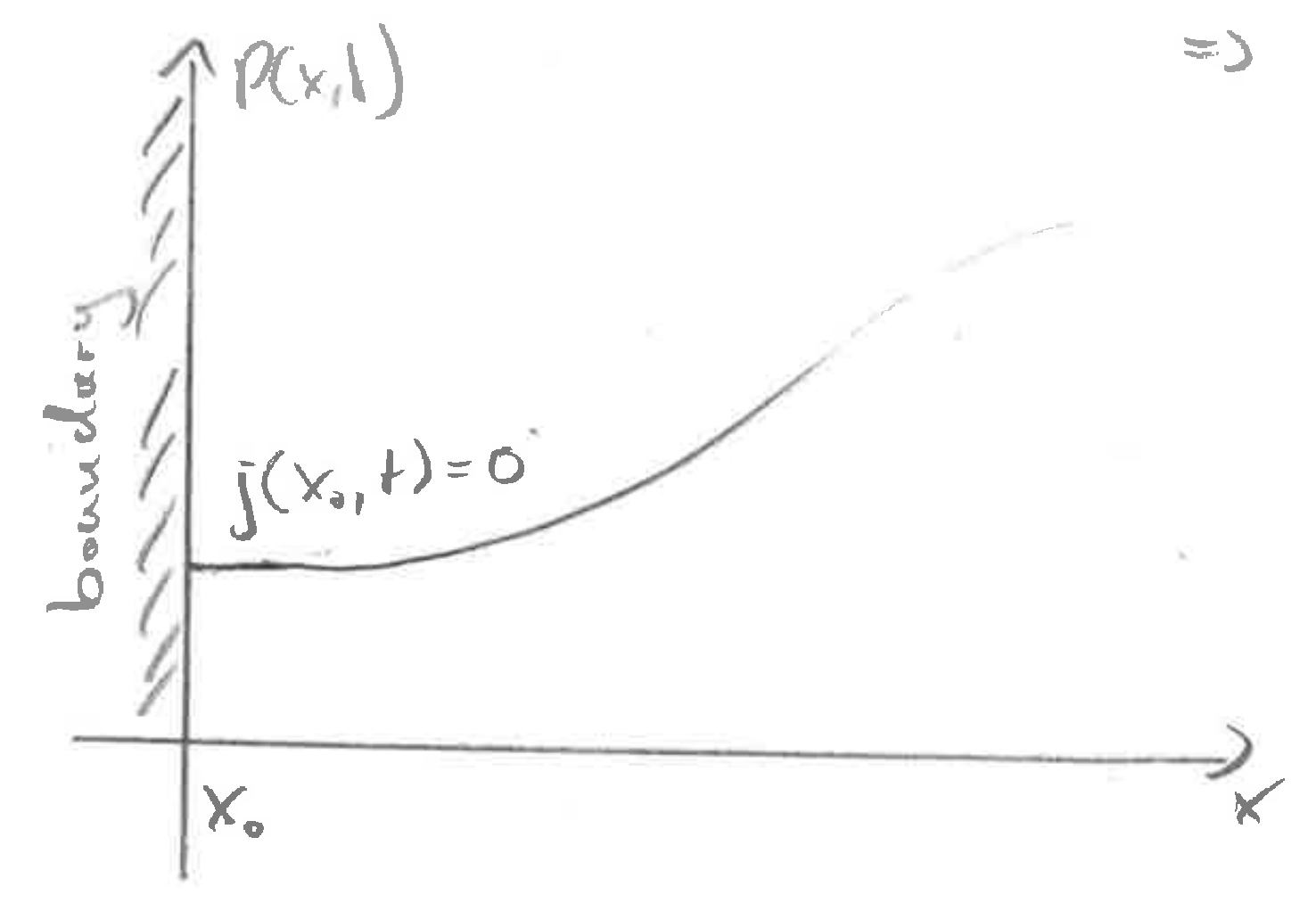At the boundary, the flux \(j(x,t)\) has to vanish. This is achieved if \(DP'(x,t) = vP\) (note that there is a \(P\) missing in the graph). In the particular care of \(v=0\), this corresponds to zero slope.
Absorbing boundary conditions
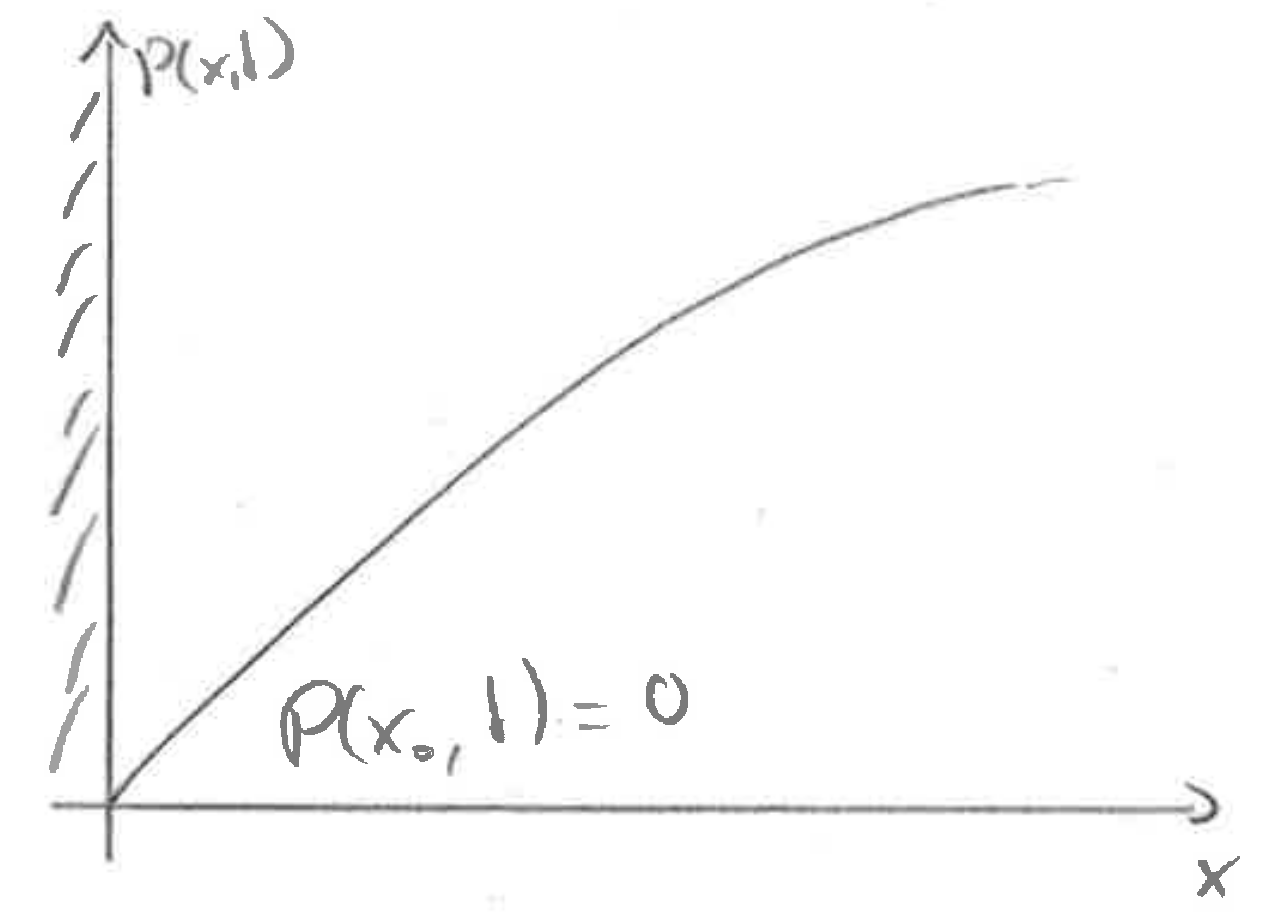At an absorbing boundary, the density at the boundary has to equal zero (unless \(D\to 0\) at the boundary). The probability flux at the boundary is the rate of absorbtion.
The method of mirror sources
The Gaussian solution above extends to infinity.
In a bounded domain, we need a different solution!
One common strategy is to use the method of mirror sources. What this does is best appreciated in a picture:
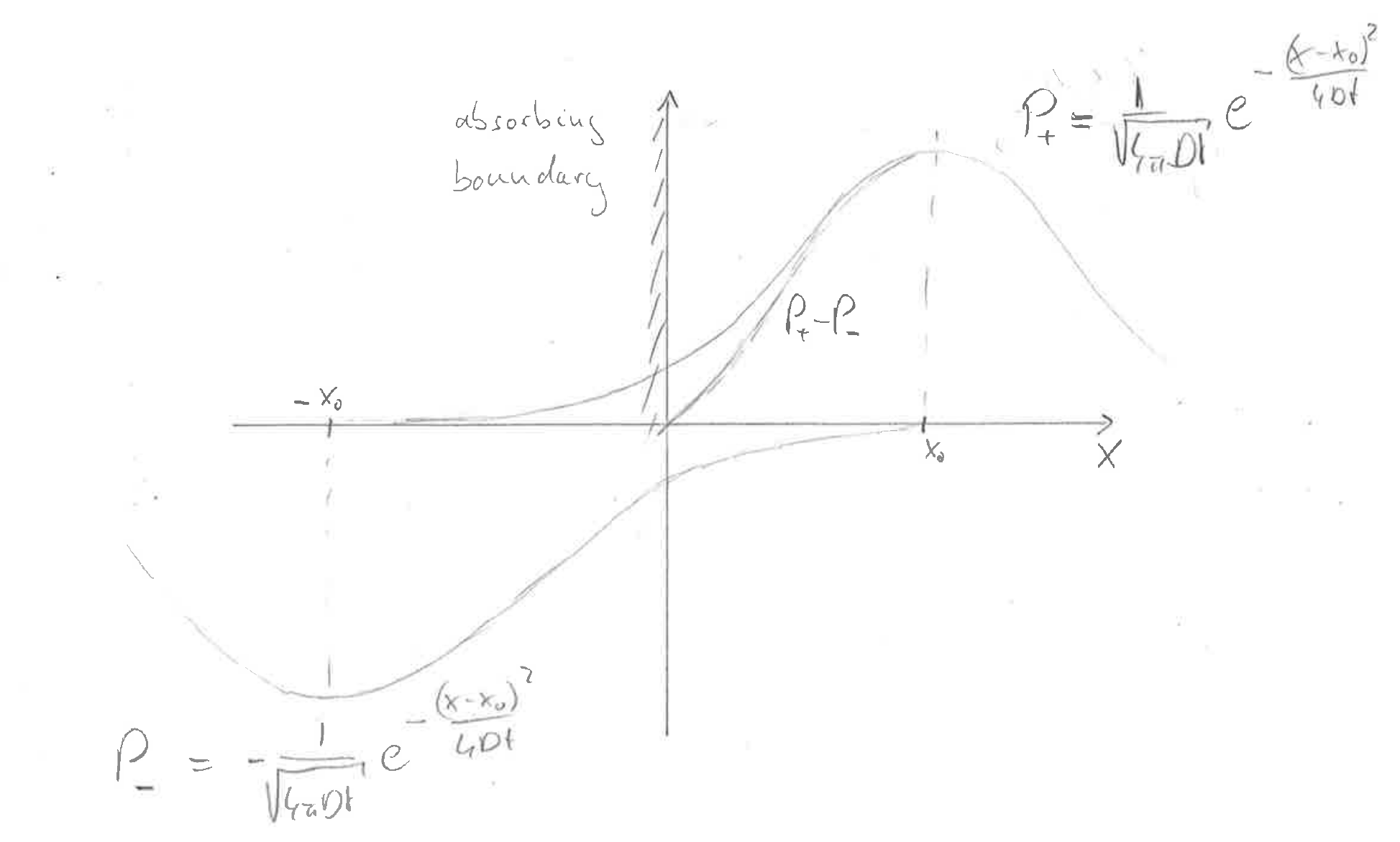Consider a source at position \(x_0\) and an absorbing boundary at \(x=0\).
If we place a negative source at position \(x=-x_0\) and add those two contributions, the sum will go through zero at \(x=0\) as required.
This superposition of different solutions works because the diffusion equation is a linear equation.
$$P(x,t) = \frac{1}{\sqrt{4\pi Dt}}\left[e^{-\frac{(x-x_0)^2}{4Dt}} - e^{-\frac{(x+x_0)^2}{4Dt}}\right]$$
Calculate (evaluate) the rate at which probability is lost. What is the \(\int_0^\infty dx P(x,t)\)?
The same trick can be used for reflecting boundary conditions: The two contributions from \(x=x_0\) and \(x=-x_0\) need to be added rather than subtracted.
$$P(x,t) = \frac{1}{\sqrt{4\pi Dt}}\left[e^{-\frac{(x-x_0)^2}{4Dt}} + e^{-\frac{(x+x_0)^2}{4Dt}}\right]$$
Does this also work for \(v\neq 0\)?
Script to plot and explore the solutions
Assignments
- Verify that \(P(x,n)\) solves the Master equation.
- Verify that \(P(x,t) = \frac{1}{\sqrt{4\pi Dt}}e^{-\frac{(x-vt)^2}{4Dt}}\) solves the diffusion equation.
- Calculate the rate at which probability is lost at an absorbing boundary at \(x=0\) if there was a unit mass at \(x=x_0\) at time 0. How much is left at time \(t\)? (numerical if necessary, make graphs of the solution.)