We have encountered a number of processes in past weeks that hydrolize ATP to drive irreversible reactions. In the case of the actin cytoskeleton, these irreversible reactions result in forces that drive cell motility. Here, we want to look more closely at proteins that explicitly convert chemical energy into mechanical work known as molecular motors. There are a number of different types of molecular motors, including
- cytoskeletical associated motors: myosin, dynein, kinesin
- ion pumps (ATP synthase can also run as a proton pump)
- rotary motors that drive flagella
- translocation: motors that import polymers or unfold proteins.
- DNA/RNA associated motors such as polymerases, helicases, viral packaging motors, chromatin condensation etc
Molecular motors have always fascinated biophysicists because of the direct link between biochemical reactions and mechanical work done by individual molecular machines. They devised many clever single molecule experiments to elucidate the properties of these machines.
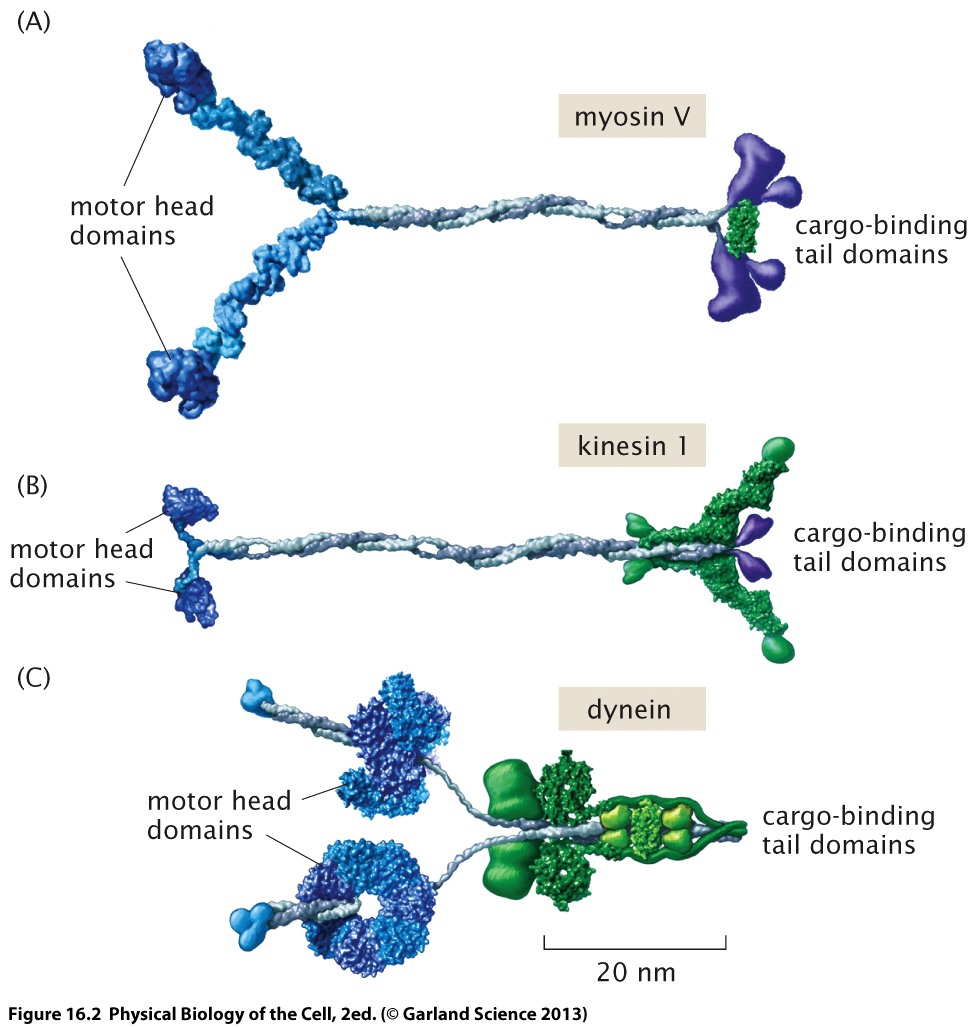
The following illustration shows sketches of the three most important "cargo" motors myosin V, kinesin, and dynein. Myosin uses actin, the other two microtubuli as substrates.
Assays to characterize motor activity and function
Actin sliding on myosin coated surfaces
Myosin motors immobilized on surfaces and propel labeled actin filaments
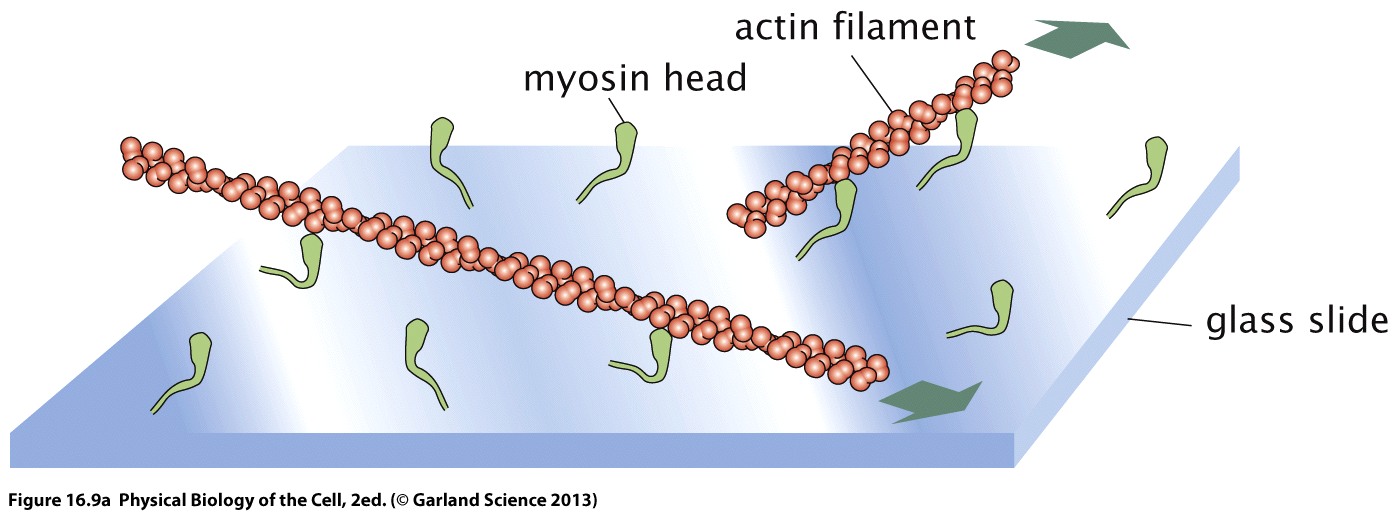
In presence of ATP, the myosin motors will start to push the actin filaments across the surface. This situation is partly analogous to myosin II in muscles, where many motors bind cooperatively to a filament. If the filaments are fluorescently labeled, the movement of the filaments can be observed in a microscope.
Single molecule techniques
The gliding assay discussed above is suitable to study bulk properties of many motors simultaneously. More sensitive technologies have been developed to study the dynamics of individual motor proteins.
How exactly these motors move along their substrates has been a long standing debate in molecular biophysics. Specifically, people disagreed on whether these motors moved via a "hand-over-hand" or "inch-worm" mechanism. These kind of questions are difficult to answer using crystallography or NMR or similar, but direct observation of single molecular motors resolved the controversy.
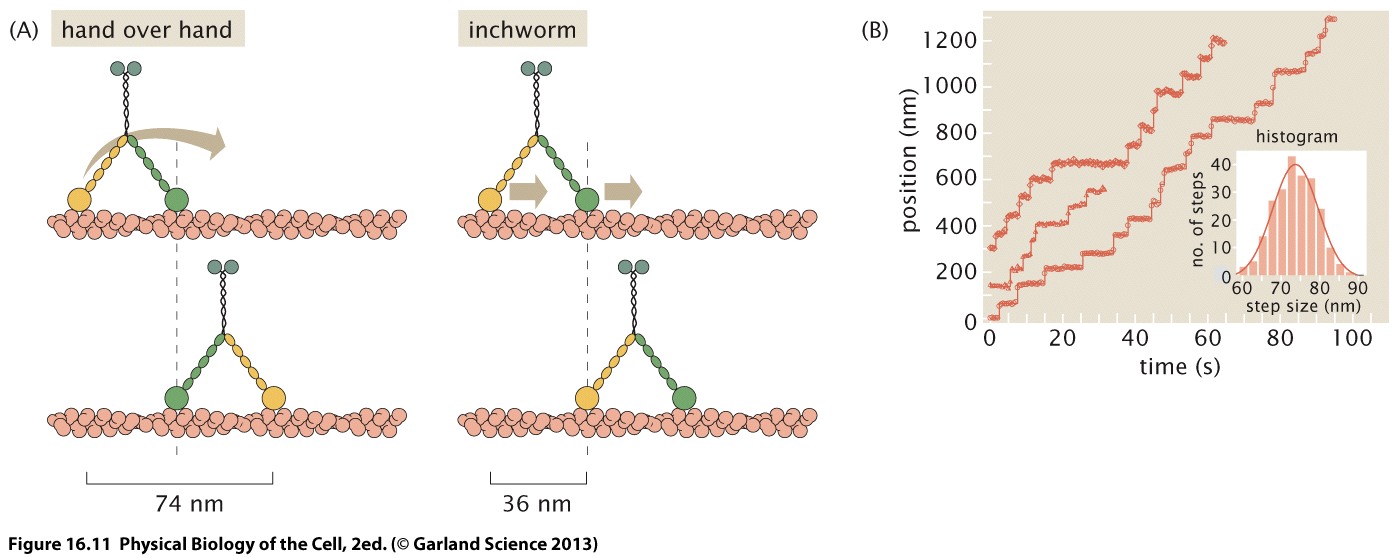
Yildiz et al labeled one of the two heads with a fluorescent label and directly observed the step-wise motion of the motor head. The head moved in steps of 70nm and the only compatible mode with this step size is the hand-over-hand mode. Similar experiments have been performed for kinesin. Note that the localization of the fluorophore in these experiments is much tighter than the diffraction limit. This tight localization works via a similar mechanism as PALM or STORM. Repeated observations from a point source can be fit to the known point spread function. Given enough data, the center of the point spread function can be fit to nm accuracy.
Observing rotary motors
Another fascinating class of molecular motors are rotary motors with their most prominent examples bacterial flagellum and the proton pump/ATP synthase.
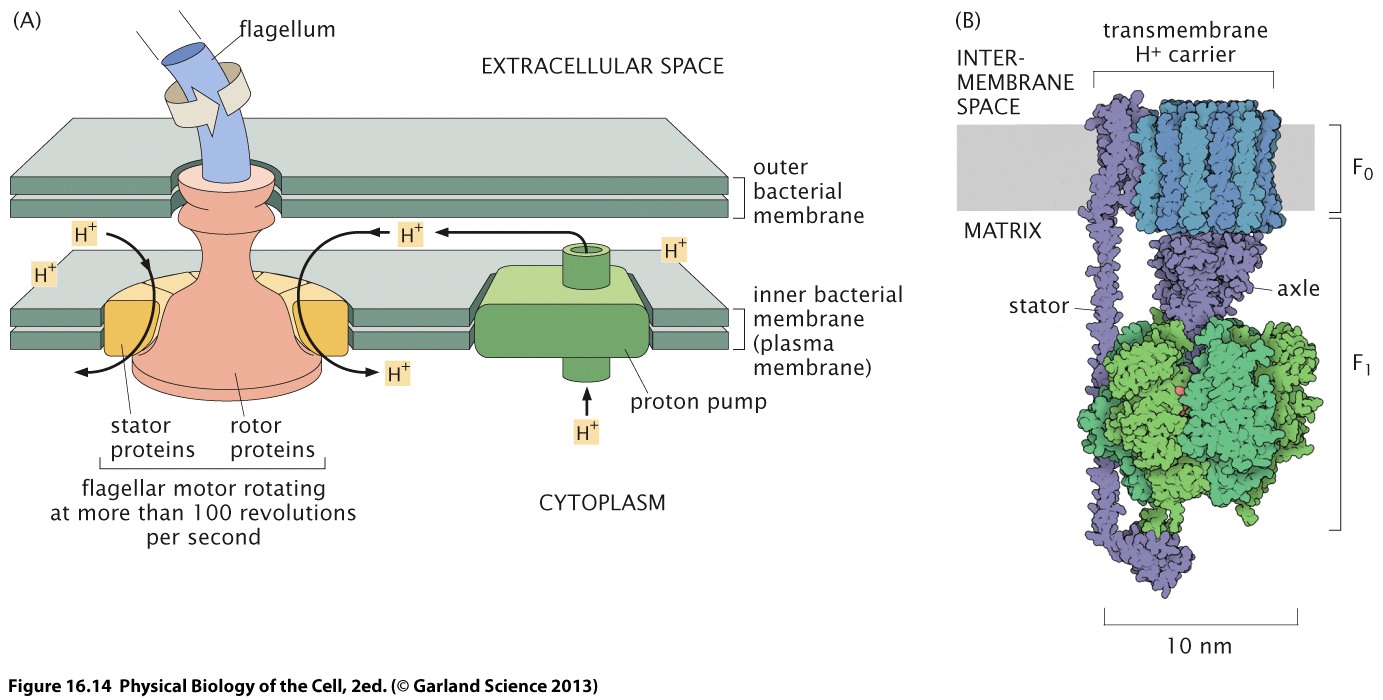
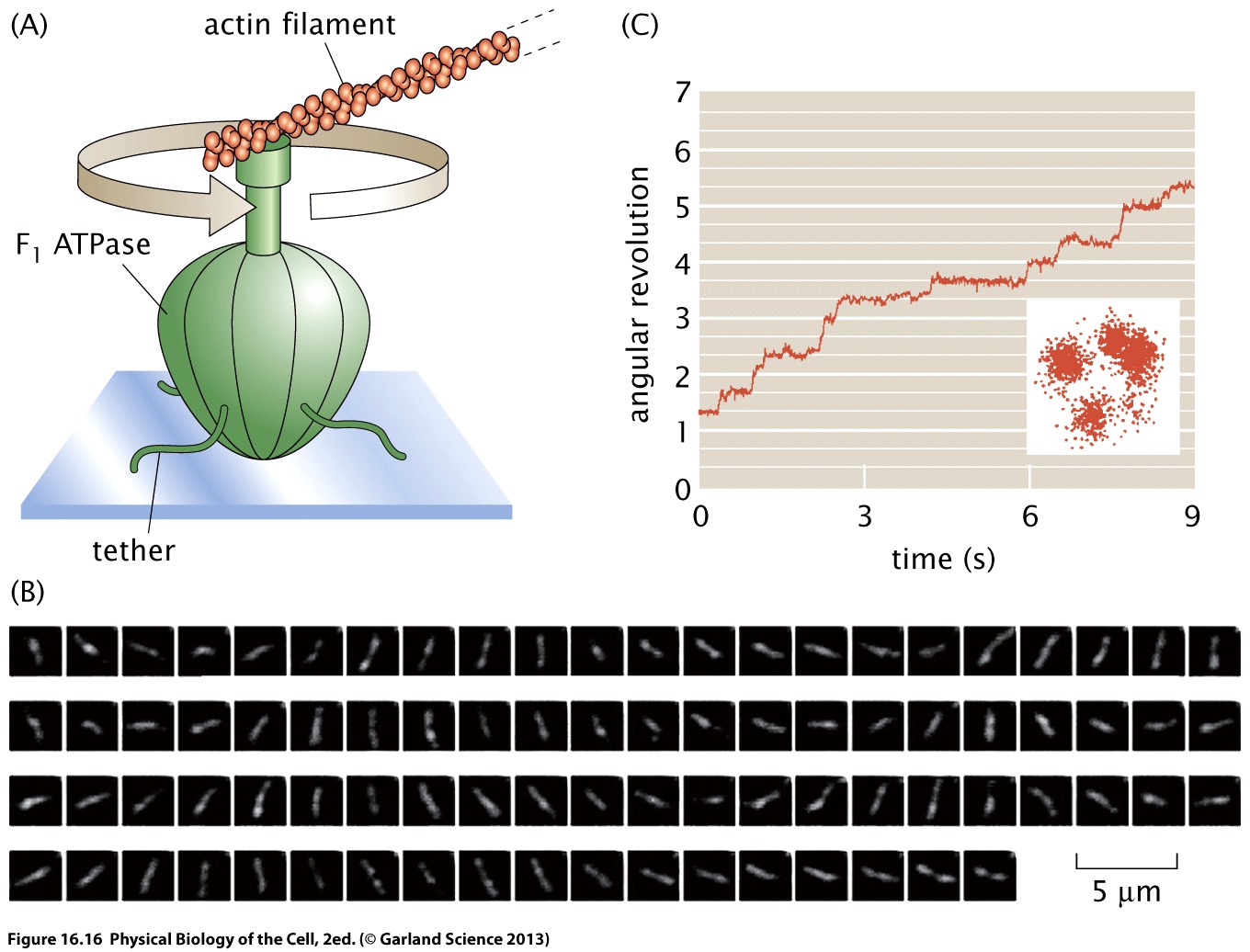
Noji et al figured out a way to observe the dynamics of single ATP synthase already more than 20 years ago. They attached a fluorescently labeled actin filament to the motor and could directly image the motion of the filament. This demonstrated clearly that the motor rotors in steps 120 degrees.
Response of motors to load
The experiments above observed motors in absence of load. A central task of the motor, however, is to perform work and work is performed through motion under load.
A sensitive technique to measure load and exert force are optical tweezers A bead can be positioned by a focused laser beam. The bead diffracts light and light diffraction generates a restoring force. At the same time, the position of the bead relative to the center of the beam can be determined via the refraction pattern.
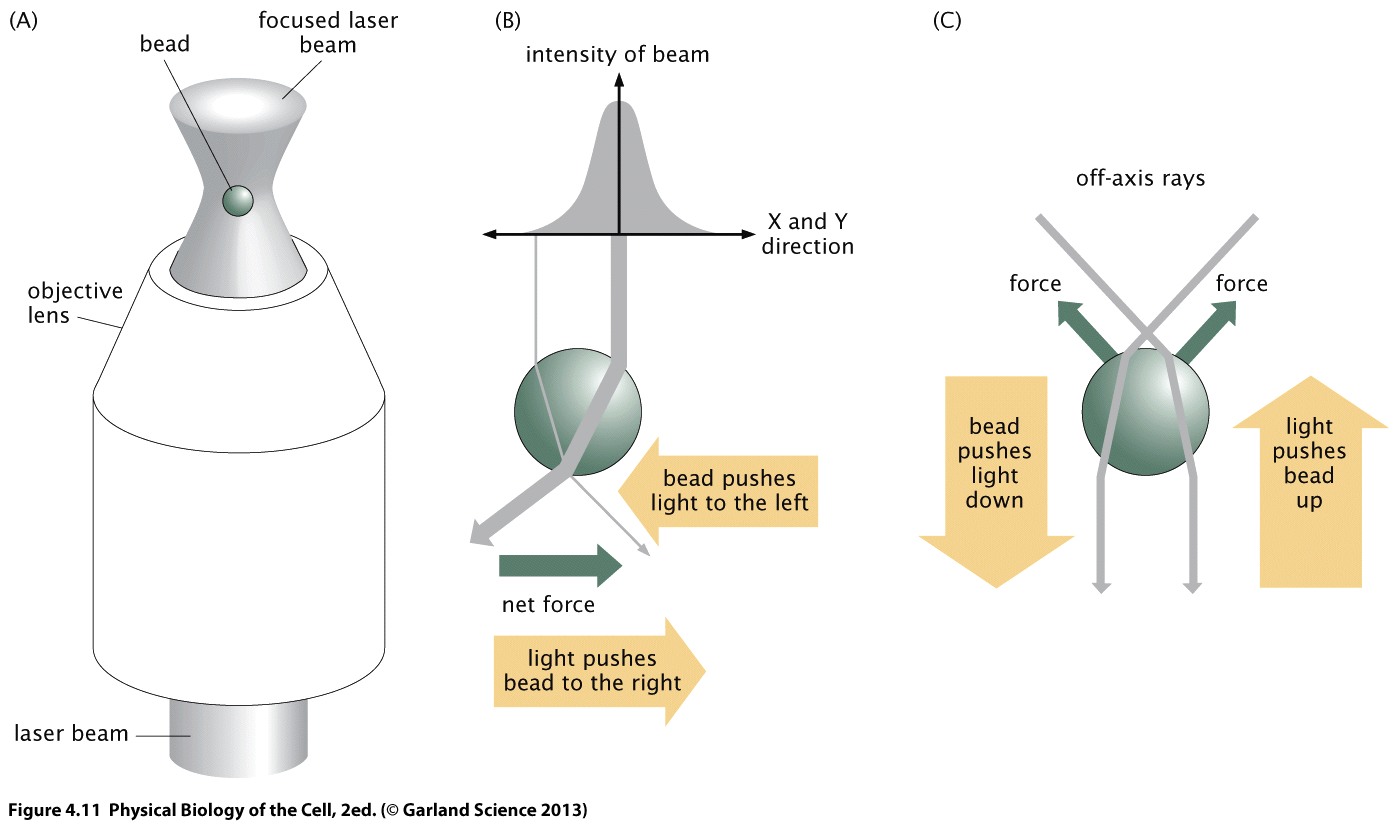
The beads can be functionialized in different ways and attached to molecular motors (via linkers), pieces of DNA etc.
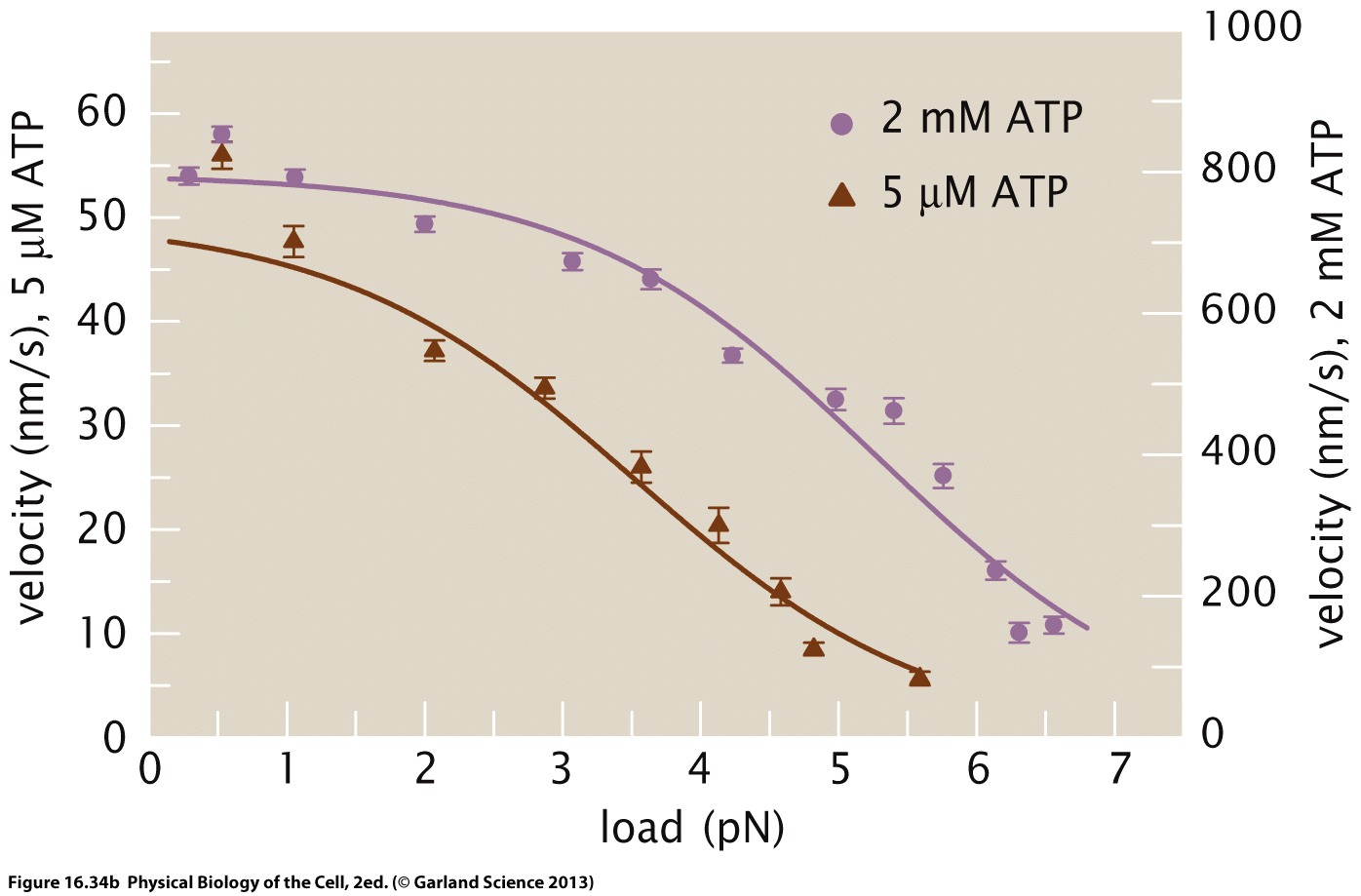
The figure below shows the load dependence of a kinesin molecular motor at different ATP concentrations. With increasing force, the velocity of the motor decreases until it hits zero at around 5-8pN. This stall force also seems to depend on the ATP concentration. The latter, however, mostly seems to affect the speed.
Detailed single molecule experiments have shown that the position of motors fluctuates and moves forward and (sometimes) backward on the microtubule. The higher the load, the more frequently the motor moves backward. Let's try to understand this behavior using a simple quantitative model in which the walker moves forward with rate \(k^x\) and backward with rate \(k^-\). The distribution of the walker along the track then obeys the equation
$$\frac{P(n,t)}{dt} = -(k^+ + k^-)P(n,t) + k^+P(n-1,t) + k^-P(n+1,t)$$
This equation should be familiar with the Master equation for random walks we studied earlier. This master equation can be transformed into a diffusion equation by realizing that the right hand side can be decomposed into a discrete first and second derivative.
$$\frac{P(n,t)}{dt} = \frac{k^+ + k^-}{2}\left[P(n-1,t) - 2P(n,t) + P(n+1,t)\right] + \frac{k^+ - k^-}{2}\left[P(n-1,t)- P(n+1,t)\right]$$
Hence the Master equation is equivalent to a diffusion equation with velocity and diffusion coefficient
$$V = a(k^+ - k^-) \quad\mathrm{and}\quad D = a^2\frac{k^+ + k^-}{2}$$
Now both the \(k^+\) and the \(k^-\) rate could depend on the applied force. For the same reasons we have encountered several times before, the dependence of rates on the applied force will generally be of Boltzmann form. If for example the \(k^+\) is the only rate that is force dependent, we expect
$$k^+ = k_0 e^{-aF/kT} $$
The length scale \(a\) here is the distance between binding sites on the track, which in the case of actin or microtubule filaments will be an integer multiple of the helical pitch. Whether the load is mostly affecting the forward or backward rate has measurable consequence: If the force is affecting the backward rate, the velocity responds little to force until the force approaches the stall force, beyond which the motor is rapidly going backwards. In the opposite case, the velocity is sensitive to load up to the stall force and has lower sensitive at large super stall-force loads. Experiments suggest that a load largely affects the backward rate. This is seen in the graph below, that illustrates the velocity dependence for the cases where the force affects \(k^+\)(A) and \(k^-\) (B) and shows experimental data by Gebhardt et al.
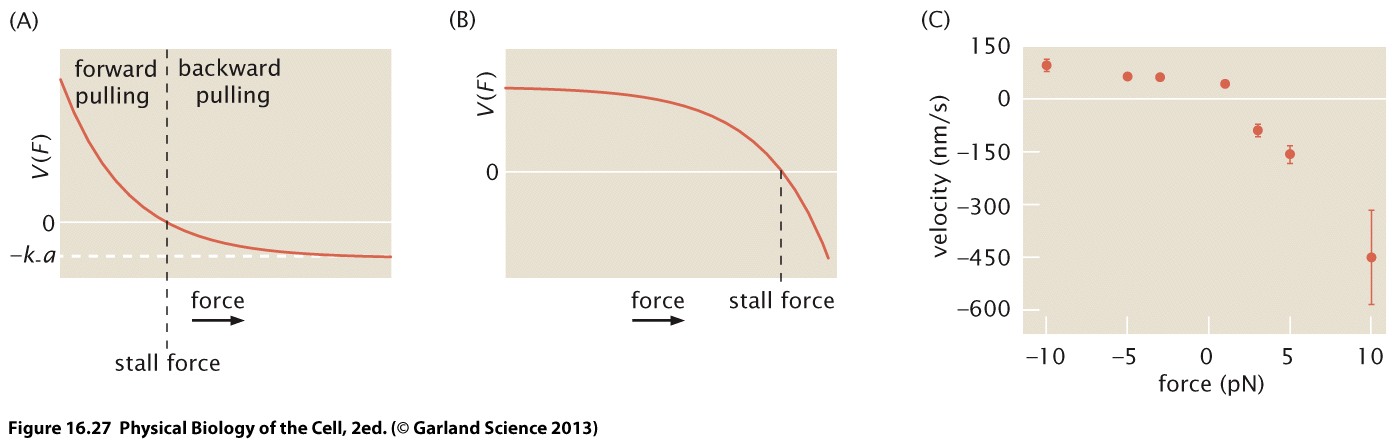
This simple model of a biased random walker captures some of the qualitative behavior, but misses a crucial part of physical reality: How does the walker know that left and right are different. Without internal states that are coupled ATP hydrolysis, no directed motion should be possible.
Assignments
- What is the drag force of a 100nm vesicle when moving at a typical molecular motor velocity? (use the viscosity of the cytosol and look up motor speeds)
- What is the distance beyond which directed transport by a molecular motor is faster than diffusion for (i) a typical protein, (ii) a 1kb mRNA, (iii) a 100nm vesicle?