Shifts in concentrations or modulation of interaction strength can result in sudden instability of a solution and separation into multiple liquid phases as we discussed earlier for the case of P-granules in early C. elegans embryos. In biological systems, such phase separation is often mediated by multivalent low affinity interactions between constituents, for example mediated by RNA/protein complexes. Similar phase separation can happen in membranes and such phase separation plays important roles in signaling.
Properties of lipid bilayers
Lipid bilayers from spontanously from amphiphilic lipids in solution. Individual lipid molecules arrange themselves such that the hydrophilic heads face the aqueous phase, while the hydrophopic tails touch each other. A large number of genometric conformations are possible depending on the type of liquid, the liquid mix, and their concentration.
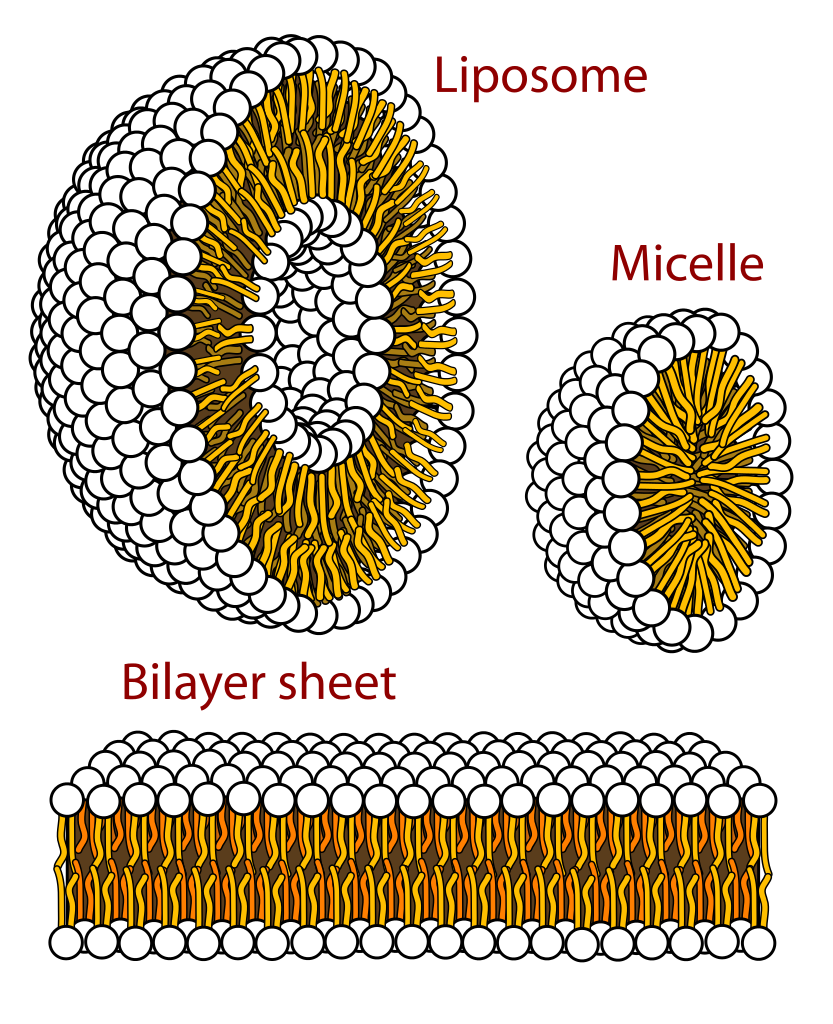
Mariana Ruiz Villarreal, wikipedia.org
These lipid bilayers are dynamic and represent a two dimensional fluid rather than a stiff sheet. Individual lipid molecules diffuse within the membrane and the membrane will respond to shear stress by flow. While dynamic and fluid within the sheet, individual lipids face a high energy barrier when flipping from one sheet to the next or leaving the membrane.
Lipid bilayers tend to have a bending stiffness and small vesicles tend to assume a shape that minimizes curvature. This stiffness is a result of finite thickness of the membrane. When the membrane is bent, spacing between the heads increases while the tails are pushed together.
Domain formation in lipid bilayers
Similar mechanisms that lead to phase separation in three dimensional liquids also generate domains in two dimensional membranes. This requires that the membrane is made from different types of lipids or has proteins embedded in the membrane. Attraction between molecules is not necessarily due to direct interaction between them, but can be mediated by distortion of the membrane.
 by Artur Jan Fijałkowski, wikipedia.org
by Artur Jan Fijałkowski, wikipedia.org
Such domain structures, also known as lipid rafts, often contain higher concentrations of cholestrol and particular kinds of lipids. The precise nature of lipid rafts and what molecular process is ultimately responsible for receptor clustering in membranes is still being debated. But long range interactions between lipids, proteins, and cholesterol with a two dimensional sheet is certainly a mechanisms that can lead to domain formation. Such tendencies can be redundantly reinforced by other interactions between receptors in the cytosol.
Membrane protein cross-linking
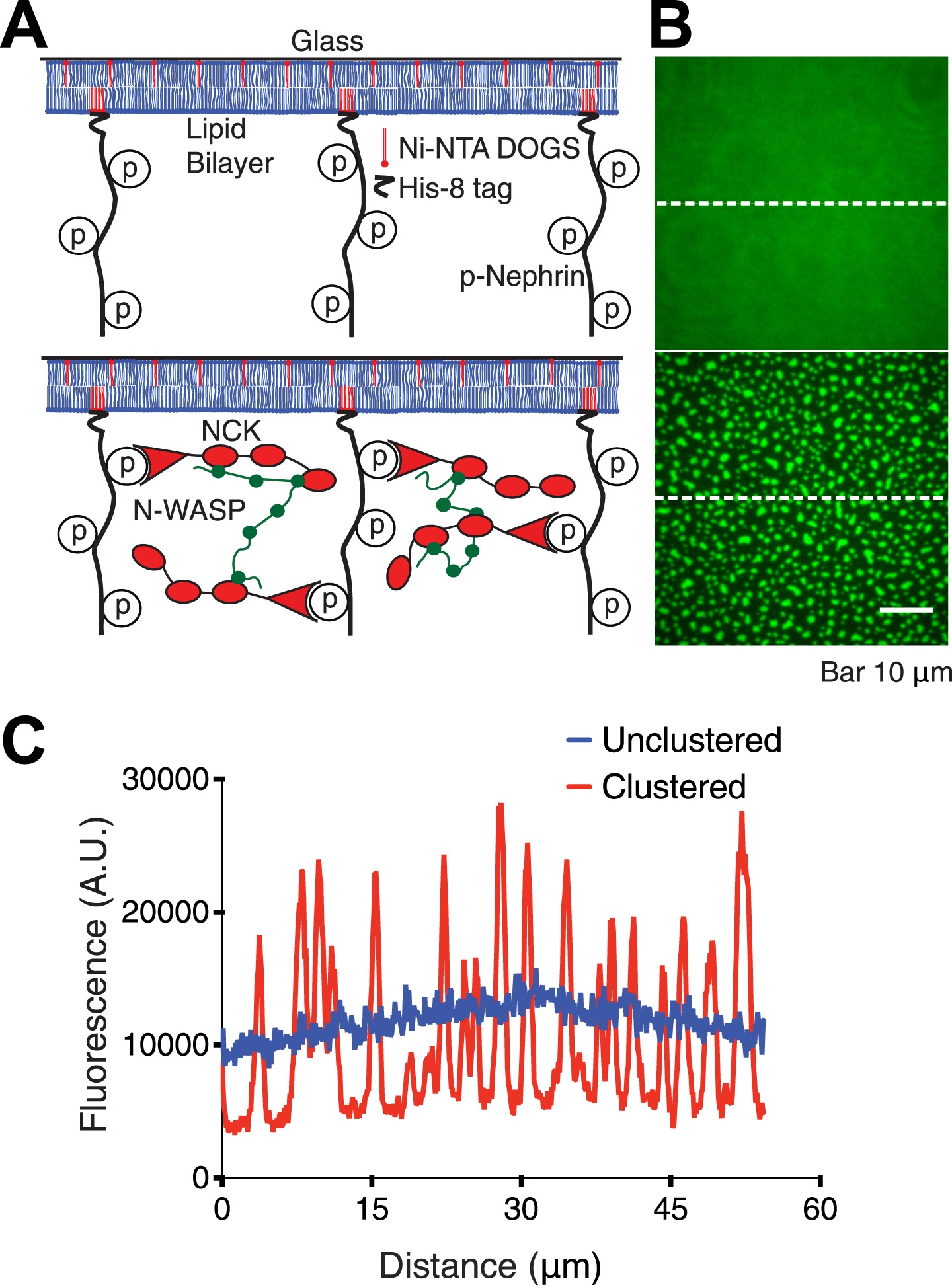
Percolation and gelation transitions
The phenomenon of clustering observed among membrane proteins is qualitatively similar to sol-gel transitions. Consider a polymer melt (a dense solution of polymers) and start adding cross-links between the polymers. With increasing number of cross-links, the system will go from a liquid to a gel which resists shear force. These cross-links could be covalent bonds, base-pairings, protein-crosslinks etc. Examples of this process abound for example in industrial applications or cooking.
Such a sol-gel transition has very intruiging features: The properties of the material change suddenly at a well defined density of cross-links. In the vicinity of the transition, the systems exhibits a number of universal properties that do not depend on the microscopic features of the system. The simplest mathematical model to appreciate this behavior is percolation on a so called Bethe lattice. Assume that each molecule \(z\) potential neighbors and that each pair of neigbors is cross-linked with probability \(p\). Furthermore, assume that there are no loops in the graph, i.e. that none of your neighbors are connected to each other (this is a strong approximation, but it will make the calculation is lot simpler). Let's call the probability that the molecule is not connected to the infinite connected component via a particular link \(Q = 1-P\). For the monomer not to be connected to infinite component via a particular link is
$$ Q = (1-p) + pQ^{z-1}$$
The first term accounts for the bond not being formed, while the second term corresponds to the bond being in place but none of the \(z-1\) other neighbors making a connection to the infinite component. Our monomer in question has \(z\) neighbors. Hence its probability not to be connected is \(P = Q^{z}\).
What solutions does the above equation have? For \(z=2\), it is clear that the only solution is \(Q=1\) unless \(p=1\). This is intuitively clear: there is no possibilty of making an infinite component with stochastically linking neighbors in one dimension. But for any \(z>2\), there is a non-trivial solution.
Consider \(z=3\) first. In this case, we are left with a quadratic equation for \(Q\)
$$ Q = (1-p) + pQ^2 \quad \Rightarrow\quad Q = \frac{1}{2p} \pm \sqrt{\frac{1}{4p^2} - \frac{1-p}{p}} = 1, \frac{1-p}{p}$$
The interesting solution is \(P = Q^3 = \left(\frac{1-p}{p}\right)^3\). This is larger than 1 for \(p<1/2\), which is obviously non-sensical. Put for larger \(p\), this solution is relevant. At \(p_c=0.5\), the fraction of monomers that are part of the giant component goes from strictly zero to a positive value and increases a \(p\) increases. In this simple model, the critical point is in fact always at \(p_c = \frac{1}{z-1}\).
Excurs: High througput sequencing technologies
Sequencing has undergone a revolution in recent years. The cost have fallen by orders of magnitude and throughput as increased to levels that were unimaginable just a few years ago. The chart below gives an impression of the development of the different technologies.

Notably, we have gone from about 1kb low throughput Sanger sequencing via high throughput short reads (~36bp) to now super high throughput medium length reads (~150bp). A few technologies (PacBio, nanopore) are pushing for much longer reads in excess of 10kb with increasing throughput. The cost for (re-)sequencing a human genome has also dropped precipitously to the point where preparation and analysis of the data are more costly than the sequencing itself.

The market leader is undoubtedly Illumina. Illumina uses an extremely scalable approach where individual short pieces of DNA are locally amplified in small clusters using a mechanism called bridge amplification.

DMLapato, wikipedia.org
A single flow cell of an illumina sequencer contains 100s of millions of such clusters at a density of around \(10^6/mm^2\). During sequencing, fluoresenctly labeled nucleotides are incorporated and the colorful clusters imaged using a sensitive camera. The sequence of colors can then be translated to sequence and Illumina sequencers achieve an accuracy better than 1/1000.

Image: EBI
The more recent long read technologies sequence individual molecules rather than clusters of identical molecules. This necessarily means much weaker signals and higher error rates.
Assignments
-
Solve for the gel fraction in the Bethe model with \(z=4\). There is a closed form solution for polynomial equation of third order, but its probably more straightforward to solve this numerically.
-
Play a bit with a percolation problem in 2D. There is a nice animation provided by Michael Toth. For a sufficiently large lattice, the giant spanning cluster suddenly appears as more and more squares are filled.