One often encounters the problem of a branching process in a changing environment. Let's assume that the environment is changing such that birth rates behave as $$ b = 1 + x - vt $$ while death rates are constant at \(d=1\). This situation is a typical model of a lineages in an adapting population where \(vt\) is the increasing mean fitness of the population. In order to survive, the lineage has to adapt and keep up with the increasing mean fitness. Let's assume a general mutation process with step site distribution \(\mu(s)\) and a total mutation rate \(\mu = \int ds \mu(s)\). One straightforward way to calculate the distribtion \(p(n,t|x)\) of the number of descendants \(n\) at time \(t\) given the lineages started at fitness \(x\) at time \(t=0\) is via a first step equation. A first step equation (similar to a backward Fokker-Planck equation) varies with respect to the initial condition and expresses \(p(n,t|x)\) as the whatever happens between \(t=0\) and \(t=\Delta t\) and \(p(n,t-\Delta t | x - v\Delta t)\). Importantly, at \(t=\Delta t\) the mean fitness of the population has increases by \(v\Delta t\) and the growth rate of the focal lineage had decreased. The first step equation then reads $$ p(n,t|x) = (1 - \Delta t (2+x+\mu))p(n,t-\Delta t|x-v\Delta t) + \Delta t \left[\delta(n=0) + (1+x)\sum_{n'=0}^n p(n', t|x)p(n-n', t|x) + \int ds \mu(s)(p(n,t|x-s) - p(n,t|x)) \right] $$ The first terms corresponds to nothing happening other than the clock advancing, while the terms in brackets correspond to death, division, and mutation. Rearranging and approximating the mutation terms by a Taylor series in small mutations, we have $$ \dot{p}(n,t|x) + vp'(n,t|x) = -(2+x)p(n,t|x) + \delta(n=0) + (1+x)\sum_{n'=0}^n p(n', t|x)p(n-n', t|x) + \mu\langle s\rangle p'(n,t|x-s) + \frac{\mu \langle s^2\rangle}{2}p''(n,t|x) $$ To clean this up a little, let's define \(\sigma^2 = v - \mu \langle s \rangle\) and \(D = \frac{\mu \langle s^2 \rangle}{2}\). $$ \dot{p}(n,t|x) = -(2+x)p(n,t|x) + \delta(n=0) + (1+x)\sum_{n'=0}^n p(n', t|x)p(n-n', t|x) - \sigma^2 p'(n,t|x-s) + Dp''(n,t|x) $$ Next, we consider the generating function \(\hat{p}(\lambda, t|x) = \sum_{n=0}^\infty \lambda^n p(n,t|x)\). Multiplying the equation by \(\lambda^n\) and summing over \(n\) will factorize the convolution and turn the \(\delta(n=0)\) into 1: $$ \dot{\hat{p}}(\lambda,t|x) = -(2+x)\hat{p} + 1 + (1+x)\hat{p}^2 - \sigma^2 \hat{p}' + D\hat{p}'' $$ This equation can be further simplified by substituting \(\phi = 1 -\hat{p}\): $$ \dot{\phi}(\lambda,t|x) = (2+x)(1-\phi) - 1 - (1+x)(1-\phi)^2 - \sigma^2 phi' + D\phi'' $$ which after some rearrangment simplifies to $$ \dot{\phi}(\lambda,t|x) = x\phi - \sigma^2 \phi' + D\phi'' - (1+x)\phi^2 $$ The initial condition is \(\phi(\lambda, t=0|x)= 1-\sum_n \lambda^n p(n,t=0|x)=1-\lambda\) when starting from one individual at fitness \(x\).
The mean number of descendents
The mean \(\langle n\rangle(t|x) = -\frac{d\phi}{d\lambda}(\lambda=1)\). We can therefore derive the following equation for the mean $$ \dot{\langle n\rangle}(t|x) = x\langle n\rangle - \sigma^2 \langle n\rangle' + D\langle n\rangle'' - 2(1+x)\phi|_{\lambda=1} \langle n\rangle $$ where the last term is identical zero since \(\phi==0\) if the initial condition is \(\lambda=1\) (all terms in the evolution equation for \(\phi\) vanish if \(\phi=0\)). This equation has the solution $$ \langle n\rangle(t,x) = e^{xt - \frac{\sigma^2t^2}{2} + \frac{Dt^3}{3}} $$ The clone initally starts growing but the growth rate is gradually declining due to increasing mean fitness. During this time, the clone is diversifying and develops into a small traveling wave of its own. Selection on the increasing diversity attenuates the decline in growth rate. Only when the initial fitness is \(>\frac{\sigma^4}{2D}\) is the growth rate always positive. This initial fitness corresponds to the positions of the most fit individuals in a traveling wave model.
Survival probability
The probability that there is at least one descendant at time \(t\) is $$ p_s = 1 - p(0,t|x) = 1 - \hat{p}(0,t|x) = \phi(0,x,t) $$ With initial condition \(\lambda=0, \phi=1\), the solution for \(\phi\) undergoes different characterisitic phases. At small times, \(\phi\) is flat and none of the derivatives are important. Furthermore, typical fitness differentials are small (\(|x|\ll 1\)) such that the initial dominant balance is \(\dot{\phi} = -\phi^2\) with solution $$ \phi(t|x) = \frac{1}{1+t} $$ Hence the branching process is initially insensitive to growth rate differences and behaves like a critical branching process. Only after \(t\sim 1/x\gg1\) is the selection term important. At large \(x\), the dominant balance shifts to \(x\phi = (1+x)\phi^2\) and therefore \(\phi = x/(1+x\). This is the same result as you would find for a standard super-critical branching process: The lineage needs to escape initial stochastic loss, but once established grows fast enough to outrun the adapting population. This dominant balance will remain valid above \(x_c = \frac{\sigma^4}{2D}\).
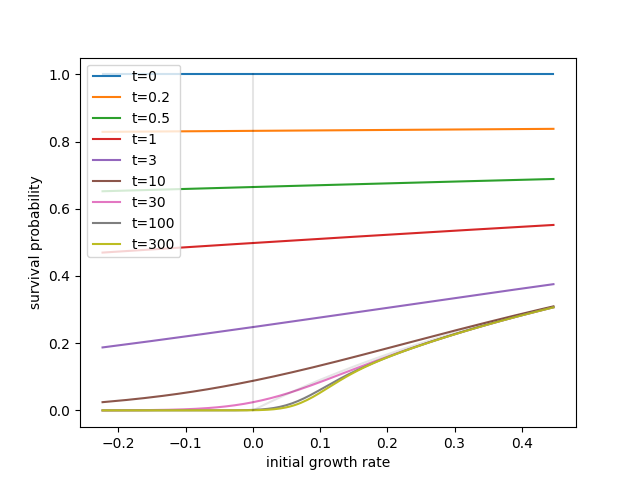
Below \(x_c\), the increasing mean fitness strongly reduces the fixation probability. Ignoring the \(\phi^2\) term, the remaining linear equation at steady state $$ 0 = x\phi - \sigma^2 \phi' + D\phi'' $$ Has a solution in terms of Airy functions. The relevant solution goes to zero at large negative \(x\) and crosses over to the linear
The script below solves for the survival probability at different times (via a very simple minded forward Euler solution of the differential equation).
import numpy as np
import matplotlib.pyplot as plt
def dphidt(phi,x,D,v):
dphidx = np.zeros_like(phi)
dphidx[1:-1] = (phi[2:] - phi[:-2])/(x[2:] - x[:-2])
dphidx[0] = (phi[1] - phi[0])/(x[1] - x[0])
dphidx[-1] = (phi[-1] - phi[-2])/(x[-1] - x[-2])
dphidx2 = np.zeros_like(phi)
dphidx2[1:-1] = 0.25*(phi[2:] - 2*phi[1:-1] + phi[:-2])/(x[2:] - x[:-2])**2
return x*phi - v*dphidx + D*dphidx2 - (1+x)*phi**2
D = 0.0005
v = 0.002
dt = 0.01
tp = [0,.2,0.5,1,3,10,30,100,300]
x=np.linspace(-5*np.sqrt(v), 10*np.sqrt(v), 151)
phi = np.ones_like(x)
i=0
t=0
plt.figure()
while True:
if t>=tp[i]:
plt.plot(x, phi, label='t='+str(tp[i]))
i+=1
if (i==len(tp)):
break
phi+= dt*dphidt(phi, x, D, v)
t+=dt
plt.legend(loc=2)
plt.plot([0,0], [0, 1], c='k', alpha=0.1)
plt.plot(x[x>0], (x/(1+x))[x>0], c='k', alpha=0.1)
plt.ylabel('survival probability')
plt.xlabel('initial growth rate')