Two studies of the influenza virus transmission bottleneck size (the typical number of viral genomes that contribute to a new infection) have come to very different conclusions: Poon et al, 2014 estimated a bottle neck size of the order of 100, while McCrone et al, 2017 estimate a typical bottleneck of size one. The differences between those studies likely have to do with the setting in which transmission happened, but this is not the focus of this post. Instead, I'd like to discuss whether the transmission bottleneck size actually matters for the way we think about influenza virus evolution.
Population bottlenecks are typically associated with inefficient selection since each bottleneck down-samples the population and likely prunes rare beneficial variants from the population. The situation in influenza virus populations is, however, very different from the classical population genetics scenario:
- 100s of millions of humans are infected every year
- the viral mutation rate is much larger than the inverse populations size (both the within host viral population as well as the number of infected hosts)
While bottlenecks will surely decrease the rate at which beneficial mutations spread, we will see that even tiny transmission bottlenecks allow for efficient selection of antigenic escape mutations.
The dynamics of mutations within hosts
The typical influenza virus infection last a few days with several tens of viral replication cycles (~6h). The peak viral load (very roughly \(10^6\)/ml, \(10^8\) total) is observed after about two days or eight replication cycles, suggesting a replication ratio of about \(R_0 = 10\) and an exponential growth rate of \(\alpha\approx 2\) per cycle (again very rough, Baccam et al estimate \(R_0\) to be a little higher, Hadjichrysanthou et al estimate lower values).
Now consider a mutation that allows partial escape from preexisiting immunity. Viruses with this mutation will spread preferentially from one individual to the next (we'll consider this part below), but they are also likely beneficial within the host. Such mutations arise from the infecting clone with a mutation rate \(\mu \approx 2 \times 10^{-5}\) per cycle and we'll parameterize their effect on replication by a selection coefficient \(s\) (for every new infection by an original virus, mutants will produce on average \(1+s\)). The infecting virus population initially increases as \(n_0 = e^{\alpha t}\) and produces mutant virus rate \(\mu n_0\). The resulting mutant clones will then subsequently increase with rate \(\alpha+s\) and the fraction of mutant viruses at time \(\tau\) $$ f_m(\tau) = \frac{n_m}{n_0} = \frac{\int_{0}^\tau \mu e^{\alpha t}e^{(\alpha+s) (\tau-t)} dt}{e^{\alpha \tau}} = \frac{\mu}{s}\left[e^{s \tau}-1\right] $$ where \(\tau\) is measured in replication cycles. Substantial selection will happen if \(s\tau\gg 1\) which is the case as soon \(s\) exceeds a 10%. It is not typically observed that a mutation rises to frequencies of order one within hosts, but \(s\tau \sim 4\) would increase a variant frequency to 0.5% -- a big effect but still hardly detectable in sequencing data.
If, instead of arising by mutation from the original virus type, the mutant is initially present at frequency \(f_0\), the frequency at time \(\tau\) will be simply $$ f(\tau) = \frac{e^{s\tau}}{(f_0^{-1}-1)+e^{s\tau}} $$
Transmission
Most human influenza transmission is via droplets and these droplets contain many viruses. But many of these viruses are defunct or fail to contribute to the infection because they end up in the wrong place or fail to over-come host defenses. An antigenically novel mutant virus is likely preferentially transmitted. We will parameterize this effect by having making the probability to transmit proportional to \(1+fr\) where \(f\) is the frequency of the mutant. The initial frequency of mutant in the new infection is then binomially distributed with \(b\) trials and success probability \(f\).
The figure below shows the results of a simple simulation. As expected, large bottlenecks accelerate the spread of the mutant, but not dramatically so.
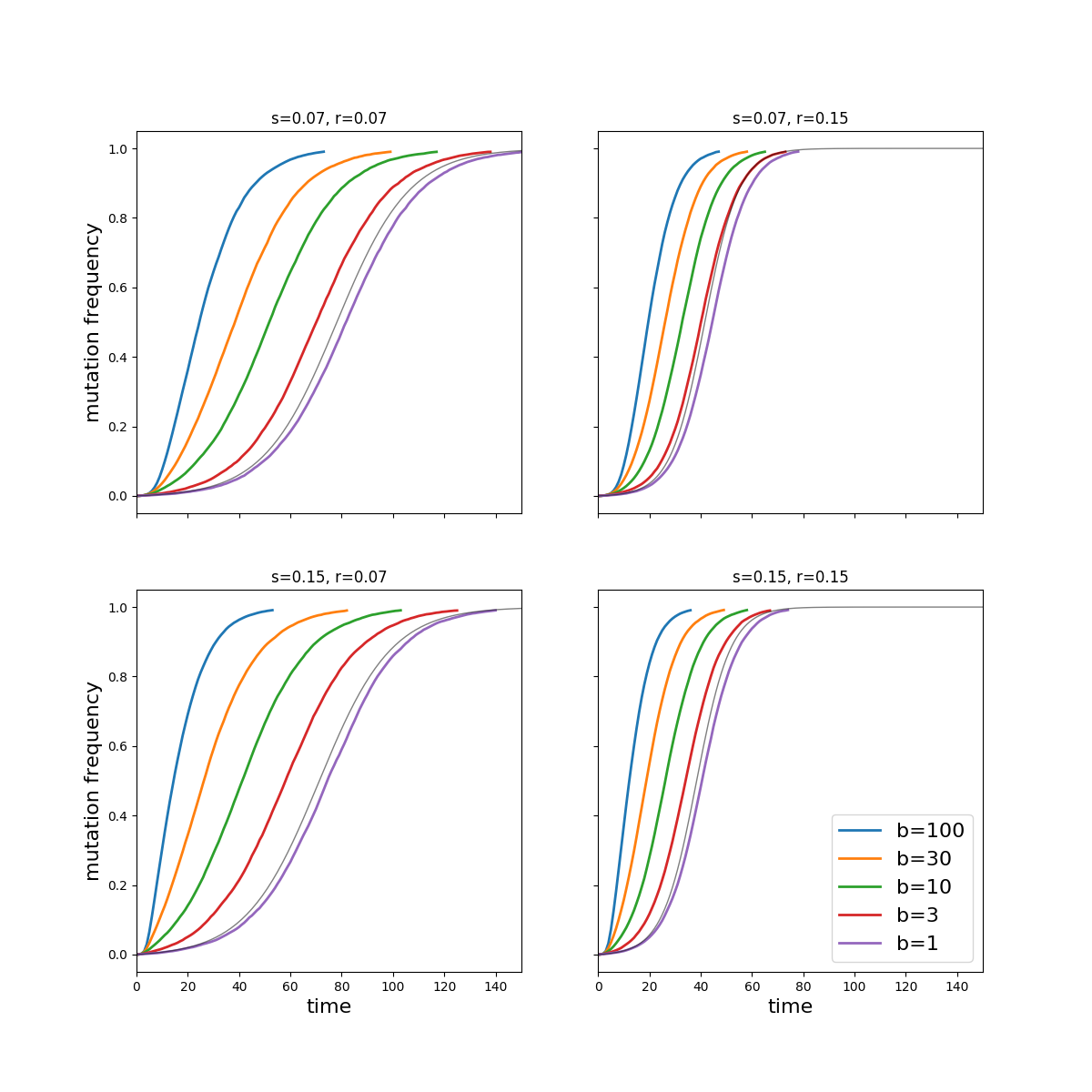
The effect of the bottleneck is pronounced if there is substantial within host selection (large \(s\)) and only a small effect on the transmission rate (small \(r\)), while the bottleneck size matters little if no strong selection is going on within (small \(s\), large \(r\)).
Asymptotic behavior for small bottlenecks
For very small bottlenecks as observed by McCrone et al variation is not transmitted and the within host amplification of mutations has the effect of an increased effective mutation rate given by $$ \mu_e = \frac{\mu}{s}\left[e^{s\tau}-1\right] $$ For \(s\tau\approx 3\), this will increase the mutation rate by a factor of 10. Beyond that, selection operates at the level of transmission and the mutants spread with a growth rate \(r\). An effective model based on this increased mutation rate and selection coefficient \(r\) describes the simulations for small bottlenecks well (grey lines in the figure).
For very large bottlenecks, selection operates continuously on each viral replication and the mutant enjoys an average growth rate of \(s + r/\tau\) per virus replication. This growth rate is only realized for bottleneck sizes on the order of the inverse mutation rate.
Summary
The rapid molecular evolution of seasonal influenza viruses depends much more strongly on the ability of the virus to evade pre-existing immunity by mutation than efficient transmission of minor variation.
- Even if the bottleneck is tiny, a variant will spread as long as it confers a benefit at transmission.
- Small bottlenecks slow down but don't prevent the spread of an antigenic escape variant. But the effect of bottlenecks is large when within host selection is strong compared to its effect on transmission.
- The dynamics when bottleneck are small is well described by a model with selection only at transmission. All within-host dynamics can be captured by an effective mutation rate.
The transmission bottleneck is important for all sorts of other aspects, including our ability to track transmission chains, complementation, etc. Please keep sequencing!
Updates
- Adam Kucharski pointed out that the effect of mutations on within host dynamics and transmission can go in opposite directions: Frise et al, Scientific Reports
- Daniel Weissman remarked that the way the simulation selects for transmission is purely on the basis of the fraction of mutant in the droplet and doesn't account for preferential infection by the mutant beyond the mutation frequency. This should be accounted for.
Thanks a lot for your feedback.
Code
The figure above was generated with this python script:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# set parameters
Nhost = 100000
mu = 2e-5
max_gen = 500
tau = 10
# set up four panel figure
plt.ion()
fs=16
fig, axs = plt.subplots(2,2, sharey=True, sharex=True, figsize=(12,12))
# loop over transmission effect r and within host effect s
for ri,r in enumerate([0.07, 0.15]):
for si, s in enumerate([0.07, 0.15]):
ax = axs[si,ri]
ax.set_title("s=%1.2f, r=%1.2f"%(s,r))
# loop over bottleneck b
for b in [100,30,10,3,1]:
fmut = np.zeros(Nhost)
tmp = np.zeros(Nhost)
mutation_frequency = [0]
while mutation_frequency[-1]<0.99:
# within host
ind = fmut==0
tmp[ind] = mu/s*(np.exp(s*tau)-1)
tmp[~ind] = fmut[~ind]*np.exp(s*tau)
fmut = tmp/(1-fmut+tmp) # normalize (logistic)
# transmission
success = []
while len(success)<Nhost:
# generate at least Nhost transmission with success probability 1+fr
ind = (1+fmut*r)>(1+r)*np.random.random(len(fmut))
success.extend(fmut[ind])
# shuffle transmissions and resample binomially
np.random.shuffle(success)
fmut = np.array(binom.rvs(b, success[:Nhost]), dtype=float)/b
# record overall mutation frequency
mutation_frequency.append(fmut.mean())
#plot mutation frequency trajectory
ax.plot(mutation_frequency, label='b=%d'%b, lw=2)
# plot the effective model for small bottlenecks
mu_e = mu/s*(np.exp(s*tau)-1)
t = np.arange(200)
x = mu_e/r*(np.exp(r*t)-1)
ax.plot(t, x/(np.exp(-mu_e*t)+x), c='k', lw=1, alpha=0.5)
if si==1:
ax.set_xlabel('time', fontsize=fs)
if ri==0:
ax.set_ylabel('mutation frequency', fontsize=fs)
if si and ri:
plt.legend(loc=4, fontsize=fs)
ax.set_xlim(0,170)