Thinking about cellular and biophysical processes is easier if one has a sense of the relevant scales. In fact, almost every statement about a quantity is only useful when compared to something else -- that is why we have units. Our day to day units (meters, kilogram, etc) are tailored to the world we live in and don't mean much at the microscopic scale. A very useful collection of important quantities is available at bionumbers.org by Rob Phillips and Ron Milo. Once we have identified the relevant scales and sizes, simple reasoning and comparing different scales can already give us quite detailed and robust insight into many cell biological properties.
How small are things?
The following table has (very) rough numbers for the different sizes involved
- \(3\times 10^{-10}\)m (0.3nm): height of one DNA base pair
- \(2\times 10^{-9}\)m (2nm): diameter of DNA, typical protein diameter
- \(2\times 10^{-8}\)m (20nm): bacteria phage
- \(10^{-7}\)m (0.1um): animal virus
- \(10^{-6}\)m (1um): bacterial cell
- \(2\times 10^{-6}\)m (2um): yeast cell nuclei
- \(10^{-5}\)m (10um): eukaryotic cell
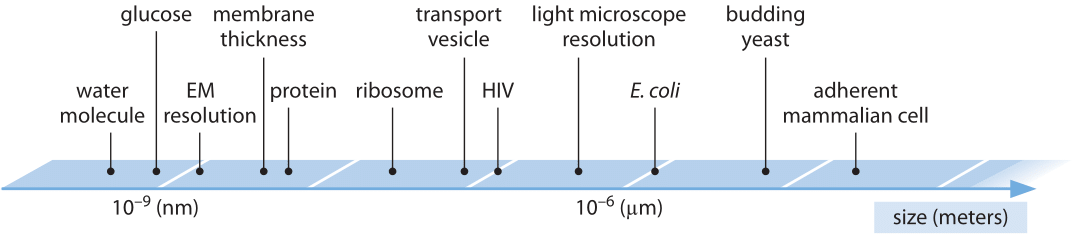The range of linear dimensions relevant in a cell from bionumbers.org.
With this huge range of linear dimensions, volume and mass vary over a much larger range still. It is useful to remember: One liter \(10^{-3}m^3\), one milliliter is a \(cm^3\) (the size of an eppendorf tube), one femto liter is \(\mu m^3\). One gram of water is roughly one ml. Using the length above (there is obviously a lot of variation between types).
- \(10^{-20}\)l: volume of a bacteria phage
- \(10^{-15}\)l (1fl): volume of a bacterial cell
- \(10^{-12}\)g (1pg): weight of a bacterial cell
- \(10^{-12}\)l (1pl): volume of a eukaryotic cell
Humans weigh roughly 100kg (100l volume) and most of "human stuff" is made from cells. Given they rough weight of a cell, we estimate \(10^{14}\) human cells in the human body. The true number is closer to \(10^{13}\), but this discrepancy is within the accuracy of our calculation. Furthermore, we immediately see that a comparable number of bacterial cells will contribute rather little to the total weight since the individual cell is 1000-fold lighter.
Typical genome sizes
Genome sizes vary enormously among species.
- \(3\times 10^{2}\)bp: viriods (two tweets)
- \(10^{4}\)bp: typical RNA viruses and phages (one page)
- \(10^{5}\)bp: animal DNA viruses (10 pages)
- \(10^{6}-10^{7}\)bp: bacterial genome (a serious book)
- \(3\times 10^{9}\)bp: human genome (one tength of all of English wikipedia)
Genome size among animals and plants correlates little with perceived complexity of the organism.
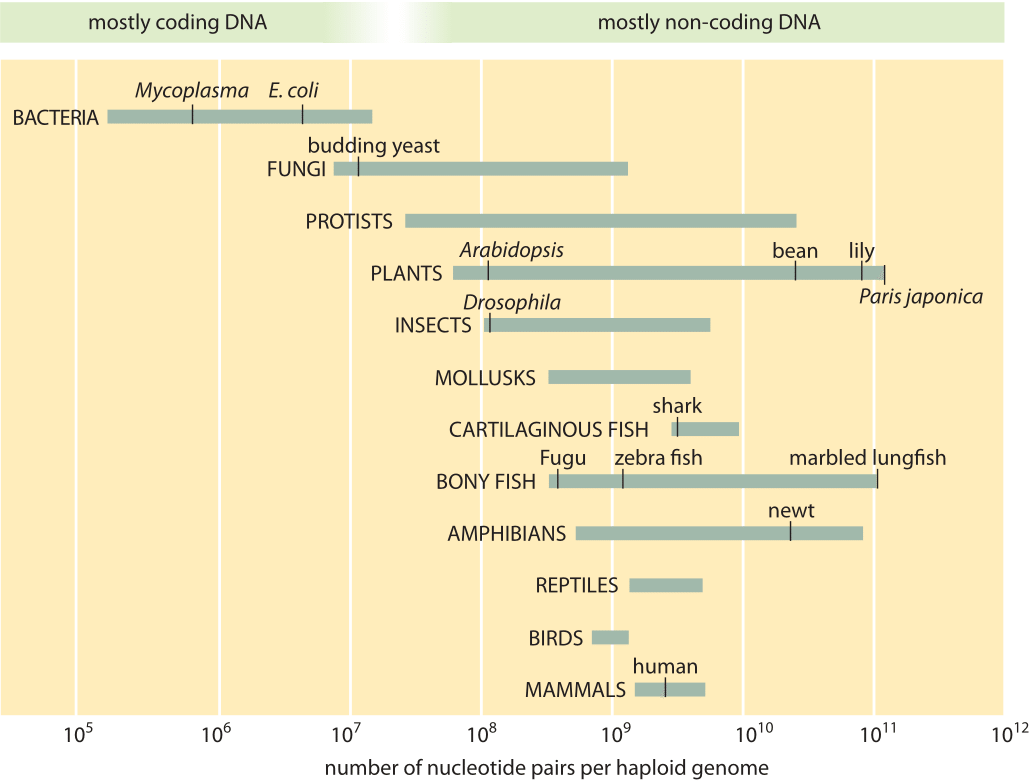Illustration of the range of genome sizes from bionumbers.org.
It is instructive to compare cell dimensions versus the length of the DNA molecule that needs to fit inside:
- \(10^{-6}\)m (1um): length of a phage genome.
- \(10^{-3}\)m (1mm): length of the bacterial genome (\(3\times 10^9\) bases a 0.3nm each)
- \(1\)m (1m): length of the human genome (\(3\times 10^9\) bases a 0.3nm each)
We see that DNA is much longer than the containing cells. An amusing litte calculation: if DNA from all \(10^{13}\) cells of a human body was strung together, it would cover the distance to the sun (\(1.5\times 10^{11}\)m) more than 100 fold (accounting for the diploid nature).
Concentrations and molecule counts
Concentrations are number of molecules per volume. There are typically measured as moles per liter, that is \(6\times 10^{23}\) molecules per \(10^{-3}m^{3}\). For our purposes, it is useful to express this as number of molecules per femtoliter or \(\mu m^3\): 1M=\(6\times 10^{23}/10^{15}\mu m^3 = 6\times 10^{8}/\mu m^3\) Hence one nM corresponds to roughly one molecule per bacterium, pM to one molecule per eukaryotic cell. The small volume of cells and nuclei there for means than many proteins are only present in small numbers. Hence their individual behavior and the associated stochasticity can be very important. When thinking about rare molecules, for example signaling molecules, numbers are a better guide than concentrations. If you have a binding partner with an affinities below these numbers, it will suck up every single molecule in the cell!
Illustration of the range of concentrations from bionumbers.org.
Forces and energies
So far, we have looked at dimensions and the objects involved could have been dead or alive. Lets now turn to the energies, power, and forces. From our daily live, we are used to power of about 100W. This would be your standard (old fashioned) light bulb or the typical power of the human body. Energy is stored in batteries, reservoirs, or petrol. In cells, the energy currencies are very different. The ultimate source of energy (free energy, really) is the sun. It emits black body radiation at a temperature of 5800K which corresponds to an emission maximum at a wavelength of 550nm in the visible range. A single photon with wavelength \( \lambda = 500nm\) has the following energy:
$$E = \frac{hc}{\lambda}\approx \frac{1.24 eV\mu m}{\lambda}\approx 2.5eV$$
Electron volt (eV) is a typical unit of energy used in physics corresponding to the energy required to move one election one Volt up in an electric potential. Chemists like to measure energy in \(kJ/mol\) or \(kcal/mol\), but in a biological system, different energy units are often more convenient. The most important energy scales in biological systems are the thermal energy kT and the energy released when hydrolyzing ATP to ADP. The scale kT is important since process that operate on the scale of kT or below happen spontaneously and reversibly. Hence it is always important consider an energy difference in relation to kT
$$kT \approx 0.025eV \approx 0.6 kcal/mol \approx 2.5 kJ/mol \approx 4pN \times nm$$
One visible photon is therefore about 80kT and it is plausible that individuals visible photons can drive biological processes. The dominent energy currency of the cell is ATP which is hydrolyzed to ADP
$$ATP + H_2O \rightarrow ADP + P_i \quad -30 kJ/mol \approx -12kT$$
Again, one ATP hydrolysis is above the thermal energy scale, but not all that far away. In practice, the amount of energy released in ATP hydrolysis can vary by a factor of two depending on Mg\({}^{2+}\) concentration and the concentrations of ATP and ADP.
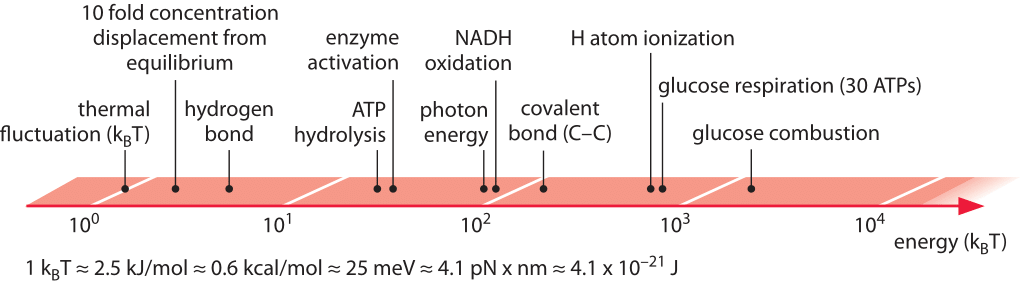A handy overview of energy scales from bionumbers.org.
Estimating stuff
Molecular motors
Cells have molecular motors that they use to move things around, drive cilia and flagella, or open up the DNA double strand. Most of these hydrolyze ATP, one molecule at a time. Some of these motors (kinesin and dynein) move in steps along filaments. These steps are on the order of 10nm. Assuming the energy of one ATP hydrolysis is converted with 100% efficiency into mechanical energy, we expect a maximum force (stall force) of
$$ \frac{12kT}{10nm} \approx \frac{48pN nM}{10nm} \approx 5pN $$
This estimate is surprisingly accurate -- most "walking" molecular motors have stall forces in this range. We will explore in the coming weeks what this implies for speed and maximal cargo size.
Genome replication
If a genome has a single origin of replication, the rate of genome replication \(\kappa\), genome size \(L\), and division time \(\tau\) are naively related by
$$ \kappa = \frac{L}{\tau} = \frac{5\times 10^{6}}{2500s} \approx 2\times 10^3/s $$
where we have used a typical bacterial genome size of 5Mb and a division time of 40min. 2000 bases per second is not far off, but probably a factor of 5 too high. Furthermore, E.coli can divide in 20min rather than 40min. The discrepancy can resolved by observing that (i) replication proceeds via two replication forks, and (ii) the next replication is started before the first one is complete.
Eukaryotic replication machinery is no faster than the prokaryotic ones, but the genomes are 1000 fold larger. To replicate their genomes in reasonable time eukaryotic genomes have 1000s of origins of replication.
The number of ribosomes
In an exponentially growing bacterial culture, biomass doubles once every division time. About one fourth of the cell mass is protein, which comes down to
$$ N_{aa} = 0.25 \times 10^{-12} g/cell \times 6\times 10^{23} \frac{Da}{g} / 100 \frac{aa}{Da} \approx 10^9 aa/cell $$
amino acids per cell that need to be synthesized every 20min and incorporated in to peptides. Peptide synthesis rate of 10aa/s, a single ribosome can process about \(10^4\) amino acids per cell cycle, suggesting the cell needs at about \(10^5\) ribosomes. This is roughly what is measured. Again, bionumbers.org has a very nice description of this problem. Importantly, this quick calculation tells us that ribosomes make up a substantial fraction of the total cell proteome (they certainly dominate the RNA pool).
Assignments
- collect 10 different entities (viruses, bacteria, spores, cell types) and calculate the fraction of the cell/organelle that is DNA
- How do you expect the ribosome fraction to vary with growth rate?