Analyzing a FRAP experiment
 Image by bioquant Heidelberg.
Image by bioquant Heidelberg.
Before we start with sophisticated calculations it is useful to develop some intuition for the problem
- we want to estimate \(D\) with units \(length^2/time\)
- somehow, a length scale and a time scale need to be involved
- the length scale available is the size of the bleached window \(w\)
- a plausible time scale would be the time to 50% recovery in the middle \(t_{1/2}\)
Hence we would expect that the diffusion coefficient is roughly \(D\sim w^2/4t_{1/2}\).
Solution of the diffusion equation in a bounded domain
Let's see how this simple reasoning compares to a more careful calculation.
Consider a box of length \(L\) with impermeable boundaries. The middle part between \(L/4\) and \(3L/4\) is bleached away. Evidently the Gaussian solution we considered last week does not fullfil the boundary conditions and the method of mirror solutions doesn't work with two boundaries. However, there is still a general solution to the problem which involves a number of useful generic concepts. We want to solve the diffusion equation without an advection term \(v=0\). $$\frac{\partial P(x,t)}{\partial t} = D\frac{\partial^2 P(x,t)}{\partial x^2}$$ such that \(\frac{\partial P(x,t)}{\partial x}\) vanishes at \(x=0,L\).
Let's try a factorized ansatz: \(P(x,t) = f(x)g(t)\). Substituting this into the diffusion equation, we find $$ f(x)\frac{\partial g(t)}{\partial t} = Dg(t)\frac{\partial^2 f(x)}{\partial x^2} $$ Dividing both sides by \(f(x)g(t)\), we find $$ \frac{1}{g(t)}\frac{\partial g(t)}{\partial t} = D\frac{1}{f(x)}\frac{\partial^2 f(x)}{\partial x^2} = -\lambda $$ where \(\lambda\) is a constant that does not depend on \(x\) or \(t\). (The RHS depends only on \(x\), the LHS only on \(t\), hence both sides need to be constant).
The solutions for \(g(t)\) and \(f(x)\) are $$ f(x) = a\cos(\sqrt{\lambda/D}x) + b \sin(\sqrt{\lambda/D}x) \quad \mathrm{and}\quad g(t) = ce^{-\lambda t} $$ The coefficients \(a,b,c\) and \(\lambda\) have to be determined from the initial and boundary conditions. Evidently, \(b=0\) since the \(\sin\) has non-zero slope at \(x=0\). Hence only \(\cos\) terms remain. To fulfill the boundary condition at \(x=L\), we require \(\sqrt{\lambda/D}L=n\pi\), where \(n=0,1,2,3,\ldots\). We therefore conclude that only a discrete set of \(\lambda\) values are admissable: $$ \lambda = \frac{Dn^2\pi^2}{L^2} $$ The elementary solution corresponding to a particular \(n\) is therefore $$ p_n(x,t) = e^{-\frac{Dn^2\pi^2}{L^2}t}\cos(n\pi x/L) $$
Since the diffusion equation is linear, any linear combinations of these elementary solutions is a solution: $$ P(x,t) = \sum_{n=0}^\infty a_n p_n(x,t) $$ This solution will respect the boundary conditions at all times. The coefficients \(a_n\) need to be chosen such that the initial conditions is full-filled (if this looks similar to a Fourier transform to you, you are exactly right!).
To this end, it useful to remember the orthonormality relations of trigonometric function. Specifically $$ \int_0^L \cos(n\pi x)\cos(m\pi x) = \frac{L}{2}\delta_{nm} $$ Multiplying the initial condition with \(\cos(n\pi x/L)\) and integrating yields $$ \int_0^L dx P(x,0)\cos(n\pi x/L) = \frac{La_n}{2} = \frac{L}{n\pi}\left(\sin(n\pi/4) - \sin(3n\pi/4)\right) $$
When including only the first couple of modes, we approximate the initial condition as follows:
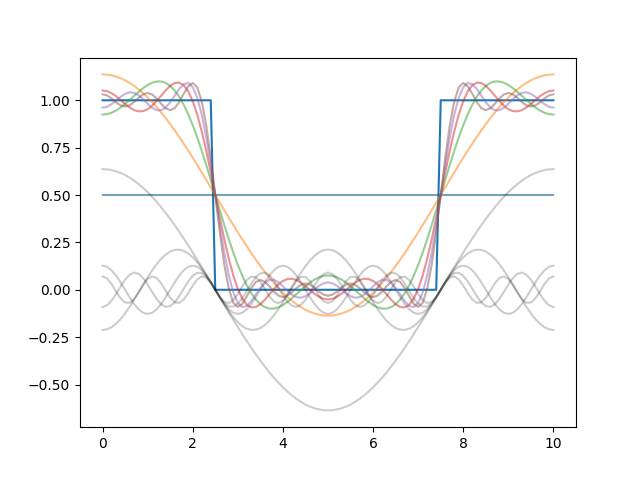
The modes corresponding to large \(n\) decay very fast, and the wiggliness of the solution goes away very quickly:
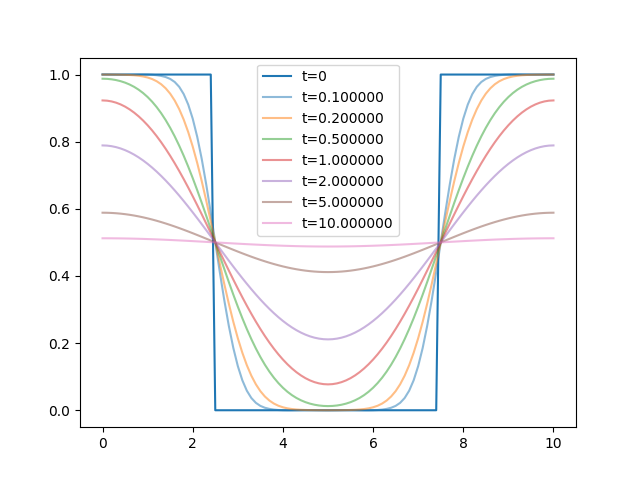
The script generating these figures is available here.
After a little while, the only remaining modes are the constant mode and the \(n=2\) mode, which predicts that the approach of the fluorescence profile to a uniform distribution is exponential $$ P(L/2,t) \sim 0.5 - a_2 e^{-4D\pi^2/L^2t} $$
Typical diffusion coefficients
- GFP in eukaryotic cells: \(\sim 25 \mu m^2/s\)
- GFP in prokaryotic cells: \(\sim 10 \mu m^2/s\)
- mRNA (actin in mouse): \(\sim 0.2 \mu m^2/s\)
- \(\mathrm{H_2O}\) molecule in \(\mathrm{H_2O}\): \(\sim 2000 \mu m^2/s\)
- \(\mathrm{H^+}\) molecule in \(\mathrm{H_2O}\): \(\sim 7000 \mu m^2/s\)
→ protein: \(\sim 10\mu m^2/s\), small molecule: \(\sim 1000 \mu m^2/s\), big polymer: \(\sim 0.2 \mu m^2/s\).
The Stokes-Einstein relation
Above we discussed how diffusion coefficients can be measured by FRAP. In fact, there is simple law that relates the diffusion constant to other properties of the medium and the diffusion particles: this law is called the Stokes-Einstein relation. Before we derive it, lets take a moment to think about which quantities might matter:
- big things diffuse more slowly, hence the radius \(r\) with units \(length\) is important
- diffusion is thermal motion, hence \(kT\) with units \(energy\) should be relevant
- diffusion is slower at high viscosity, hence \(\eta\) with units \(Force\cdot time/area\) will matter. (viscosity is the factor relating the force per unity area to the velocity gradient in fluid flow.)
How can we combine these quantities to give us a diffusion constant with units \(length^2/time\)? Clearly, \(\eta\) has to be in the denominator and \(kT\) in the numerator. Their ratio has the following units:
$$ \frac{kT}{\eta}\quad \mathrm{has\ units}\quad \frac{Force\cdot length\cdot area}{Force \cdot time} = \frac{length^3}{time}$$
Hence \(kT/\eta r\) has the right units and we expect the diffusion coefficient to scale as
$$D \sim \frac{kT}{\eta r}$$
Let's see how this holds up when analyzing the problem more carefully. Einstein considered diffusion in a general potential. We will assume here we have a harmonic potential \(U(x) = \alpha x^2/2\), i.e., a force \(F = \alpha x\) is pulling the particle back to \(x=0\). The motion of the particle is governed by the diffusion equation
$$\frac{\partial P(x,t)}{\partial t} = D \frac{\partial^2 P(x,t)}{\partial x^2} + \alpha \mu \frac{\partial P(x,t)}{\partial x}$$
where \(\mu\) is the mobility of the particle, i.e., the relationship between velocity and pulling force in viscous media. Mobility is the inverse of friction. At steady state, the distribution of the particle is
$$P(x) = \frac{1}{\sqrt{2\pi D/\alpha}}e^{ - \frac{\alpha x^2}{2D}} $$
However, the Maxwell-Boltzmann distribution requires that the equilibrium distribution is also proportional to \(e^{-\alpha x^2/2kT}\). Hence we find
$$ D = \mu kT $$
This is one example of a fluctuation-dissipation relation that connects macroscopic quantities such as mobility with the microscopic quantities such as the diffusion coefficients.
Next, we need to consider how the mobility is related to the geometry of the particle and the solution. This is given by Stokes' law that relates the friction force to the size of the sphere and the viscosity:
$$ \mu = \frac{1}{6\pi \eta r} $$
Deriving this is a standard exercise in fluid dynamics, but nothing that we will go into here. Have a look at the wikipedia page for Stokes' law if you are curious.
Putting the Einstein relation and Stokes' law together, we obtain the Stokes-Einstein relation
$$ D = \frac{kT}{6\pi \eta r} $$
The remarkable fact about this equation is that \(\eta\) can be measured at macroscopic scales and the microscopic structure does not feature explicitly. Nevertheless, together with the molecular radius and the energy scale \(kT\), it determines the diffusion coefficient of microscopic particles. Our intuitive scaling ansatz above was off by the factor \(6\pi\), but did capture the essence of the problem.
The viscosity of water at room temperature is
$$\eta_0 = 0.001\frac{N s}{m^2} = 10^{-15}\frac{N s}{\mu m^2} = 10^{-3}\frac{pN s}{\mu m^2} $$
The cytosol typically has a 3fold higher viscosity. So let's see how well the numbers given above compare to the prediction (Stokes' law assumes a perfect sphere, so we don't expect perfect agreement).
$$ D = \frac{kT}{6\pi \eta} \frac{1}{r} \approx \frac{4pN \cdot nm \cdot \mu m^2}{20\cdot 3\cdot 10^{-3} pN s}\frac{1}{r} = \frac{1}{r} \frac{\mu m^3}{15s} $$
For GFP with an radius of about 2nm, we find \(D\approx 33 \mu m^2/s\) -- a little high but not too bad. For a water molecule with \(r\approx 0.1 nm\), our predictions is \(D = 660\mu m^2/s\) in the cytosol and \(2000\mu m^2/s\) in pure water as expected.
Diffusion in different dimensions
So far all our calculations were done in one dimension while most examples we considered were in three dimensions. In fact, in biological systems diffusion is important in 1,2, and 3 dimensions.
- One dimensional problems: diffusion on DNA, along axons, along microtubules, actin filaments etc.
- Two dimensions: diffusion happens within membranes. Membranes are fluid and lipids or proteins move in two-dimensional sheets
- Three dimensions: cytosol, nucleus, signaling between cells.
Luckily, there are only a few differences when going from one to two to three dimensions. The random kicks a particle experiences from the surrounding molecules are independent in different directions and we can in principle look at each direction separately. The latter is the reason why looking only at one dimension has gotten us so for. Going through the same motions for multiple dimensions as previously for one dimension we arrive at a multi-dimensional diffusion equation
$$ \frac{\partial P(\mathbf{x},t)}{\partial t} = D_i \sum_i \frac{\partial^2 P(\mathbf{x},t)}{\partial x_i^2} - \sum_i \frac{\partial }{\partial x_i} v_i P(\mathbf{x},t) $$
For constant advection this has the solution
$$P(\mathbf{x},t) = \frac{1}{(4\pi D t)^{d/2}} e^{-\frac{\sum_i (x_i-v_i t)^2}{4Dt}} $$
Without advection (\(v_i=0\)), the typical distance traveled after time \(t\) is \(\Delta x = \sqrt{2dDt}\). This simply an example of the well known fact that variances add and standard deviations grow as square root.
One important difference, however, is the number of times a molecule returns to the vicinity of the origin at \(x_i=0\). In one dimension, this happens infinitely often, in two dimensions this happens but sometimes involves long waits, and in three dimensions this is not guaranteed to happen. (It is impossible to get lost in 1d, there is hope in 2d, and you rarely find home when lost and drunk in 3d).
How fast do things move?
The typical genetic energy of every particle is \(\frac{mv^2}{2}\approx \frac{kT}{2}\) (we are ignoring the factor of 3 for each spatial dimension). The velocity is therefore given by
$$ v = \sqrt{\frac{kT}{m}} \approx \sqrt{\frac{4 pN\cdot nm}{m}} = \sqrt{\frac{4 \cdot 10^{-21} N m}{m}} = \sqrt{\frac{4 \cdot10^{-21} kg}{m}}\frac{m}{s} $$
A protein of 30kDa weighs about \(5\times 10^{-23}\)kg suggesting a velocity of 10m/s. A water molecule with just 20Da (\(3\times 10^{-26}\)kg) would move at several 100m/s.
If we compare the speed to the diffusion constant, we can work out how often the particle changes direction. The mean free path (distance without substantial change of direction) is given by \(\delta x = \delta t v\). The number of steps in time \(t\) is \(n = t/\delta t\) and the total displacement is then
$$\Delta x = \sqrt{2Dt} \sim \sqrt{\delta x^2 n} = \sqrt{t \delta t v^2} $$
Hence the \(\delta t \sim D/v^2 \) which for water would evaluate to \( 2000 \mu m^2 s/10^{17} \mu m^2 = 2\times 10^{-14}s\). During this time, a water molecule travels about \(10^{-10}m\), that is about one atomic radius.