Many of the most important molecules in biology are polymers. They carry information (DNA, RNA), all proteins are polypeptides, and they provide structure and stability in form of the cytoskeleton. The microscopic properties of these different polymers depend on their molecular structure, but on larger scales their behavior is governed by a few mesoscopic parameters such as stiffness, charge, and self-interaction. We will discuss properties of
- single stranded RNA and DNA
- double stranded DNA
- actin filaments
- microtubules
and study general models of polymers. In addition to introducing properties of polymers, this lesson will also serve to revise concepts from the chapters on diffusion and random walks.

Micrograph of bacteria phage DNA adsorbed to a 2D surface (by R. Roberts, NEB).
The freely jointed chain model
In the above micrograph, it is obvious that DNA often changes direction in a seemingly random way. It might therefore by a good starting point to model polymer configurations as random walk of the type we have encountered when discussing diffusion. The simplest models of polymers approximate this polymer configuration by discretizing the molecule into short straight segments of length \(d\) followed by a complete randomization of the direction.
Consider a chain of \(N\) stiff segments of length \(d\). The end-to-end distance of that chain is then
$$\vec{R} = d\sum_i^N \vec{e}_i$$
where \(\vec{e}_i\) are unit vectors of random direction. The average squared end-to-end distance is therefore
$$\langle \vec{R}^2 \rangle = d^2\sum_{ij}^N \langle\vec{e}_i\vec{e}_j\rangle = d^2N$$
(products of vectors here are scalar products, that is \(\vec{v}\vec{u} = v_xu_x+v_yu_y+v_zu_y = |v||u|\cos(\phi_{uv}\) with \(\phi_{uv}\) being the angle between the vectors). The last identity hold since all off-diagonal terms \(\sum_{i\neq j}^N \langle\vec{e}_i\vec{e}_j\rangle\) average to zero since the average projection of one random vector onto any other vector vanishes. The diagonal term, however, contributes since \(\langle\vec{e}_i\vec{e}_i\rangle = 1\). Hence we recover the same \(\sqrt{N}\) scaling that we found for random walks.
By analogy, we know that the distribution of end-to-end distance will behave exactly like a diffusing particle that moves in a random direction at every step and the distribution of the end-to-end distance is given by
$$ P(\vec{R}) = \left(\frac{3}{2\pi N d^2}\right)^{3/2} e^{-\frac{3(R_x^2 + R_y^2 + R_z^2)}{2Nd^2}}$$
The additional factor of three accounts for the fact that the total average squared end-to-end distance is \(Nd^2\). Each spatial dimension contributes one third of that variance.
The picture below shows measurements of the mean squared distance of chromosomal markers in interphase chromatin in mammalian cells. The squared distance increases linearly with genomic separation, as expected from a random polymer walk.
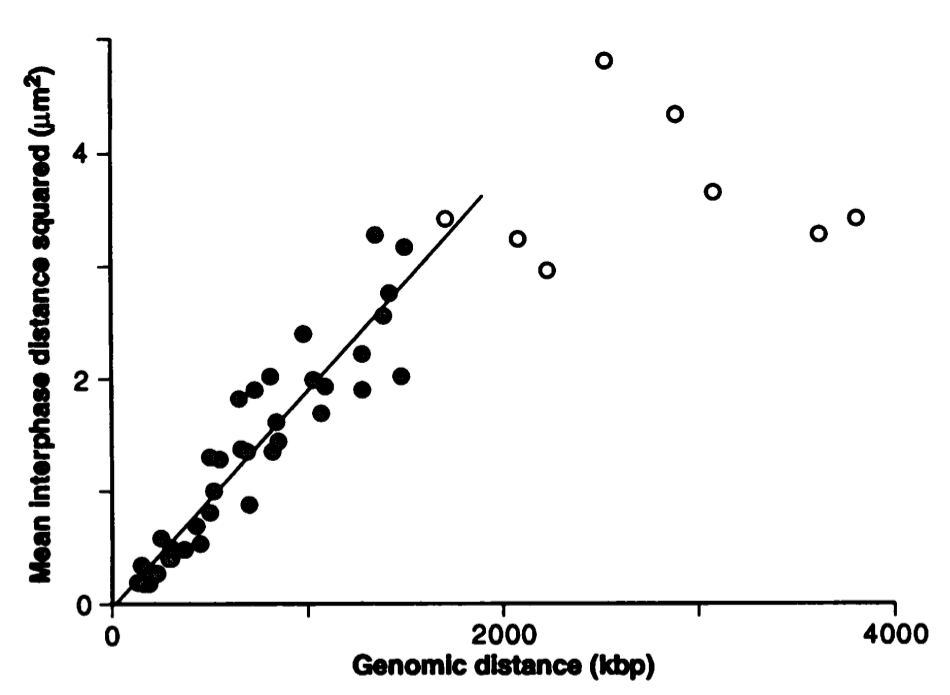
van den Engh et al, Science 1992
From the linear increase of squared distance, we can estimate the segment length \(d\) as follows:
$$\langle R^2(s) \rangle \approx 1.5\frac{\mu m^2}{Mbp} s = 1.5\frac{\mu m^2}{Mbp} N d = Nd^2 $$
Here \(d\) is measured in Mbp which corresponds to \(\approx 300\mu m\). One finds \(d = 1.5\frac{\mu m^2}{Mbp} = 5nm \). Hence the segment length of the chromatin fiber seems to be short and rougly comparable to the histone diameter (\(\sim 10nm\)).
Excurs: The central limit theorem and Gaussian distributions
The central limit theorem states that if you sum \(N\) random variables with variance \(\sigma^2\), the distribution of the sum will be Gaussian with variance \(N\sigma^2\). This is the reason why the end-to-end distance is Gaussian, and why the diffusion equation admits a Gaussian solution.
For concreteness, lets do derive the end-to-end distribution separately for the different cartesian coordinates, e.g. \(R_x = d\sum_j^N e_{jx}\). The probability for observing \(R_x\in [x, x+dx]\) is given by the product \(\rho(x)dx\) of the probability density \(\rho(x)\) and \(dx\). For each monomer, we average over all possible orientations which can come from any part of the \(4\pi\) sphere. The integral over this sphere is \(\int_0^{\pi}\frac{d\phi \sin \phi}{4\pi}\int_0^{2\pi} d\theta\) where \(\phi\) is the angle with the x-axis. The density for the x-coordinate of the end-to-end distance is then is given by
$$\rho(x) = \int_0^{\pi}\int_0^{2\pi} \prod_j\frac{d\phi_jd\theta_j}{4\pi}\sin(\phi_j) \delta(d\sum_i \cos(\phi_j) - x) = \int_0^{\pi}\prod_j\frac{d\phi_j}{2}\sin(\phi_j) \delta(d\sum_i \cos(\phi_j) - x) $$
To evaluate this expression, we apply a Fourier transform
$$\hat\rho(\omega) = \frac{1}{2\pi} \int dx e^{-i\omega x}\rho(x) \rho = \int_0^{\pi} \prod_j \frac{d\phi_j}{2}\sin(\phi_j) \int \frac{dx}{2\pi} e^{-i\omega x} \delta(d\sum_j\cos(\phi_j) - x)= \frac{1}{2\pi} \int_0^{\pi} \prod_j \frac{d\cos(\phi_j)}{2}e^{-i\omega d\sum_j\cos(\phi_j)}$$
which decouples the different integrals. The last term in the equations follows from the fact that the Fourier transform of the \(\delta\) function is identically one. In other words, you get a very sharp peak by overlaying many oscillating function that all agree in exactly one point, but cancel everywhere else. We can now separately evaluate the different integrals. Instead of evaluating them exactly, we assume (and later justify) that the relevant \(\omega\) is small and we can Taylor expand the exponential:
$$\int_{-1}^{1} \frac{dy}{2} e^{-i\omega d y} = \frac{e^{-i\omega d} - e^{i\omega d}}{2i\omega} \approx = \frac{-2i\omega d - i\omega^3d^3/3}{2i\omega} = 1 - \frac{\omega^2 d^2}{6} $$
We can ignore higher order terms, since they correspond to distances shorter than the individual step-size \(d\). Combining all terms yields
$$\hat\rho(\omega) = \frac{1}{2\pi} \prod_j (1 - \frac{d^2\omega^2}{6}) \approx \frac{1}{2\pi} e^{-\frac{N d^2\omega^2}{6}}$$
To solve for \(\rho(x)\), we have to invert the Fourier transform.
$$\rho(x) = \frac{1}{2\pi} \int d\omega e^{i\omega x -\frac{3N d^2\omega^2}{2}} = \frac{1}{\sqrt{2\pi Nd^2}}e^{-\frac{3x^2}{2Nd^2}}$$
The last integral can be reduced to a standard Gaussian integral by completing the square and the result is a Gaussian with variance \(Nd^2\). Lastly, we should check whether our assumption that \(\omega d\) is small is justified. Looking that the Gaussian inverse, we see that \(\omega\) values that contribute substantially to the solutiona \(\omega d < 1/\sqrt{N}\). Hence ignoring higher order terms was ok.
Worm-like chain model
The above model of freely jointed stiff segments is obviously an extreme simplification, albeit not totally unreasonable for single stranded RNA/DNA that change direction on the same length scale as the length of the monomers. dsDNA is stiff over many helical turns and a better model is one where the polymer is continuously changing direction due to infinitesimal bending. This bending requires energy and spontaneously occurs due to thermal activation. At absolute zero, the polymer would be in its lowest energy configuration, that is completely straight.
We can parameterize a polymer by the location \(\vec{r}(s)\) of the monomers in 3D as we move along the backbone \(s\). The tangent vector, that is the direction of the polymer, is given by the derivative \(\vec{t} = \frac{d \vec{r}(s)}{ds}\). Curvature correspond to change in direction, i.e., bending. The total bending energy is therefore given by
$$E_{bend} = \frac{\kappa}{2}\int_0^L ds \left(\frac{d^2 \vec{r}(s)}{ds^2}\right)^2 $$
By termal activation, the chain changes direction and it can be shown that the correlation in direction decays exponentially
$$\langle \vec{t}(0)\vec{t}(s)\rangle = e^{-s/l_p} $$
where \(l_p\) is known as the persistence length. It is related to the stiffness via $$l_p = \kappa/kT.$$ With this exponential form of the decorrelation, we can calculate properties such as the average squared end-to-end distance
$$ \langle r(L)^2 \rangle = \langle \int_0^L ds \vec{t}(s) \int_0^L ds' \vec{t}(s')\rangle = \int_0^L dsds' e^{-|s-s'|/l_p} = \int_0^L ds \left[\int_0^{L-s} dx e^{-x/l_p} + \int_0^{s} dx e^{-x/l_p}\right]$$ $$ \langle r(L)^2 \rangle = l_p \int_0^L ds[1 - e^{-(L-s)/l_p} + 1 - e^{-s/l_p}] = 2l_p \left[L - l_p (1 - e^{-L/l_p})\right] $$
Hence for long polymers, the typical squared end-to-end distance scales as \(l_p L = l_p^2 N\) consistent with the freely jointed chain above. For short polymers, we have \(\langle r(L)^2 \rangle = L^2(1-L/3l_p)\). In other words the polymer is mostly straight.
Measuring the force extension curves of biological polymers
This year's nobel prize in physics was partly awarded to Arthur Ashkin for the development of optical tweezers. Focussed laser beams trap tiny particles in the center of the focus where the light intensity is highest. Forces applied to these particle move the trapped particles slightly out of the focus of the beam and diffract light in a way that allows to measure the force applied.
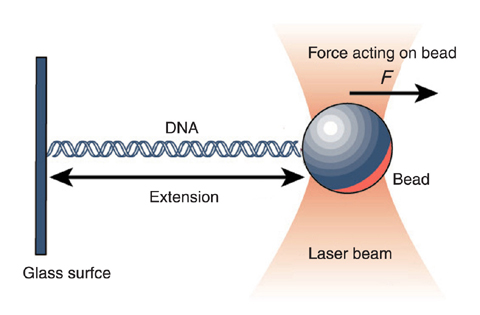
from umdberg.pbworks.com
Size of DNA coils of typical genomes
The persistence length of DNA at physiological conditions is about 50nm, that is about 150bp. The DNA of a bacterium is therefore 30000 persistance length long and the radius of gyration is on the order of \(200\times 50nm = 10\mu m\), i.e. about 10 times larger than the size of the cell. The problem is more severe for mammals or plants with their large genomes. Unconstrained, they genomes would occupy a ball of hundreds of \(\mu m\) in diameter.

Lysed E. coli. The remains of the bacterium is the blob in the middle.
Microtubules
Microtubules are very stiff polymers that are part of the cytoskeleton. They are the substrates on which dynein and kinesin motors run. There large diameter makes microtubules exceptionally stiff with a persistence length of the order of one millimeter. Hence microtubules are stiff on length scales much longer than the cell.
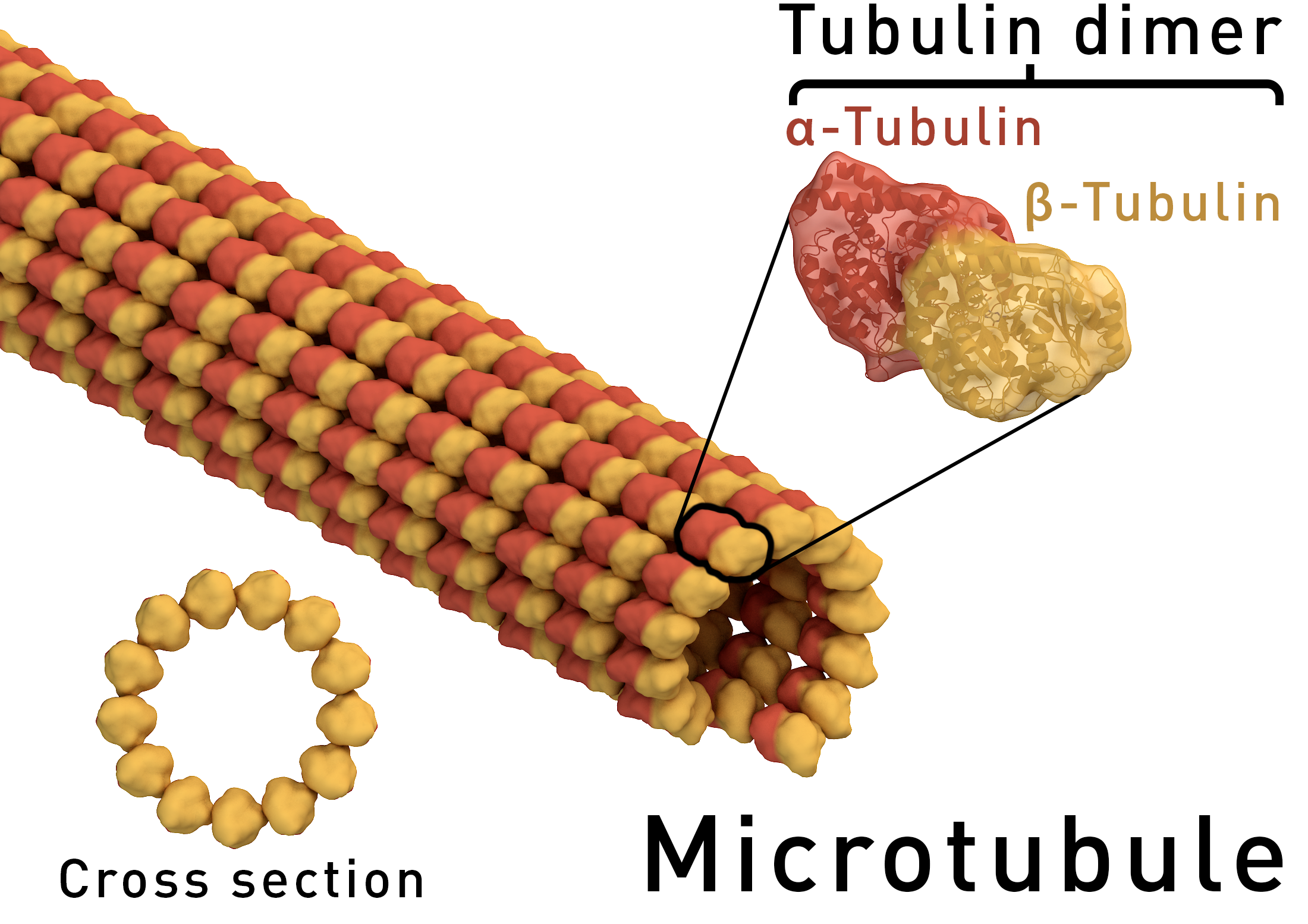
By Thomas Splettstoesser (www.scistyle.com) - Own work (rendered with Maxon Cinema 4D), CC BY-SA 4.0, Link
How does stiffness scale with diameter?
For sake of argument, assume the microtubule has a square crossection with edge length \(r\). When bending with a curvature radius \(R\), the outer part get longer by \(r/R\), while the inner part shrinks by that amount. At the same time, the width increases with \(r\), resulting a quadratic increase of the bending force with \(r\).