Early bright field microscopy revealed intricate intracellular substructures. The larger structures, such as the nucleus, golgi, ER, mitochondria etc are enclosed by lipid membranes that clearly separate inside and outside. Transport between compartments is controlled by pores and channels. Many other organelles, however, are not surrounded by a lipid membrane yet still are well defined and stable. Here, we will explore how these structures are formed and under what conditions they arise.
Slides with pictures and videos
Entropy and energy of multi-component solutions
The phase separation, or de-mixing, is driven by conflicting entropy and energetic (enthalpic) tendencies. A mixture prone to phase separation is characterized by energetically favorable interactions with the same type and less favorable interactions between types. Depending on temperature, concentration, salt condition etc the preferred state is either a mixed one or phase separated state.
Brangwynne et al, Nature Physics, 2015
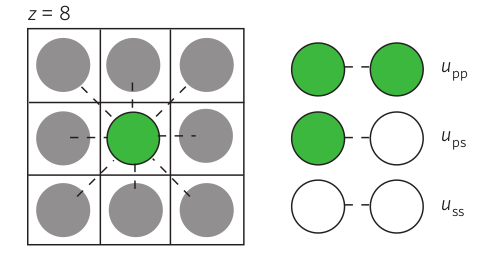
In the above picture, the white balls represent the solvent, the green balls the protein or polymer whose condensation we are interested in (we'll call it protein for simplicity). The interaction energy can be written as the number of contacts between solvent molecules \(u_{ss}\), between solvent and protein \(u_{sp}\), and between proteins \(u_{pp}\). The typical number of contacts one solvent molecule makes is called the coordination number \(z\). For simplicity, lets assume that monomers have similar size as solvent molecules and arrange them on a lattice. If the state of the systems is a random mix with monomer fraction \(\phi\), the energy of the system is
$$H = \frac{N z}{2} \left[(1-\phi)^2 u_{ss} + \phi^2 u_{pp} + 2\phi(1-\phi)u_{sp}\right]= \frac{N z}{2}\left[\phi(1-\phi)(2u_{sp} - u_{pp}-u_{ss}) + \phi(u_{pp}-u_{ss}) + u_{ss}\right] $$
The term proportional to \(\phi(1-\phi)\) is the contribution of contacts between the types, while the term proportional to \(\phi\) is simple the difference between the pure types. The take home here is that as a function of concentration \(\phi\), the enthalpy is a parabola that can either have positive curvature favoring mixtures or negative curvature favoring demixing.
Demixing is opposed by entropy: many energetically unfavorable states can have more weight than few favorable states. Entropy is the logarithm of the number states available given the constraints. Consider a lattice model of the solution and ignore for a moment that the monomors of the polymer are strung together.
Brangwynne et al, Nature Physics, 2015
In a random mixture, we can pick for each lattice site independently whether its solvent or monomer. This results in
$$ e^{S+c} = \frac{N!}{(N\phi)!(N(1-\phi))!} $$
configurations. The logarithm of this number is the entropy (up to an additive constant). To calculate its magnitude, we use the well known Stirling's approximation for factorials \(\log n! \approx n\log n - n\) and find
$$ S + c = N\left[\log N - \phi\log(\phi N) - (1-\phi)\log((1-\phi)N)\right] = -N(\phi\log(\phi) + (1-\phi)\log(1-\phi))$$
Combining the interaction energy with the mixing entropy, we arrive at the free energy of the idealized system:
$$ \frac{F}{N} = kT(\phi\log(\phi) + (1-\phi)\log(1-\phi)) + \phi(1-\phi) \frac{z(2u_{sp} - u_{pp}-u_{ss})}{2} $$
Whether the solution will spontaneously separate into a phase of high and low concentration of the protein, depends on whether the free energy of the homogeneous mixed system is lower than the sum of the energies of two systems at high/low monomer concentration.
Instability of a mixture
Consider a homogenous mixture with monomer concentration \(\phi\) and compare this to a two phase mixture in which one phase (fraction \(\alpha\)) has concentration \(\phi_1\) and the other phase (fraction \(1-\alpha\)) has concentation \(\phi_2\). To conserve mass \(\alpha \phi_1 + (1-\alpha)\phi_2 = \phi\). Under what conditions will a mixture of two phases will have lower energy than the homogeneous case?
The stability of a configuration depends on the curvature of the free energy in \(phi\). This is illustrated in the figure below.
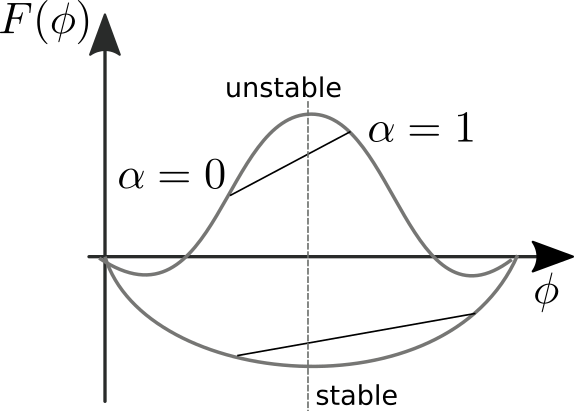
The free energy of a mixture with fraction \(\alpha\) lies on a straight line connecting the two pure phases with concentrations \(\phi_{1/2}\). Conservation of mass requires that the average concentration doesn't change, hence the relevant comparisons are all on a vertical line. This considerations immediately tells us that a mixture is stable if the free energy is convex, i.e., the curvature is positive. Otherwise, it is always possible to lower the free energy by splitting the solution into a mix of two phases.
Surface tension
Phase separation happens when like interactions are sufficiently strong to overcome entropy favoring mixing. At the surfaces of two phases, however, molecules enjoy a smaller number of like interactions than in the bulk of the either phase. Hence surfaces between phases are associated with a free energy cost. This cost results in a tendency to minimize the surface area given the volume and the optimal geometry is obviously a sphere. Effectively, the surface is under tension driving shapes towards the lowest free energy geometry. Surface tension has units energy/area or Newton/length.
When three different phases (or a solid, a liquid and a gas) meet, the three phase interface depends on the relative surface tensions associated with the three interfaces. The resulting behavior and contact angles can be calculated from the balance of forces at the contact line.
Nucleation
The relative contributions of free energy of the bulk and surface depend on the size of the droplet. For a spherical droplet, the free energy will scale with the radius as
$$ G(r) = -\alpha r^3 + \beta r^2 $$
where \(\alpha,\beta\) are positive constant with the appropriate dimensions. At very small \(r\), the free energy increases with \(r\) and small droplets are unstable. Only above the nucleation radius \(r^* = \frac{2\beta}{3\alpha}\) do droplets grow deterministically. This phenomenon is known as nucleation.