The cytoskeleton is an umbrella term for structural components of cellular organization. For a detailed overview of the cytoskeleton, you'll have to look at cell biology books like Albert's. Here, we will only have a cursory look at the basic properties of cytoskeletal filaments. The most prominent member of the cytoskeleton are
- microtubuli: stiff 25nm "rods"
- intermediate filaments: coiled-coils
- actin filaments: more flexible 8nm fibers, often branched
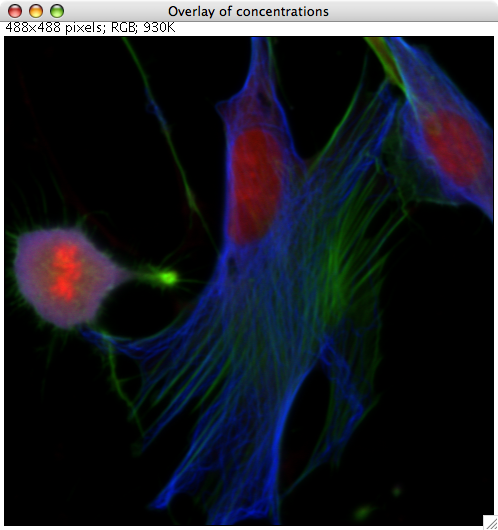
In this false-color image, microtubules are show in blue and actin in green (the DAPI DNA stain is red).
Microtubuli
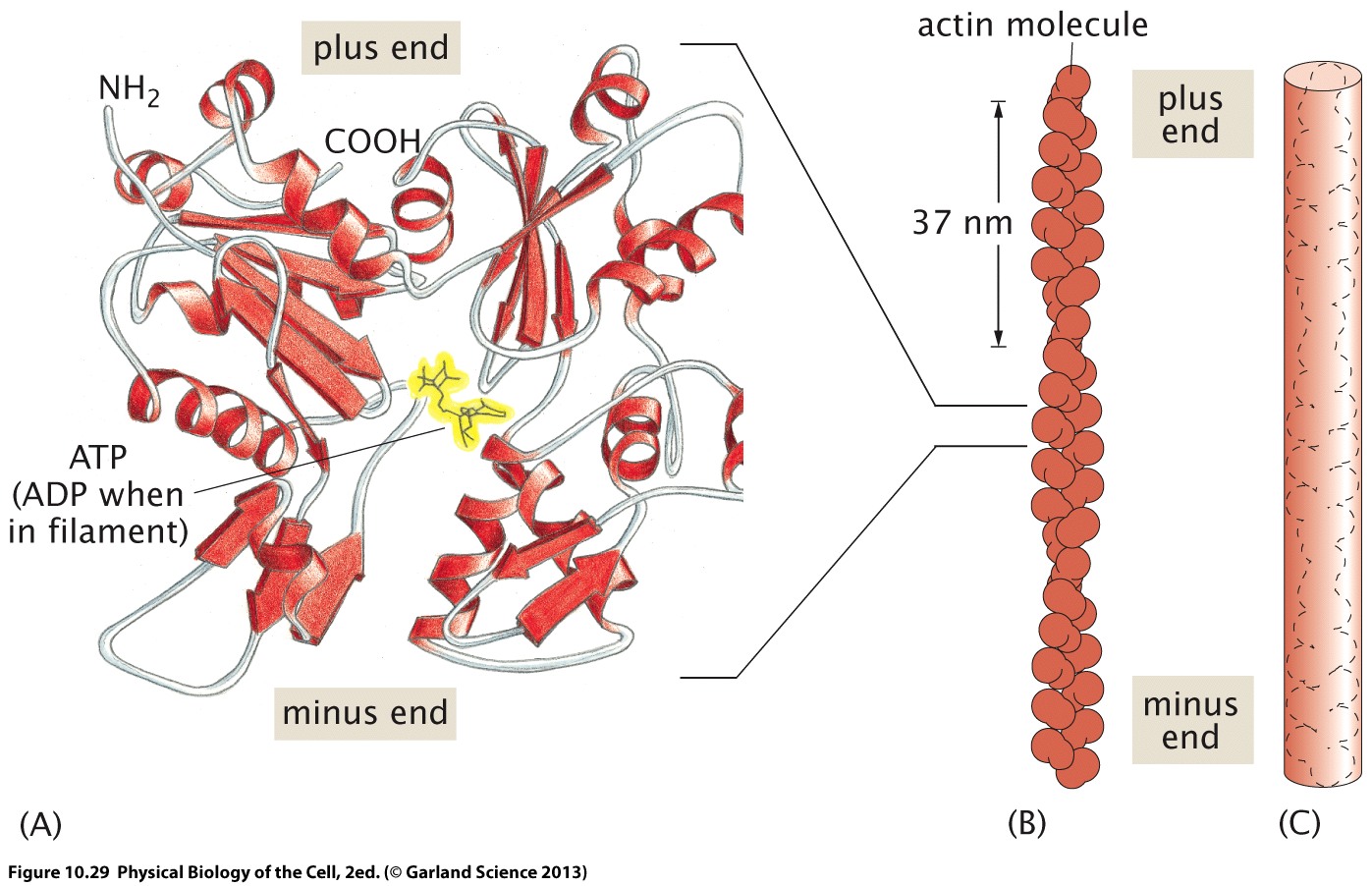
Microtubuli are made from hetero-dimers of alpha and beta tubulin. They assemble into a walled tube with a circumference of 13 hetero-dimers and a diameter of about 25nm. They are polar. One end is known as plus end, the other is the minus end.
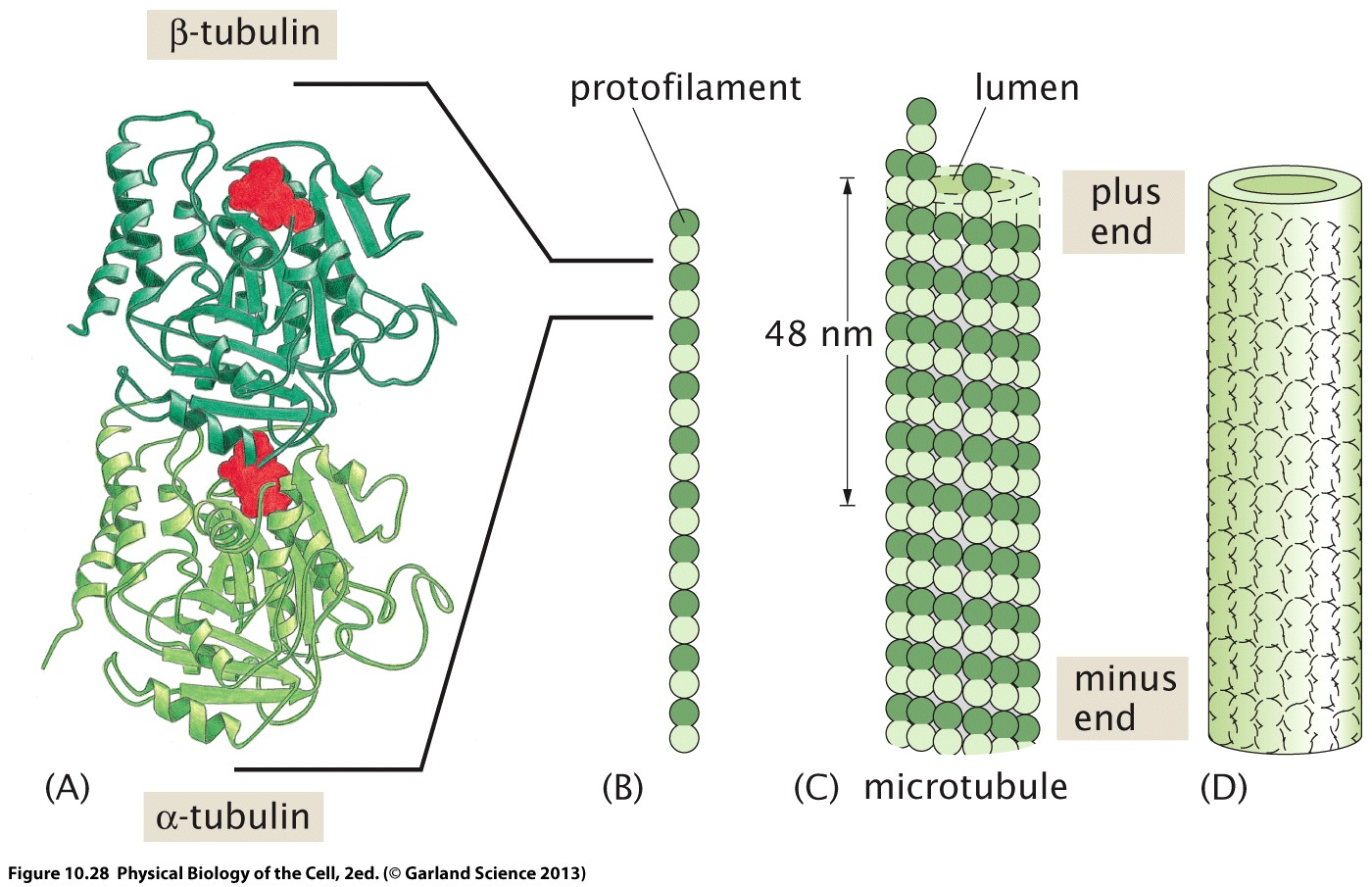
GTP molecules (shown in red) are trapped between the monomers. One of them is hydrolyzed upon polymerisation.
Microtubuli orchestrate the separation of sister chromatids during cell division. For that purpose, several microtubuli are assembled into bundles that start at the spindle and connect to the kinetochores on the replicated sister chromatids. Microtubuli also serve as "cargo lanes" kinesin and dynein molecular motors. Kinesin motors move towards the plus end, while dynein motors run the other way.
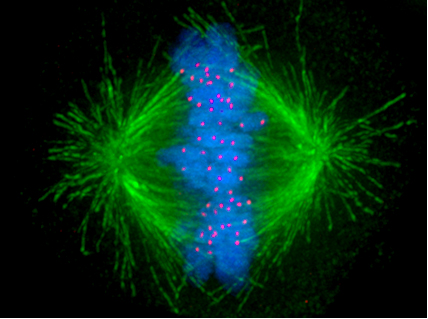
Pakorn Kanchanawon and Clare Waterman; Afunguy. source: wikipedia.org
Microtubules don't assemble spontaneously (the individual proto-filaments are unstable) but require microtubule organizing centers (MTOCs) to nucleate. Apparently many different structures can serve as MTOCs and initiate the polymerization of microtubules.
Actin
Actin filaments are composed to G-actin monomers and two protofilaments are wrapped around each other.
Myosin motors operate on and between actin fibers. There are many different types of myosins that carry cargo along fibers of slide actin fibers along each other.
Actin filaments often form branches and interconnected networks through actin binding proteins that crosslink various fibers. The actin cytoskeleton is central to cell motility and muscle contractility. The myson/actin network orchestrates many morphological changes during development.
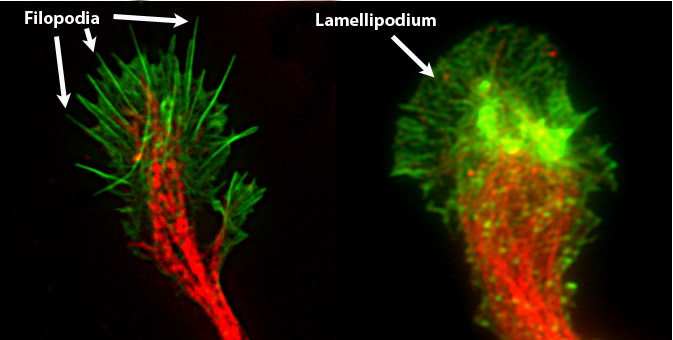
Growth cones are pushed forward by the myson/actin network, resulting in structures called filopodia and lamellipodia, see figure below. We will explore in greater detail how actin cytoskeleton can exert force and push cells and membranes forward.
by Chris1387. source wikipedia.org
Intermediate filaments
The term intermediate filament refers to a diverse group of coiled-coil proteins that are involved in variety of structural components of the cell, e.g. the nuclear lamina.
They are called intermediate because they have a ~10nm diameter, hence thicker than actin and thinner than microtubuli.
The precise function and assembly of intermediate filaments is much less understood than actin or microtubuli.
None of the proteins associated with these filaments seem to have motor activity.
They are extremely stable and extensible.
They are often described as supporting membranes, for example the nuclear membrane or the cell membrane, and maintain membrane integrity by distributing tensile forces.
wikipedia.org
The cytoskeleton is dynamic
Our experiences with the macroscopic world leads us to think that structural elements are static. Quite the opposite is true for cytoskeletal filaments. Actin and microtubuli in particular are constantly polymerizing and depolymerizing and some pathogenic bacteria have found ways to hijack the eukaryotic actin cytoskeleton. The graph below shows labeled actin and phase contrast images of listeria.

Listeria are an important human pathogen with a high case fatality rate (20%) that is typically transmitted via contaminated food. It can grow at low temperatures (in your fridge). Listeria infections are particularly problematic during pregnancy where they can cause meningitis of the fetus.
The bacteria invade host cells and induce polymerization of actin at one pole to move around in cells. The build-up of an actin network results in propulsion. Listeria move at about 0.2um/s, similar to the speed of migration of motile animal cells such as keratocytes. This given an actin monomer size of 3nm, this corresponds to AT LEAST 70 monomer incorporations per second. How the polymerization of actin generates forces was studied in detail by Mogilner and Oster.
The basic component of the model put forward by Moligner and Oster is that actin polymers bend through thermal fluctuations. Once they are bent and there is a gap between the bacterium and the actin fiber, further polymerization can occur. This results in a permanently bent polymer that pushes against the surface. In a slight twist, the bacterium also serves as a nucleus for new filaments and these filaments pull the bacterium back rather than push it forward. Only after they detach, they can polymerize further and push the bacterium forward. The balance of forces on the bacterium can be broken down into three components $$ F_{load} + f_a a = f_w w$$ where \(F_{load}\) is the viscous drag on the moving bacterium, \(f_a n\) is the product of the pulling force and the number of attached filaments, and \(f_w w\) is the pushing force and the number of pushing (working) filaments. The number of attached and working filaments is modeled as first order ODEs $$ \frac{da}{dt} = n - a \delta \quad \Rightarrow \quad \bar{a} = n/\delta$$ $$ \frac{dw}{dt} = a \delta - \kappa w \quad \Rightarrow \quad \bar{w} = n/\kappa$$ where \(\delta\) and \(\kappa\) are the detachment and capping (preventing further polymerization) rates.
The fact that the bacterium is both pulled and pushed complicates the analysis. The faster the bacterium moves, the higher is the pulling force, which in turn slows it down. In addition, the detachment rates will increase with the pulling force. Do find a consistent solution in this case, we need to specify how the forces and rates depend on the load and the velocity. To this end, we express the velocity as the $$ V = V_{max}e^{-f_wl/kT} - V_{dep} $$ as the difference between the polymerization and depolymerization velocity. The polymerization velocity is reduced by the force exerted by the bacterium by the exponential factor \(e^{-f_wl/kT}\) where \(l\) is the length of the monomer. This is a consequence of the equipartition theorem -- the probability of a gap opening of length \(l\) is Boltzmann in the work needed to do so. The dissociation rate, in contrast, is accelerated by the pulling force and the typical force applied to an attached actin filament is determined by the stiffness of the actin network, the speed of the bacterium, and the characteristic length of the attachment potential.
MORE TO COME -- SEE NOTES FOR THE TIME BEING
Buckling instability
Microtubules are the only cytoskeletal structure that resist compressive force. Others are good at tensile forces. But how much compressive force can a microtubule withstand? We discussed earlier that the persistence length of microtubules is about 1mm. Recalling that the persistence length is stiffness over kT, the stiffness is $$ \kappa = kT l_p = 4pN \mu m^2$$ Let's write down the energy of a microtubule of length \(L\) when a force \(F\) is applied. Then the microtubule bends, its end-to-end distance gets shorter. The curvature is commonly described by the radius \(R\) of the circle that overlaps with the microtubule's contour. The angle \(\theta = L/R\) and the end-to-end distance is $$ l = 2R\sin(L/2R) \approx L - \frac{L^3}{24R^2} $$ The total energy is then $$ E_{tot} = E_{bend} + E_{load} = \frac{\kappa L}{2R^2} - FL(1 - \frac{L^2}{24R^2}) = \frac{1}{L} \left[\frac{\kappa}{2}\theta^2 - FL^2(1 - \theta^2/24)\right] $$ As long as \(\frac{dE_{tot}}{d\theta}>0\), the beam is stable. But as soon as the force exceeds $$ F_c = \frac{12\kappa}{L^2} $$ the beam will buckle. This is known as Euler's buckling instability. As is intuitively clear, buckling becomes easier when the beam is longer -- one reason for frequent crosslinking.
NOTE: we have made an approximation here since the shape of the bent microtubule is not actually a part of a circle, but a sine. This changes the prefactor (replacing the 12 with \(\pi^2\)).
Assignments
- What is the diffusion limit on the actin polymerization rate? Assume an actin concentration of 0.3mM.
- What is the viscous drag on the bacterium? Assume a sphere of a diameter of one \(\mu m\) and a speed of 200nm/s.
- Look at Moligner and Oster, find the values for the dimensionless parameters, and plot the LHS and RHS of the result (their Fig 2, Eq. 12). Vary the parameters by +/- 50% and observe how the solution changes. Note that this will require numerical integration of the expression for \(\omega(v)\).
Solutions
Further reading
- Lectures on cell motility and the cytoskeleton by Julie Theriot
- Moligner and Oster, Biophys. J, 2003