Jacobus van't Hoff and Svante Arrhenius, two chemists in the late 19th century, described how equilibrium constants and reaction rates depend on temperature. Consider an reaction
$$ A+B\leftrightarrow C$$
with an equilibrium constant \(K\). In general, this equilibrium constant is temperature dependent and van't Hoffs equation states that
$$ \frac{d\log K}{dT} = \frac{\Delta H}{kT^2} $$
where \(\Delta H\) is the enthalpy change (that is the internal energy + \(pV\) if any expansion happens during the reaction). This equation can obviously be integrated between two temperatures (assuming that \(\Delta H\) is temperature independent). More usefully, the equation suggests an obvious way to plot and \(K\) and measure \(\Delta H\). Graphing \(\log K\) vs \(1/T\) should result in a straight line. The slope of this line the enthalpy of the reaction. The intercept \(1/T=0\) (that is infinite temperature) is the entropy change involved in the reaction. The latter holds because the equilibrium constant is related to the Gibbs free energy by \(K = e^{-\Delta G/kT}\) and
$$\Delta G = \Delta H - T\Delta S$$
Hence at infinite temperature, only the entropic part remains.
Arrhenius extended this reasoning to reaction rates, i.e., the rates that take A and B to C and vice versa. Clearly, the equilibrium constant is the ratio of the reaction rates and some degree of exponential dependence on temperature of the equilibrium constant will carry over to the rates. In general, however, the enthalpy can take any part along the reaction coordinate. This is typically assumed to be just a single peak.
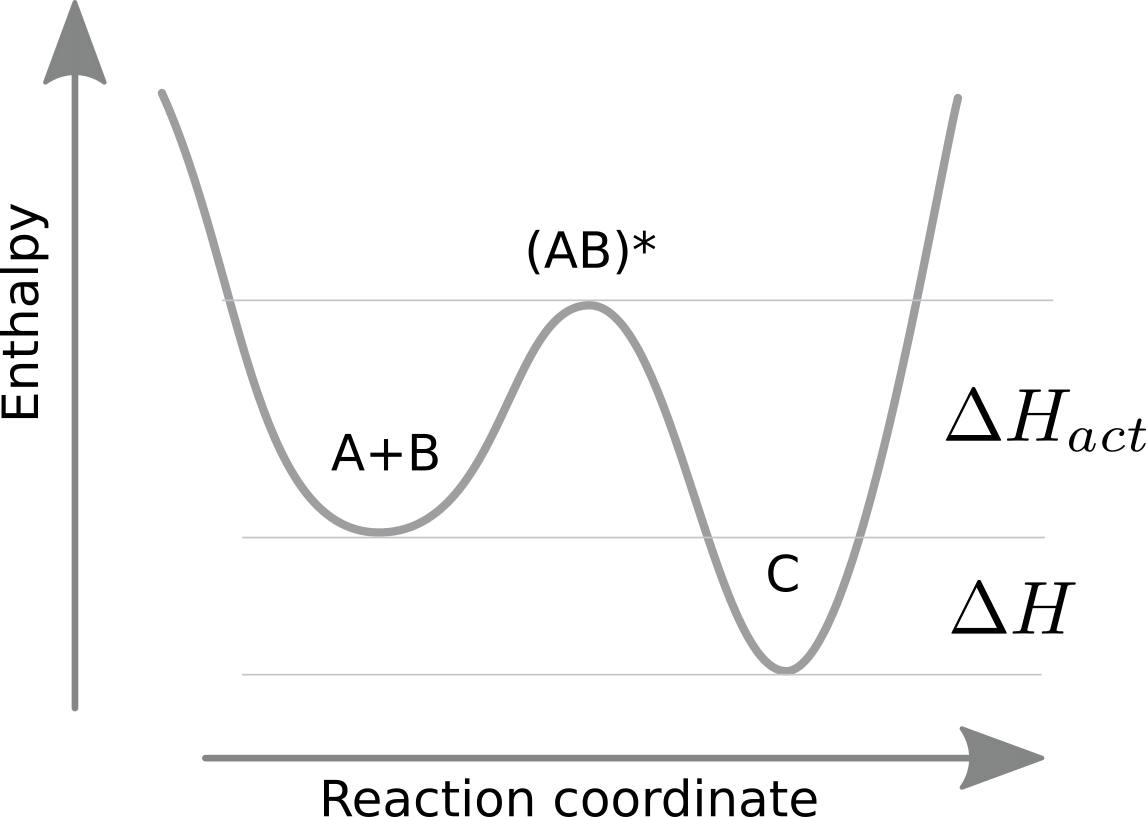
Arrhenius proposed that rates are exponential in the (negative) height of the energy barrier:
$$k^+ = \alpha e^{-\Delta H_{act}/kT} \quad \mathrm{and} \quad k^{-} = \alpha e^{-(\Delta H_{act} + \Delta H)/kT} $$
This behavior is explicit in so called Arrhenius plots that graph (in analogy to the discussion above) the logarithm of a rate against inverse temperature.
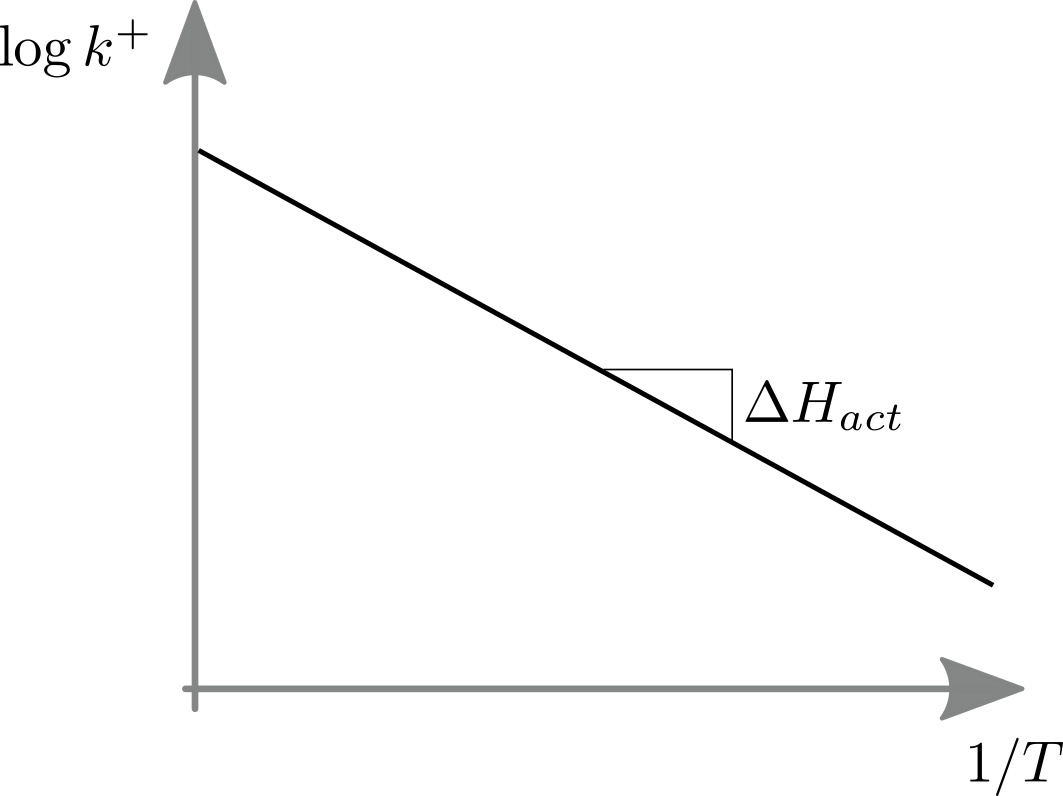
The slope of the log rate vs inverse temperature equals the activation energy.
The exponential dependence of a rate on an energy barrier has featured a number of times during the course with hand-waving explanation. One the other hand, we have calculate now rapidly reactants come together by diffusion and it seems natural to assume that the diffusion limited rate will play the role of the prefactor. The diffusion limited rate is then reduced by the energy barrier that needs to be overcome in addition to being in close proximity. We now want to look at this problem in a more formal, quantitative way.
One dimensional first passage problem
The first passage time is the time it takes for a system to first reach a certain state. We will exclusively look at systems with diffusive dynamics (inertia is rarely important within cells). In this case, the first passage can be modeled as a diffusion problem with an absorbing boundary at the target state.
The graph below illustrates our set-up.
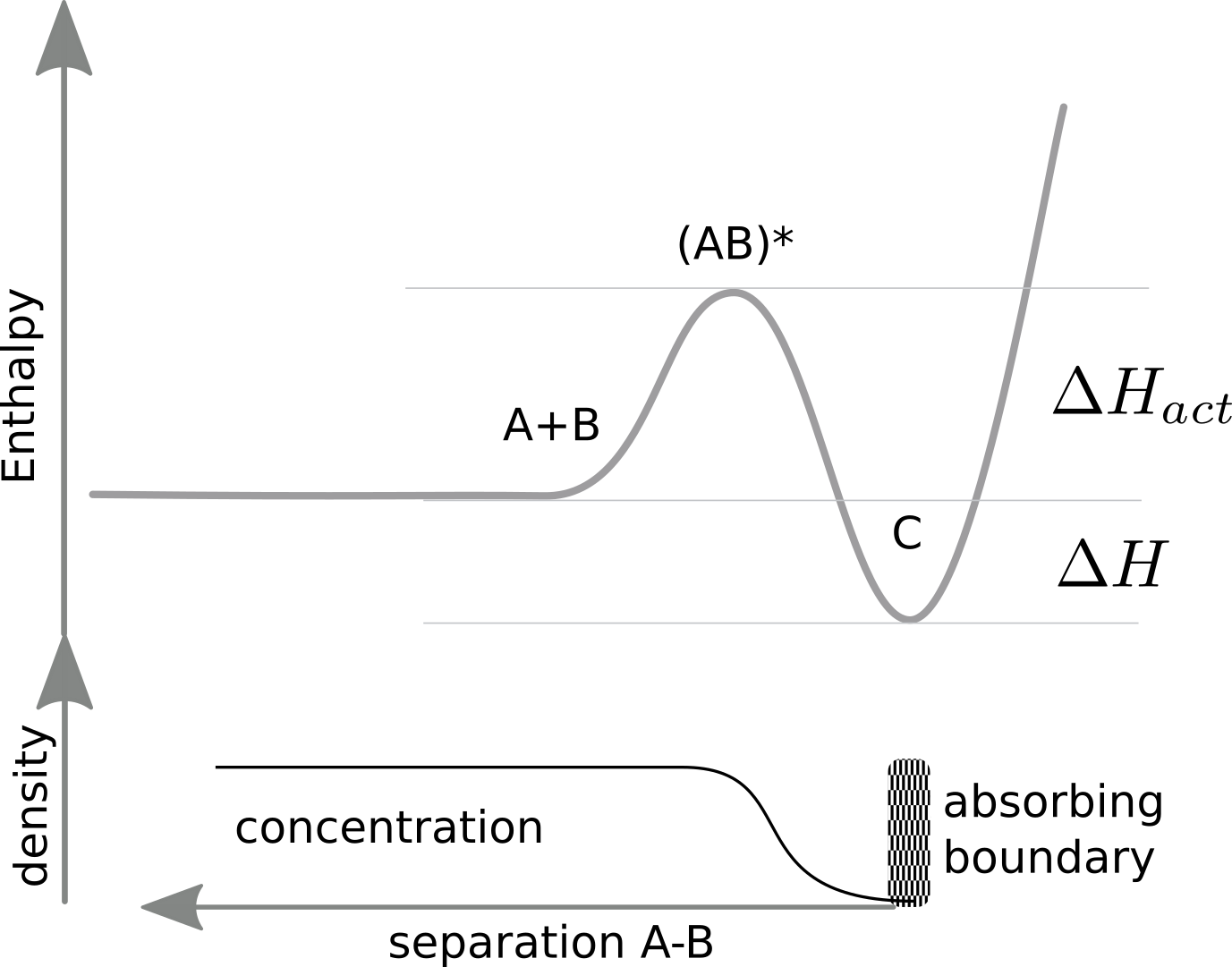
At long distances, the density of an A,B pair is simply the product of their concentrations. At short distance, the density is reduced by the energy barrier to overcome, that is the two species repel each other. The diffusion equation governing the density is
$$ \frac{dP(x,t)}{dt} = \mu kT\frac{d^2P(x,t)}{dx^2} + \mu\frac{d E}{dx} \frac{dP}{dx}$$
Here, we are using the Einstein relation that the diffusion constant \(D=\mu kT\) where \(\mu\) is the mobility, i.e., the coefficient that relates force to velocity in the over-damped limit. We further express the force as the negative spatial derivative of the energy. In analogy to our treatment of diffusion limited reaction where \(E(x)=0\), we look for a state solution with constant flux -- the flux into the absorbing boundary will correspond to the rate of reaction of A and B to C. This simplifies the equation for \(P(x)\) to
$$ j = \mu kT \frac{dP(x)}{dx} - \mu\frac{d E}{dx} P(x)$$
If the energy barrier is high, the flux will be small and to a first approximation we can ignore the flux \(j\) far from the barrier where \(P(x)\) is large. In this case, we get
$$ P(x) = ce^{-(E(x) - E(\infty)/kT}$$
where \(c\) is the concentration of the molecule pair at long distances. This solution is identical to the equilibrium Boltzmann distribution. However, it does not hold at or even in the vicinity of the energy barrier (it predicts the density to increase after crossing the barrier, but that is where the absorbing boundary sits). What this approximate solution implies is that the energy barrier acts as an approximate reflecting boundary. Now for convenience assume the energy barrier is exactly at \(x=0\) and lets approximate the energy barrier locally as a parabola \(E(x) = E_b - ax^2/2\). This simplifies the problem
$$ \frac{dP(x)}{dx} = \frac{j}{\mu kT} + \frac{ax}{kT} P(x)$$
This equation has the solution
$$ P(x) = e^{\frac{ax^2}{2kT}} \frac{j}{\mu kT}\int_{x_0}^{x} e^{-\frac{ay^2}{2kT}} dy$$
where lower integration boundary can be chosen to fulfill the boundary condition \(P(x)\to 0\) at large positive \(x\). Hence the upper boundary needs to be \(x_0=\infty\) and we can write the solution as
$$ P(x) = - \frac{j}{\mu kT}e^{\frac{ax^2}{2kT}}\int_{x}^{\infty} e^{-\frac{ay^2}{2kT}} dy$$
This solution if valid in the vicinity of the barrier and a few times \(\sqrt{kT/a}\). We have to match this solution to the quasi-equilibrium solution far from the barrier. To this end, remember that \(\int_{-\infty}^{\infty} e^{-\frac{ay^2}{2kT}} = \sqrt{\frac{2\pi kT}{a}}\) such that we arrive at the condition
$$ j/\mu e^{ax^2/kT} \sqrt{\frac{2\pi}{a kT}} = c e^{-(E(x) - E_b+\Delta E)/kT} $$
where we have replaced \(E_{\infty}\) by \(E_b-\Delta E\), i.e., the peak minus the barrier height. Now \(E(x)-E_b\approx - ax^2/2\) such that the flux is
$$ j = \mu c \sqrt{\frac{a kT}{2\pi}}e^{-E_b/kT} = D c \sqrt{\frac{a}{2\pi kT}}e^{-E_b/kT}$$
As expected, the rate is linear in the diffusion coefficient and the concentration and it depends exponentially on the height of the energy barrier. In addition, we see that the rate depends also on the shape of the energy landscape near the transition state. The sharper this peak is (larger \(a\)), the more rapid is the transition.
So when are the approximations we made good approximations? First, we assumed that \(j\) is small compared to \(D P'\) and \(\mu E'P\). The flux \(j\sim D c e^{-E_b/kT}\). Hence this approximation is good where ever \(E(x)-E_{\infty}\ll E_b\). Since this dependence is exponential, we don't really need a big difference in these two numbers: The approximation should be accurate to about 1% outside of 4kT of the barrier. The other approximation we have made is the parabolic approximation of the barrier. Every peak, to first order, is a parabola. And we only need this approximation to be good within a few kT of the peak -- until we match it with the equilibrium solution.
The method of dominant balance
We have calculated the rate of barrier crossing -- central to reaction rates or any processes that require overcoming of an activation energy by thermal fluctuations -- by matching two solutions that are accurate before and on the barrier. The solution before the barrier was obtained by ignoring the flux, the part on the barrier by approximating the potential, and the we could calculate a simple solution of the right of the barrier. Key to solving problems like this is to know what to ignore -- a concept central to the method of the dominant balance. We have used this method approximating when we ignored the flux.
Michael Brenner in his course illustrates the power of the method of the dominant balance by finding approximate solutions to random polynomial equations. Consider
$$ 18x^5- 60x^3 + x^2/5 = 8 $$
This equation has 5 solutions, some of which might be imaginary. To proceed, one should first try to non-dimensionalize the system. Here, lets simply divide by the coefficient of the largest monomial.
$$ x^5 - 10x^3/3 + x^2/90 - 8/18 = 0 $$
The solutions at large absolute \(x\) are probably obtained when balancing the two highest monomials \(x^5 = 10x^3/3\) corresponding to \(x_{1/2} \approx \sqrt{10/3}\approx \pm 1.82\). Plugging these solution into the equation justifies the omission of the other terms.
At small \(x\), the lowest monomials and the constant tend to contribute. In this case the cubic component has a large prefactor, so we might want to try \(\frac{10}{3}x^3 = 8/18\) which corresponds to \(x_3 \approx -0.5\). Again, this is readily verified to be within a few percent of the correct solution.
Assignments
-
Simulate barrier crossing of diffusing particles across potential $$ E(x)/kT = 10e^{x - e^{x}} $$ Place a reflecting boundary at -10 and an absorbing boundary at +1 and start with a particle at \(x=-5\). Update the position of the particle by $$ x(t+\Delta t) = x(t) - \Delta t\frac{dE}{dx} + \sqrt{\Delta t}\eta $$ where \(\eta\) is a Gaussian random variable. Repeat this until the particle escaped at \(x=1\). If the particle passes through the reflecting boundary, mirror the trajectory forward. Periodically report the position of the particle and finally compare the resulting distribution to the Boltzmann distribution. Repeat the entire escape process a few hundred times (lower the barrier if it takes to long) and plot the distribution of escape times.
-
Make up a polynomial equation of 5th order with at least 4 terms and find approximate solutions.