Many biochemical reactions happen at extreme fidelity: DNA replication in some organisms makes fewer than one mistake in \(10^{10}\) bases copied. This fidelity relies on energetic discrimination the correct and wrong base pairing and that fact that extremely high accuracies can be achieved is remarkable.
However, mutation rates vary greatly across organisms: the smaller the genome, the higher the mutation rate. This anti-correlation is shown in schematically in the plot below.
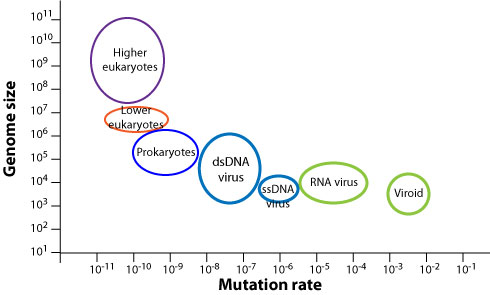
viralzone.expasy.org
Why should we expect such an anti-correlation? The probability that that the entire genome of length \(L\) is copied faithfully is given by \(exp(-L\mu)\). Hence as soon as the mutation rate is much larger than the inverse genome size, almost every new genome will contain mutations resulting in a gradual loss of functional sequence (a process known as Muller's ratchet). If being accurate is costly in terms of energy amd/or time, you'd expect organisms to adjust fidelity to be just "good enough". Hence the scaling behavior of fidelity with genome length is plausible.
However, it is not at all a trivial question how high fidelity can be achieved given the small free energy differences associated with nucleotide mis-incorporation. It was John Hopfield and Jaques Ninio who first discussed mechanisms on how to achieve high fidelity in biochemical processes. Fidelity is not only important in DNA replication, but also in translation, tRNA charging and signaling processes.
Energies of discrimination
Consider the following simple set of reactions $$ C + c \leftrightarrow Cc \rightarrow \mathrm{correct} $$ $$ D + c \leftrightarrow Dc \rightarrow \mathrm{wrong} $$ The transition states Cc and Dc are populated according to the equilibrium constant of these reactions \(K_C =k_C'/k_C\) and \(K_D = k_D'/k_D\). We assume that the product formation happens at the same rate \(W\) for both the correct and incorrect transition state. In other words, the discrimination between the wrong and the correct state happens in the formation of the transition state. This is a sensible assumption in cases like polymerization reactions which can occur as long as the two entities are in place. Furthermore, it is reasonable to assume that the on-rates \(k_C'\) and \(k_D'\) are similar since they are likely dominated by diffusion. The off-rates, on the other hand, are strongly dependent on the correct substrate match and this is where discrimination comes from. Assuming that both on-rates are \(k = k_C' = k_D'\), we can express the rate at which each product is formed as $$ W[Cc] = W\frac{k[C]}{k_C+W} $$ $$ W[Dc] = W\frac{k[D]}{k_D+W} $$ and hence the ratio of correct to wrong product is $$ \frac{\mathrm{correct}}{\mathrm{wrong}} = \frac{[C]}{[D]}\frac{k_D+W}{k_C + W} \rightarrow \frac{[C]}{[D]}\frac{k_D}{k_C} = \frac{[C]}{[D]}e^{-\Delta G/kT} $$ Here the last two expressions assumed that the product formation rate \(W\) is much smaller than the off-rates of the transition state. The very last equality expressed the off-rate dependence in terms of the difference in free energy of the transition states and thereby defines the energy of discrimination. Hence in any off-rate dominated discrimination, the differences in free energy put an upper bound on the accuracy of the process. However, the binding energy differences of incorrect nucleotide reactions are on the order of a few kT and while accuracy of DNA replication would seem to require energies of discrimination on the order of 20kT. This conundrum is what kinetic proofreading resolves in an elegant way.
Irreversible intermediate states and kinetic proof reading
Kinetic proof reading requires additional steps in the pathway to final product, but at least one of these steps needs to be coupled to an additional energy consuming reaction that makes the pathway irreversible. The need for such an additional step is seen as follows: A reaction that proceeds via two intermediate states \(Xc\) and \(Xc'\) can effectively be compressed into one $$ X + c \leftrightarrow Xc \leftrightarrow Xc' \rightarrow \mathrm{product} $$ $$ X + c \leftrightarrow Xc' \rightarrow \mathrm{product} $$ or put otherwise the second intermediate state is in equilibrium with the same discriminatory ratio as before.
If, however, the transition from \(Xc\) to \(Xc' \) is coupled to an irreversible reaction while \(Xc' \) can still decay into \(X+c\), higher accuracy can be attained. In this case, the state \(Xc' \) can only be reached via \(Xc\) which is already selected for the correct product by a factor \(e^{-\Delta G/kT}\). If the rates of decay of \(Xc' \) for C and D are again different by a factor \(e^{-\Delta G/kT}\), the overall accurary of the process can be as high as \(e^{-2\Delta G/kT}\).
The accuracy of a process can be exponentiated by adding more and more intermediate states.
Interpretation of proof-reading as a delay
The addition of an irreversible step essentially changes the distribution of times the product spends in the transition state. While being in the transition state, the correct pair decays as \(e^{-k_Ct}\) and the wrong product as \(e^{-k_Dt}\) such that the ratio behaves as \(e^{-(k_C-k_D)t}\). In a one step reaction, the distribution of residence times in the transition state has a peak at \(t=0\) and decays exponentially. In a two-step reaction, this distributions has a peak away from zero. This can be seen as follows. Consider the a transition state \(Xc\) the moment it is formed. The probability \(p(t)\) of still being intact is given by $$ \frac{dp}{dt} = - (k_X + W)p(t) \quad \Rightarrow\quad p(t) = e^{-(k_X+W)t} $$ where \(W\) is the rate at which the second intermediate is formed. The probability \(q(t)\) of being in the second intermediate is then $$ \frac{dq}{dt} = Wp(t) - Vq(t) = We^{-(k_X+W)t} - Vq(t) $$ The latter has the solution $$ q(t) = We^{-Vt}\int_0^t e^{(V-W-k_X)t'} dt' = \frac{We^{-Vt}}{W+k_X-V}\left[1-e^{-(W+k_X - V)t}\right] $$ While in a single step reaction the product starts being formed immediately, product formation starts gradually in a two step reaction. This delay give the wrong intermediate complexes more time to break up and hence better discrimination.
Phase transitions and percolation
In the next session, we will consider phase transitions in cell biology. Before we get there, it is useful to consider simple models of phase transitions that highlight some of the phenomena that we will encounter. Consider a polymer melt (a dense solution of polymers) and start adding cross-links between the polymers. With increasing number of cross-links, the system will go from a liquid to a gel which resists shear force. These cross-links could be covalent bonds, base-pairings, protein-crosslinks etc. Examples of this process abound for example in industrial applications or cooking.
Such a sol-gel transition has very intruiging features: The properties of the material change suddenly at a well defined density of cross-links. In the vicinity of the transition, the systems exhibits a number of universal properties that do not depend on the microscopic features of the system. The simplest mathematical model to appreciate this behavior is percolation on a so called Bethe lattice. Assume that each molecule \(z\) potential neighbors and that each pair of neigbors is cross-linked with probability \(p\). Furthermore, assume that there are no loops in the graph, i.e. that none of your neighbors are connected to each other (this is a strong approximation, but it will make the calculation is lot simpler). Let's call the probability that the molecule is not connected to the infinite connected component via a particular link \(Q = 1-P\). For the monomer not to be connected to infinite component via a particular link is
$$ Q = (1-p) + pQ^{z-1}$$
The first term accounts for the bond not being formed, while the second term corresponds to the bond being in place but none of the \(z-1\) other neighbors making a connection to the infinite component. Our monomer in question has \(z\) neighbors. Hence its probability not to be connected is \(P = Q^{z}\).
What solutions does the above equation have? For \(z=2\), it is clear that the only solution is \(Q=1\) unless \(p=1\). This is intuitively clear: there is no possibilty of making an infinite component with stochastically linking neighbors in one dimension. But for any \(z>2\), there is a non-trivial solution.
Consider \(z=3\) first. In this case, we are left with a quadratic equation for \(Q\)
$$ Q = (1-p) + pQ^2 \quad \Rightarrow\quad Q = \frac{1}{2p} \pm \sqrt{\frac{1}{4p^2} - \frac{1-p}{p}} = 1, \frac{1-p}{p}$$
The interesting solution is \(P = Q^3 = \left(\frac{1-p}{p}\right)^3\). This is larger than 1 for \(p<1/2\), which is obviously non-sensical. Put for larger \(p\), this solution is relevant. At \(p_c=0.5\), the fraction of monomers that are part of the giant component goes from strictly zero to a positive value and increases a \(p\) increases. In this simple model, the critical point is in fact always at \(p_c = \frac{1}{z-1}\).
Two dimensional site percolation
The Bethe lattice discussed above has essentially infinite dimension. Analyzing percolation problems is both more difficult and more relevant in dimensions 2 and 3. The pecularities of two dimensions mean that many properties of are understood analytically, but still numerical analysis is key to explore such problems.
Simple animation illustrating site percolation